最近使用到了OOQP求解凸优化问题，所以记录一下求解简单的二次凸优化问题。

目录

一、OOQP安装

二、OOQP相关介绍

三、例题

1.数学例题

2.代码求解

3.求解结果

总结

一、OOQP安装

参考了浙大高飞老师团队提供的 OOQP 的安装步骤，其参考链接如下：

Teach-Repeat-Replan/onboard_computer/controller/n3ctrl at experiment · HKUST-Aerial-Robotics/Teach-Repeat-Replan · GitHub

二、OOQP相关介绍

OOQP的介绍文档如下，不过是全英的，看起来可能稍微有点不爽，但是勉强可以理解。

https://pages.cs.wisc.edu/~swright/ooqp/ooqp-userguide.pdf

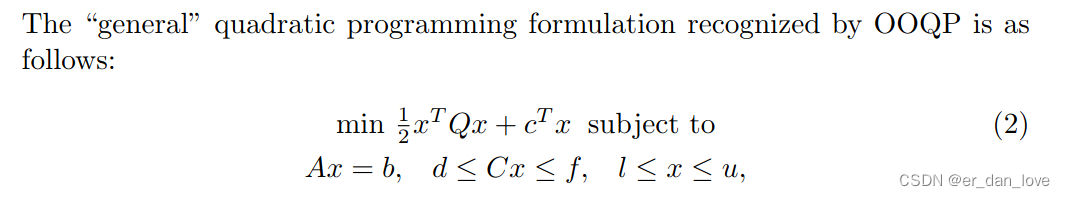
其中参数的介绍也有详细的说明。这里也可以参考这位博主的文章有对相关参数的详细介绍：

2021-08-31_流川_phone的博客-CSDN博客_ooqp求解器

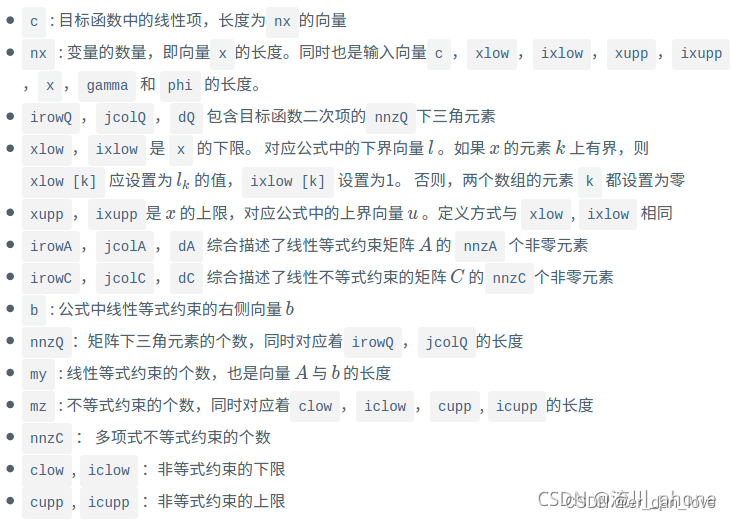
三、不等式约束例题

1.参数提取

从上式中可以提取出，，。x的取值范围是负无穷到正无穷。到这儿就提取出了这几个主要的矩阵参数信息。

2.代码求解

代码如下：

#include "ooqp/QpGenData.h"
#include "ooqp/QpGenVars.h"
#include "ooqp/QpGenResiduals.h"
#include "ooqp/GondzioSolver.h"
#include "ooqp/QpGenSparseMa27.h"

#include <iostream>
#include <string.h>

using namespace std;

const int nx = 2;
double c[] = {-2,-6};
double xupp[] = {0,0};
char ixupp[] = {0,0};

double xlow[] = {0,0};
char ixlow[] = {0,0};

const int nnzQ = 3;
int irowQ[] = {0,1,1};
int jcolQ[] = {0,0,1};
double dQ[] = {1,-1,2};

int my = 0;//线性等式约束的个数
double *b = 0;
int nnzA = 0;
int *irowA = 0;
int *jcolA = 0;
double *dA = 0;

const int mz = 3;
double clow[] = {0,0,0};
char iclow[] = {1,1,1};

double cupp[] = {2,2,3};
char icupp[] = {1,1,1};

const int nnzC = 6;
int irowC[] = {0,0,1,1,2,2};
int jcolC[] = {0,1,0,1,0,1};
double dC[] = {1,1,-1,2,2,1};

int main(int argc,char * argv[])
{
	int usage_ok = 1;
	int quiet = 0;
	if(argc > 2)
	{
		usage_ok = 0;
	}
	if(argc == 2)
	{
		if(0 == strcmp("--quiet",argv[1]))
		{
			quiet = 1;
		}
		else
		{
			usage_ok = 0;
		}
	}	

	if(!usage_ok)
	{
		cerr<<"Usage:"<<argv[0]<<"[--quiet]"<<endl;
		return 1;
	}
	QpGenSparseMa27 * qp = new QpGenSparseMa27(nx,my,mz,nnzQ,nnzA,nnzC);
	QpGenData * prob = (QpGenData *)qp -> copyDataFromSparseTriple(
			c,irowQ,nnzQ,jcolQ,dQ,
			xlow,ixlow,xupp,ixupp,
			irowA,nnzA,jcolA,dA,b,
			irowC,nnzC,jcolC,dC,
			clow,iclow,cupp,icupp);
	QpGenVars * vars = (QpGenVars *)qp -> makeVariables(prob);
	QpGenResiduals *resid = (QpGenResiduals *)qp -> makeResiduals(prob);

	GondzioSolver *s = new GondzioSolver(qp,prob);
	
	if(!quiet)
	{
		s->monitorSelf();
	}
	int ierr = s->solve(prob,vars,resid);

	if(ierr == 0)
	{
		cout.precision(4);
		cout<<"Solution:"<<endl;
		vars->x->writefToStream(cout,"x[%{index}] = %{value}");
	}
	else
	{
		cout<<"Could not solve the problem!"<<endl;
	}

	return ierr;
}

3.求解结果

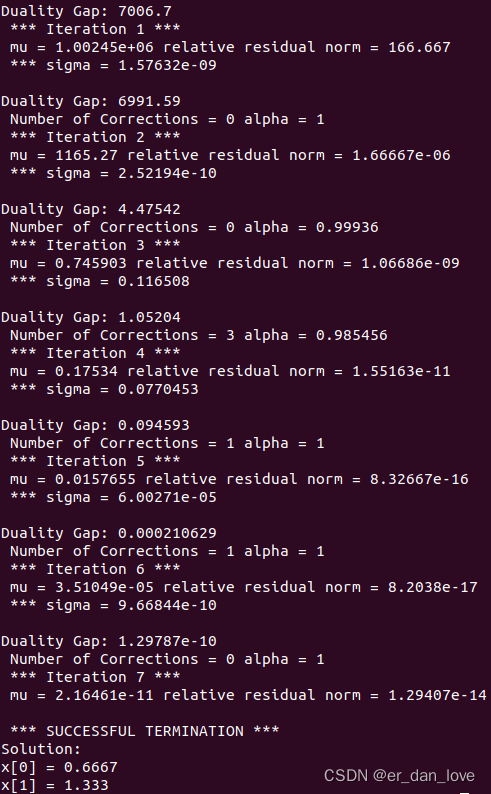
从上图中可以看出变量的取值分别为 0.6667 和 1.333。

四、等式约束例题

1、参数提取

最小化的目标函数同上一部分所介绍的目标函数是一样的，不同的是这个只有等式约束没有不等式约束，需要修改的是这一部分，如下图所示。

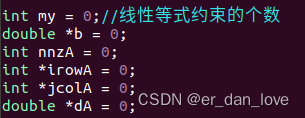
这里线性等式约束只有一个故需要修改，b 的值是等式约束右侧的值，nnzA 是等式约束左侧系数矩阵中的下三角元素个数，irowA 和 jcolA 分别为元素对应的角标都是从 0 开始的，dA 代表等式约束中系数矩阵的元素的值。其余部分和上面那部分的代码相同。

2、代码求解

#include "ooqp/QpGenData.h"
#include "ooqp/QpGenVars.h"
#include "ooqp/QpGenResiduals.h"
#include "ooqp/GondzioSolver.h"
#include "ooqp/QpGenSparseMa27.h"

#include <iostream>
#include <string.h>

using namespace std;

const int nx = 2;
double c[] = {-2,-6};

double xupp[] = {0,0};
char ixupp[] = {0,0};

double xlow[] = {0,0};
char ixlow[] = {0,0};

const int nnzQ = 3;
int irowQ[] = {0,1,1};
int jcolQ[] = {0,0,1};
double dQ[] = {1,-1,2};


int my = 1;//线性等式约束的个数
double b[] = {0};
int nnzA = 1;
int irowA[] = {0,0};
int jcolA[] = {0,1};
double dA[] = {1,1};

const int mz = 0;
double *clow = 0;
char *iclow = 0;
double *cupp = 0;
char *icupp = 0;

const int nnzC = 0;
int *irowC = 0;
int *jcolC = 0;
double *dC = 0;

int main(int argc,char * argv[])
{
	int usage_ok = 1;
	int quiet = 0;
	if(argc > 2)
	{
		usage_ok = 0;
	}
	if(argc == 2)
	{
		if(0 == strcmp("--quiet",argv[1]))
		{
			quiet = 1;
		}
		else
		{
			usage_ok = 0;
		}
	}	

	if(!usage_ok)
	{
		cerr<<"Usage:"<<argv[0]<<"[--quiet]"<<endl;
		return 1;
	}
	QpGenSparseMa27 * qp = new QpGenSparseMa27(nx,my,mz,nnzQ,nnzA,nnzC);
	QpGenData * prob = (QpGenData *)qp -> copyDataFromSparseTriple(
			c,irowQ,nnzQ,jcolQ,dQ,
			xlow,ixlow,xupp,ixupp,
			irowA,nnzA,jcolA,dA,b,
			irowC,nnzC,jcolC,dC,
			clow,iclow,cupp,icupp);
	QpGenVars * vars = (QpGenVars *)qp -> makeVariables(prob);
	QpGenResiduals *resid = (QpGenResiduals *)qp -> makeResiduals(prob);

	GondzioSolver *s = new GondzioSolver(qp,prob);
	
	if(!quiet)
	{
		s->monitorSelf();
	}
	int ierr = s->solve(prob,vars,resid);

	if(ierr == 0)
	{
		cout.precision(4);
		cout<<"Solution:"<<endl;
		vars->x->writefToStream(cout,"x[%{index}] = %{value}");
	}
	else
	{
		cout<<"Could not solve the problem!"<<endl;
	}

	return ierr;
}

三、求解结果

从求解结果中可以得出 x1 和 x2 值分别是 0 和 3。

总结

以上就是OOQP的安装以及使用OOQP对简单的二次凸优化问题进行求解的过程。