最小生成树--Prim算法（Python）

1、Prim算法原理
Prim算法在找当前最近顶点时使用到了贪婪算法。Prim算法从任意一个顶点开始，每次选择一个与当前顶点集最近的一个顶点，并将两顶点之间的边加入到树中,直到当前顶点集顶点个数为n或者树中边数为n-1。
2、实战演练
下面给出一个无向图G=（V，E），我们使用Prim算法来找它的最小生成树。
第一步，我们先随意选择一个顶点作为起始点（起始点的选取不会影响最小生成树结果），在此我们一般选择v1作为起始点，现在我们设当前所找到最小生成树里面的顶点为集合V’，所找到的边为集合E’。初始状态如下：V’={v1}； E’={}。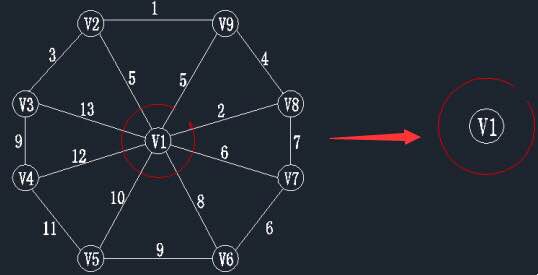

第二步，查找顶点在V’ ={v1}，V-V’ 集合中的最小权值，如下图，在红线相交的线上找最小值。通过图中我们可以看到边（v1，v8）的权值最小为2，那么将v8加入到V’，边（v1，v8）加入到 E’。 此时状态如下：V’={v1，v8}； E’={（v1，v8）}。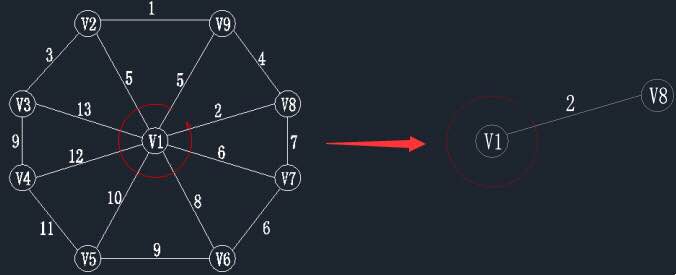

第三步，查找顶点在V’={v1，v8}，V-V’ 集合中的最小权值，如下图，在红线相交的线上找最小值。通过图中我们可以看到边（v8，v9）的权值最小为4，那么将v9加入到V’，边（v8，v9）加入到 E’。 此时状态如下：V’ ={v1，v8，v9}； E’={（v1，v8），（v8，v9）}。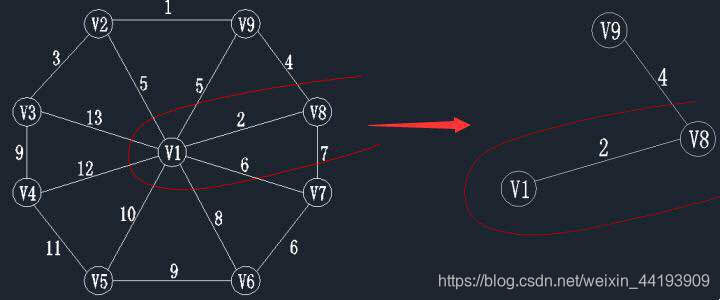

第四步，查找顶点在V’ ={v1，v8，v9}，V-V’ 集合中的最小权值，如下图，在红线相交的线上找最小值。通过图中我们可以看到边（v9，v2）的权值最小为1，那么将v2加入到V’，边（v9，v2）加入到 E’。 此时状态如下：V’={v1，v8，v9，v2}； E’={（v1，v8），（v8，v9），（v9，v2）}。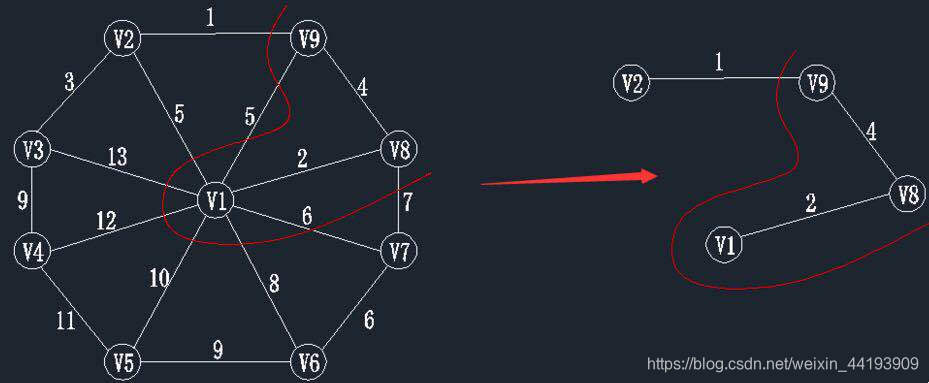

以此类推，直到找到所有顶点为止，最后得到无向图G的最小生成树MST=（V’，E’），如下图所示：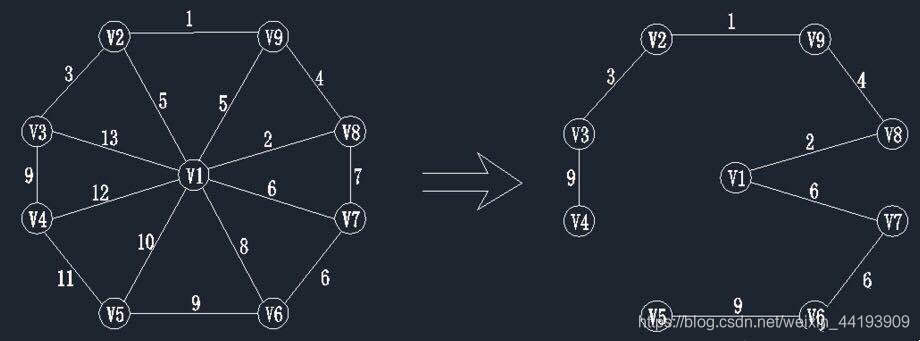

3、Python实现

#Prim algorithm(python)
from collections import defaultdict
from heapq import heapify, heappush, heappop
import time
start = time.perf_counter()
def Prim(nodes, edges):
    '''  基于最小堆实现的Prim算法  '''
    element = defaultdict(list)
    for start, stop, weight in edges:
        element[start].append((weight, start, stop))
        element[stop].append((weight, stop, start))
    all_nodes = set(nodes)
    used_nodes = set(nodes[0])
    usable_edges = element[nodes[0]][:]
    heapify(usable_edges)
    # 建立最小堆
    MST = []
    while usable_edges and (all_nodes - used_nodes):
        weight, start, stop = heappop(usable_edges)
        if stop not in used_nodes:
            used_nodes.add(stop)
            MST.append((start, stop, weight))
            for member in element[stop]:
                if member[2] not in used_nodes:
                    heappush(usable_edges, member)

    return MST

def main():
    nodes = list('123456789')
    edges = [("1", "2", 5), ("1", "3",13),("1", "4",12), ("1", "5",10),
                   ("1", "6", 8), ("1", "7", 6),("1", "8", 2), ("1", "9", 5),
                   ("2", "3", 3), ("2", "9", 1),("3", "4", 9), ("4", "5",11),
                   ("5", "6", 9), ("6", "7", 6),("7", "8", 7), ("8", "9", 4)]
    print("\n\nThe undirected graph is :", edges)
    print("\n\nThe minimum spanning tree by Prim is : ")
    print(Prim(nodes, edges))

if __name__ == '__main__':
    main()
end = time.perf_counter()
print('Running time: %f seconds'%(end-start))