以斐波那契数列为例分析递归算法的时间复杂度和空间复杂度

首先来波概念：

   递归算法的时间复杂度：递归的总次数*每次递归的数量。

   递归算法的空间复杂度：递归的深度*每次递归创建变量的个数。

  那什么是斐波那契额数列呢？对于菲波那切数列有典型的生兔子的的问题，在这我就不多说了，感兴趣的同学可以自行查找资料来了解，简单的说，菲波那切数列数列就是前两项是1，后面的每项是其前两项之和。比如：1 1 2 3 5 8 13....

   下边我们来分别用不同的方法来求一下斐波那契。

（1）首先采用递归的方法来求一下：

#define _CRT_SECURE_NO_WARNINGS
 #include<stdio.h>
int Fib(int n){if (n < 3)
{
return 1;
}else{
return Fib(n - 1) + Fib(n - 2);
}}int main()
{int n = 50;int ret = Fib(n);printf("%d\n", ret);getchar();
}

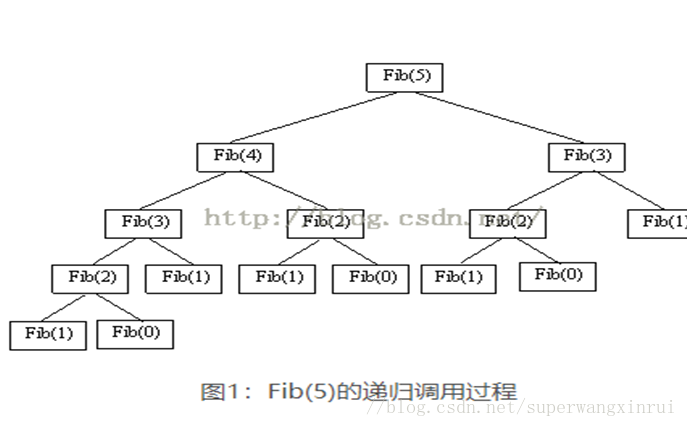
在递归调用过程中Fib(3)被计算了2次，Fib(2)被计算了3次。Fib(1)被调用了5次，Fib(0)中被调用了3次。所以，递归的效率低下，但优点是代码简单，容易理解。

 递归算法时间复杂度为(二叉树的节点个数）：O()=(2^h)-1=2^n。空间复杂度为树的高度：h即o(n).

（2）可用尾递归方法来求，尾递归若优化，空间复杂度可达到o(1)，但时间复杂度是o(n);

#define _CRT_SECURE_NO_WARNINGS 
#include<stdio.h>
long Fib(long first, long second, long n){
	if (n < 3)
		return 1;
	if (3 == n)
	{
		return first + second;
	}
	return Fib(second, first + second, n - 1);

}
int main()
{
	int n = 5;
	int ret = Fib(1,1,5);
	printf("%d\n", ret);
	getchar();
}

(3) 采用循环结构实现。

#define _CRT_SECURE_NO_WARNINGS 
#include<stdio.h>
long Fib(long first, long second, long n){
	int third = 0;
	if (n < 3)
		return 1;
	while (n >3){
		int temp = second;
	second = first + second;
	first = temp;
	
	n--;
}
	third = first + second;
	return third;
	
}
int main()
{
	int n = 6;
	int ret = Fib(1,1,n);
	printf("%d\n", ret);
	getchar();
}

此时时间复杂度达到了o(n),空间复杂度达到了o(1).

所以综上所述，求菲波那切数列最好使用循环的方式。

最后来科普一下，常用时间复杂度所耗费的时间从小到大依次是o(1）<o(log2n)<o(n)<o(nlog2n)<o(n^2)<o(n^3)<o(2^n)<o(n!)<o(n^n).