Leetcode 1884. 鸡蛋掉落-两枚鸡蛋 (经典动态规划数学题）

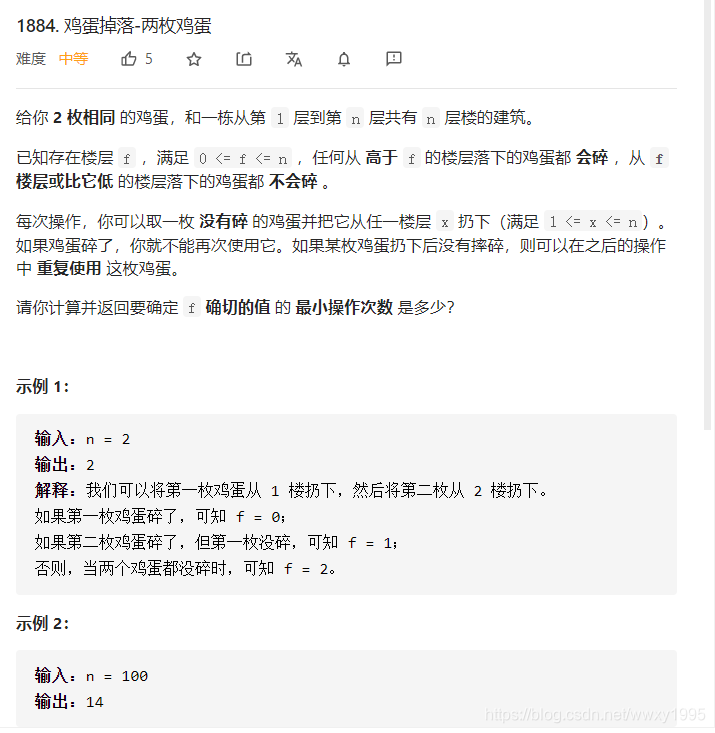
如果只有一个鸡蛋，要确定N层楼，只能从第一层确定到第N层。

对于两个鸡蛋，可以先用第一个鸡蛋，确定一个大致范围，如果第一个鸡蛋碎了，第二个鸡蛋要从第一个鸡蛋没碎的层，试到第一个鸡蛋碎了的层。

比如100层

第一个鸡蛋分别从10层，20层，30层，。。。扔到100层

如果10层碎了， 1 + 9 = 10

如果20层碎了， 2 + 9 = 11

如果100层碎了， 10 + 9 = 19次

因此这样最坏情况需要19次

如果x层碎了， 1 + x - 1 = x

x + x - 1层碎了，  2 + x - 2 = x

如果x + x - 1 + （x - 2）层碎了

用动态规划的思想解决这个问题，f[i][j] 表示j个鸡蛋，确定i层楼的最小操作次数，显然f[i][1] = i

f[i][2], 我们首先任意选取一层k，假如蛋碎了，那么只有一个蛋，还需要f[k-1][1]次，即k-1次才可以确定，如果蛋没碎，那么最少还需要f[i-k][2]。最怀情况下取max

class Solution {
public:
    int twoEggDrop(int n) {
        // f[i][j] 表示j个蛋，验证N层所需要的最小操作次数
        vector<vector<int>> f(n+1, vector<int>(3, INT_MAX));
        for(int i = 0; i <= n; i++) {
            f[i][1] = i;
        }
        f[0][2] = 0;
        for(int i = 1; i <=n; i++) {
            for(int k = 1; k <= i; k++) {
                f[i][2] = min(f[i][2], max(1 + f[i - k][2], 1 + f[k - 1][1]));
            }
        }
        return f[n][2];
    }
};