目录
1 神经网络为什么需要非线性激活函数?
首先我们来看下线性和非线性函数
线性变换函数,比如:y = 2 x y=2xy=2x y = x y =xy=x
非线性变换函数,比如:y = 2 x 2 y=2x^2y=2x2 y = c o s x y=cosxy=cosx
非线性函数是指的一阶导数不为常数的函数
如果神经网络激活函数用线性函数,则网络的输出y yy还是x xx输入的一个线性函数,则模型无法表征非线性函数的输出
比如在第一层神经元:a 1 = w 1 x + b 1 a_1=w_1x+b_1a1=w1x+b1
第二层神经元:a 2 = w 2 a 1 + b 2 = w 2 ( w 1 x + b 1 ) + b 2 a_2=w_2a_1+b_2=w_2(w_1x+b_1)+b_2a2=w2a1+b2=w2(w1x+b1)+b2
= ( w 2 w 1 ) x + ( w 2 b 1 + b 2 ) = w ′ x + b ′ =(w_2w_1)x+(w_2b_1+b_2)=w^{'}x+b^{'}=(w2w1)x+(w2b1+b2)=w′x+b′
…
y yy的输出是x xx的线性关系,线性函数的组合还是线性函数,所以网络再深,最后输出的y yy还是x xx的线性函数。所以用非线性激活函数,神经网络理论上可以逼近任意函数。
那么对于我们常见的非线性激活函数,他们各自又有什么特点和缺陷?
2 Sigmoid
数学表达式:
f ( x ) = 1 1 + e − x f(x)= \frac {1}{1+e^{-x}}f(x)=1+e−x1
函数图形:
 f ( x ) f(x)f(x)的导数数学表达式:f ( x ) ′ = f ( x ) ( 1 − f ( x ) ) f(x)^{'}=f(x)(1-f(x))f(x)′=f(x)(1−f(x))函数导数图形:
f ( x ) f(x)f(x)的导数数学表达式:f ( x ) ′ = f ( x ) ( 1 − f ( x ) ) f(x)^{'}=f(x)(1-f(x))f(x)′=f(x)(1−f(x))函数导数图形:
python实现如下:
import numpy as np
def sigmoid(x,derivative=False):
if derivative == True:
return x * (1 - x)
return 1 / (1+np.exp(-x))
2.1缺陷
2.1.1 梯度消失
我们知道f ( x ) = s i g m o i d ( x ) f(x)=sigmoid(x)f(x)=sigmoid(x)其中m a x f ( x ) ′ = 1 / 4 max f(x)^{'}=1/4maxf(x)′=1/4,根据BP算法中的链式法则,当网络很深的时候,小于1的数(1/4)累乘会趋向于0,如下图所示: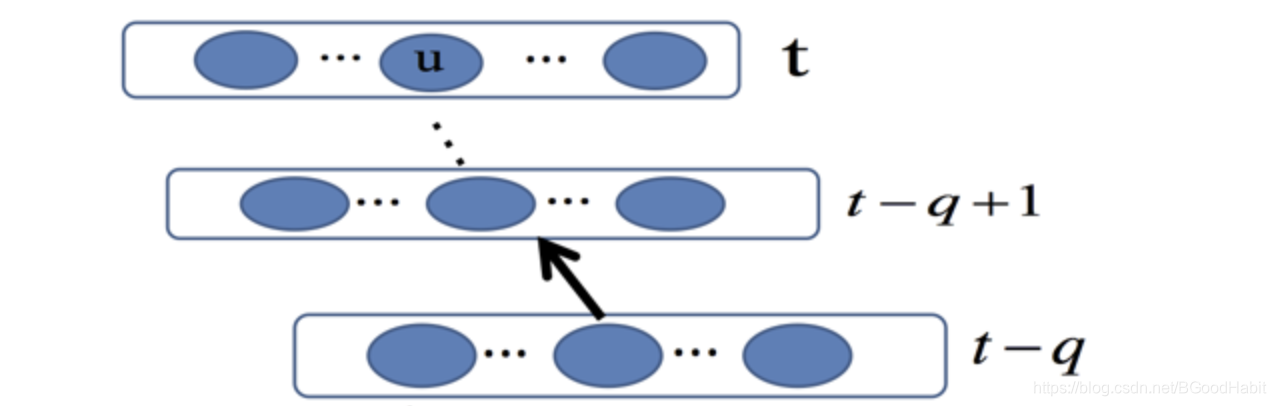
我们令θ u ( t ) \theta_u(t)θu(t)表示第t tt层神经元u uu的残差,f v ( x ) f_v(x)fv(x)表示为神经元v经过激活函数f ( x ) f(x)f(x)的输出,则有如下公式:
∂ θ v ( t − q ) ∂ θ u ( t ) = { f v ′ ( n e t v ( t − 1 ) ) w u v i f q = 1 f v ′ ( n e t v ( t − q ) ) ∑ l = 1 n ∂ θ l ( t − q + 1 ) ∂ θ ( t ) w l v e l s e \frac{\partial\theta_v(t-q)}{\partial\theta_u(t)}=\begin{cases} f^{'}_v(net_v(t-1))w_{uv} \quad if \text{ }q=1 \\ f^{'}_v(net_v(t-q))\sum_{l=1}^n\frac{\partial\theta_l(t-q+1)}{\partial\theta(t)}w_{lv} \quad else \end{cases}∂θu(t)∂θv(t−q)={fv′(netv(t−1))wuvif q=1fv′(netv(t−q))∑l=1n∂θ(t)∂θl(t−q+1)wlvelse
则 ∣ ∂ θ ( t − q ) ∂ θ ( t ) ∣ = ∣ ∏ m = 1 q W F ( N e t ( t − m ) ) ∣ ≤ ( ∣ W ∣ m a x N e t { ∣ F ′ ( N e t ) ∣ } ) q \begin{vmatrix} \frac{\partial\theta(t-q)}{\partial\theta(t)}\end{vmatrix}=\begin{vmatrix}\prod_{m=1}^qWF(Net(t-m))\end{vmatrix} \le (\begin{vmatrix}W\end{vmatrix}max_{Net}\{\begin{vmatrix}F^{'}(Net)\end{vmatrix}\})^q∣∣∣∂θ(t)∂θ(t−q)∣∣∣=∣∣∏m=1qWF(Net(t−m))∣∣≤(∣∣W∣∣maxNet{∣∣F′(Net)∣∣})q
其中m a x f ′ = 1 / 4 maxf^{'}=1/4maxf′=1/4;则当∣ W ∣ < 4 \begin{vmatrix}W\end{vmatrix} < 4∣∣W∣∣<4时候,上式子将会是一个小于1的值的q qq次乘方,则模型越往前传播,梯度会越来越小,甚至接近0,出现梯度消失现象,网络中的参数没法学习更新的情况。
2.2.2 Output非zero-centered
sigmoid函数,将输出值映射到 (0,1)之间,都是正数,没有负数,这导致网络的学习表达能力将会受到限制。
3 Tanh
数学表达式:
f ( x ) = e x − e − x e x + e − x = 2 1 + e − 2 x − 1 = 2 s i g m o i d ( 2 x ) − 1 f(x)= \frac {e^x-e^{-x}} {e^x+e^{-x}} = \frac {2}{1+e^{-2x}} -1=2sigmoid(2x)-1f(x)=ex+e−xex−e−x=1+e−2x2−1=2sigmoid(2x)−1
从公式可以看出,tanh函数就是sigmoid函数的一个简单缩放,输出值在(-1,1)之间,输出是以0为中心的。
函数图形: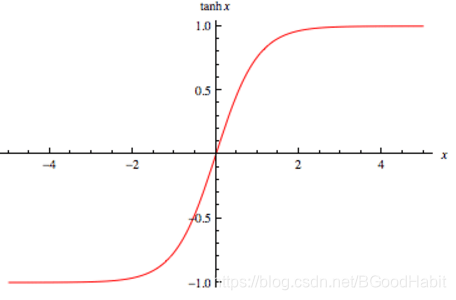
f ( x ) f(x)f(x)的导数数学表达式:
f ( x ) ′ = 1 − f ( x ) 2 f(x)^{'} = 1-f(x)^2f(x)′=1−f(x)2
函数导数图形:
python实现如下:
def tanh(x, derivative=False):
if devivative == True:
return (1 - (x ** 2))
return np.tanh(x)
3.1 缺陷
修正了sigmoid函数输出非0为中心的问题,但是还是不能解决梯度消失的问题
4 ReLu
ReLu(Rectified Linear Unit)数学表达式:
f ( x ) = m a x ( 0 , x ) f(x) = max(0,x)f(x)=max(0,x)
函数图形:
函数导数数学表达式:
f ( x ) ′ = { 1 x > 0 0 x ≤ 0 f(x)^{'} = \begin {cases} 1 \quad x>0 \\ 0 \quad x \le 0 \end {cases}f(x)′={1x>00x≤0
函数导数图形: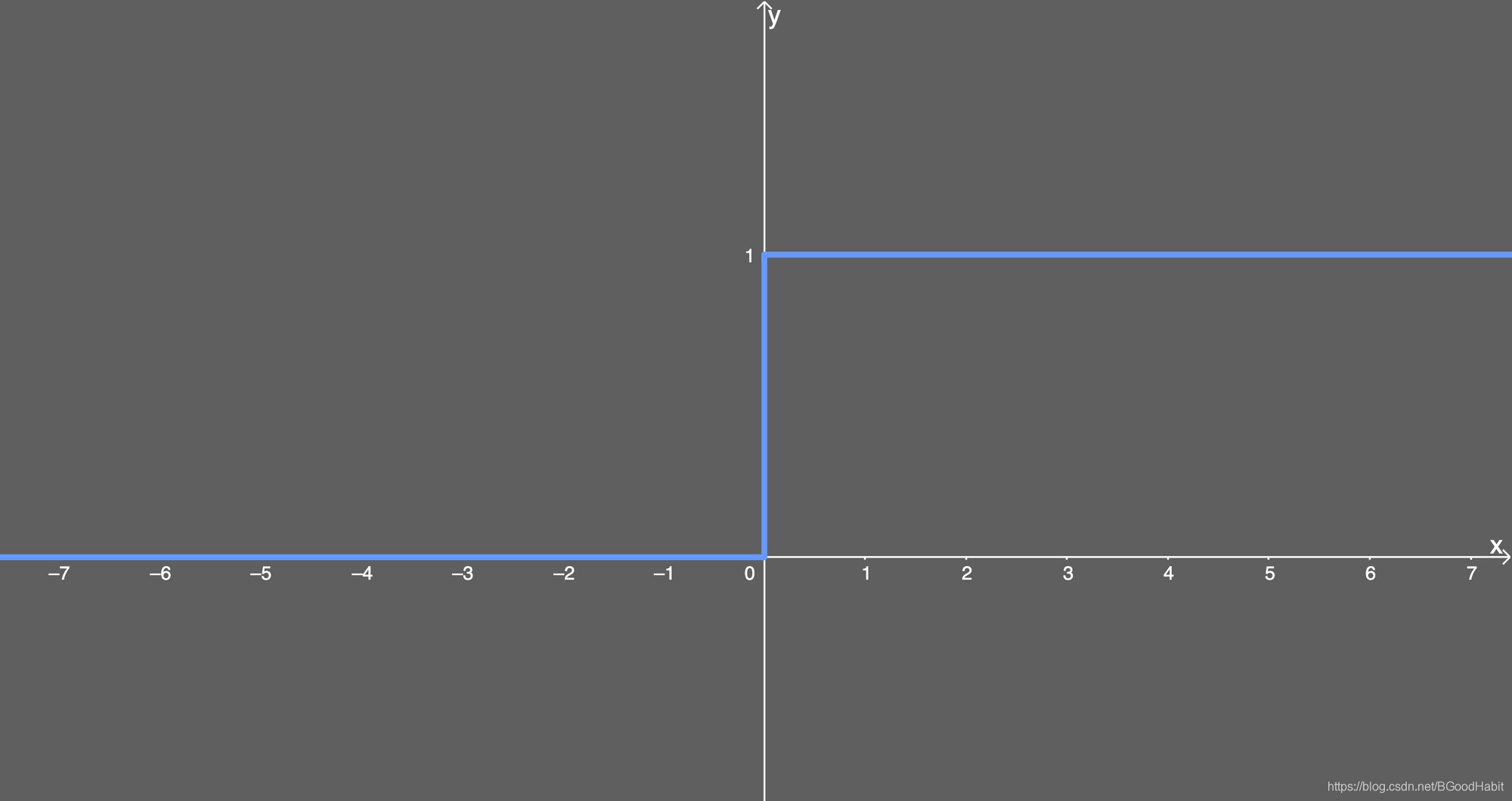
这里需要说明的一点是,ReLu是非线性函数,因为导数不是一个常数,虽然看着简单,但是ReLu函数是分段函数,组合可以逼近任意函数。
ReLu函数,时间和空间复杂度最低,也不需要更高的指数运算,而且能够缓解梯度消失问题。
4.1 缺陷
ReLu函数的一个缺陷是会引入死亡问题。什么叫“死亡问题”?
首先让我们来回顾下网络模型更新过程中的BP算法:

如上图所示,假设我们用平方和损失函数: E = 1 2 ∑ j = 1 M ( y j − t j ) 2 E = \frac {1}{2} \sum_{j=1}^{M}(y_j-t_j)^2E=21j=1∑M(yj−tj)2 其中t = { t 1 , . . . , t m } t =\{t_1,...,t_m\}t={t1,...,tm}是一个M维度的向量,代表的是每个样本的真实label标签。y j y_jyj是输出预测的第j jj个输出label值。BP反向传播更新参数梯度如下公式:
step1 :计算神经元输出值的导数
∂ E ∂ y j = y j − t j \frac {\partial E} {\partial y_j} = y_j-t_j∂yj∂E=yj−tj
step2: 计算神经元输入值的导数(通常称为“残差”)
∂ E ∂ u j = ∂ E ∂ y j . ∂ y j ∂ u j = ( y j − t j ) . f ( x ) ′ = ( y j − t j ) . y j ( 1 − y j ) = e j \frac {\partial E}{\partial u_j}=\frac {\partial E} {\partial y_j}. \frac {\partial y_j} {\partial u_j}=(y_j-t_j).f(x)^{'}=(y_j-t_j).y_j(1-y_j)= e_j∂uj∂E=∂yj∂E.∂uj∂yj=(yj−tj).f(x)′=(yj−tj).yj(1−yj)=ej
若f ( x ) f(x)f(x)为sigmoid激活函数
step3: 计算权重梯度
∂ E ∂ w i j ′ = ∂ E ∂ u j . ∂ u j ∂ w i j ′ = e j . h i \frac {\partial E}{\partial w_{ij}^{'}}=\frac {\partial E} {\partial u_j}. \frac {\partial u_j} {\partial w_{ij}^{'}}=e_j.h_i∂wij′∂E=∂uj∂E.∂wij′∂uj=ej.hi也就是第n nn层的第i ii个神经元与第n + 1 n+1n+1层的第j jj个神经元连接的权重w i j ′ w_{ij}^{'}wij′的每一次更新的梯度Δ w i j ′ \Delta w_{ij}^{'}Δwij′就是第n层的第i ii个神经元的输出值乘以第n+1层的第j jj个神经元的残差
若输入x ≤ 0 x \le 0x≤0则经过ReLu激活函数后,神经元的输出为0,所谓的“死忙问题”,那么连接的该神经元的权重梯度为0,导致权重无法更新问题,神经元处于死忙状态。
5 Leaky ReLu
Rectifier Nonlinearities Improve Neural Network Acoustic Models
数学表达式如下:
f ( x ) = { x x > 0 a x x ≤ 0 f(x)= \begin {cases} x \quad x>0 \\ ax \quad x \le 0 \end {cases}f(x)={xx>0axx≤0
函数图形如下: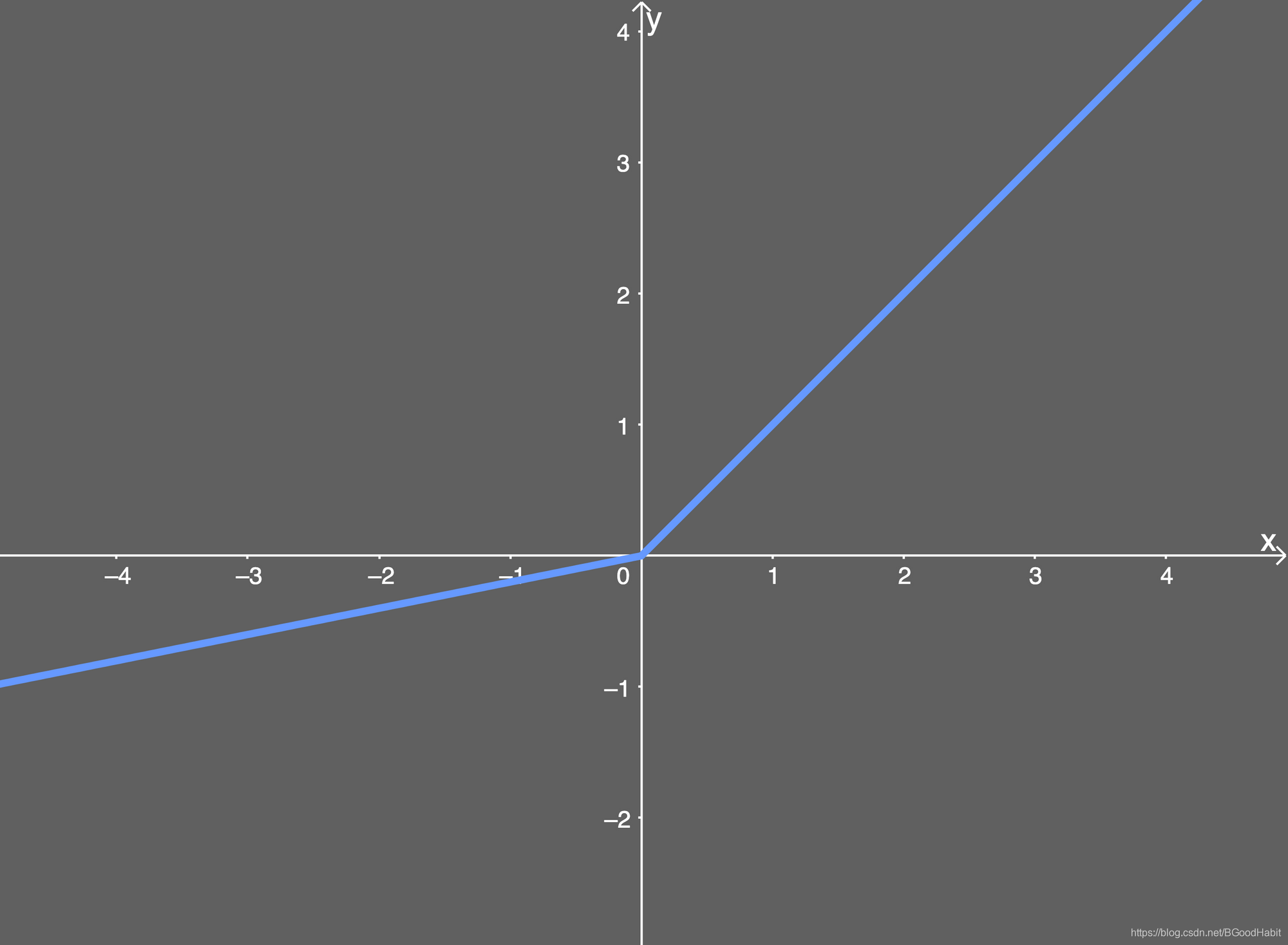
函数导数数学表达式:f ( x ) ′ = { 1 x > 0 a x ≤ 0 f(x)^{'}=\begin {cases} 1 \quad x>0 \\ a \quad x \le 0 \end {cases}f(x)′={1x>0ax≤0
图像如下: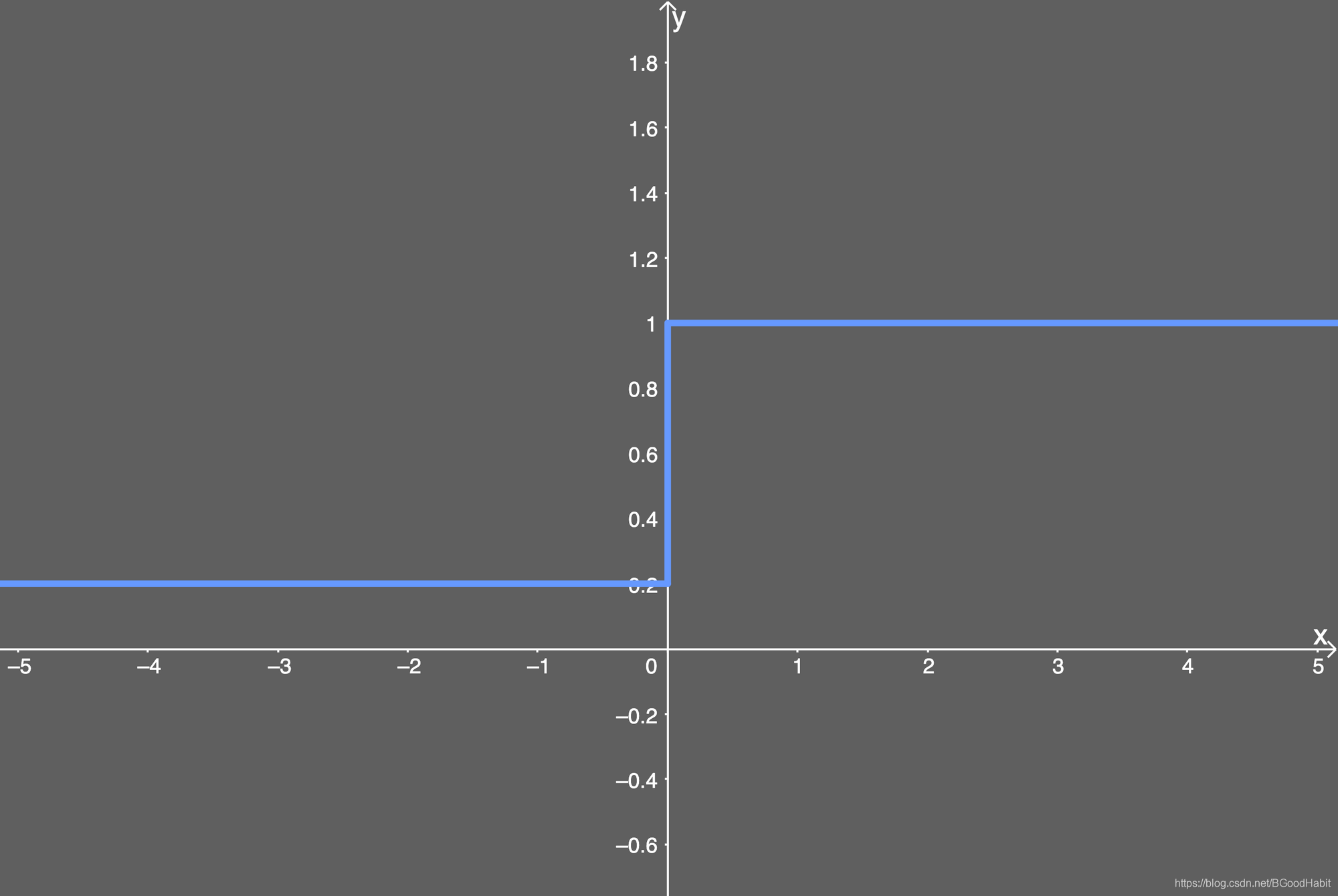
其中a aa,是一个很小的常数,避免神经元输出为0,缓解了ReLu的“死忙问题”,但是a aa是一个人工定的参数,不够灵活,所以,有一些工作,比如像Parametric ReLu把a aa当做一个参数进行训练,网络自适应学习得来。
6 ELU
FAST AND ACCURATE DEEP NETWORK LEARNING BY
EXPONENTIAL LINEAR UNITS
数学表达式:
f ( x ) = { x x > 0 a ( e x − 1 ) x ≤ 0 f(x)= \begin {cases} x \quad x>0 \\ a(e^x-1) \quad x \le 0 \end {cases}f(x)={xx>0a(ex−1)x≤0
函数图形:
导数数学表达式:
f ( x ) ′ = { 1 x > 0 a + f ( x ) x ≤ 0 f(x)^{'}= \begin {cases} 1 \quad x>0 \\ a+f(x) \quad x \le 0 \end {cases}f(x)′={1x>0a+f(x)x≤0
导数图形: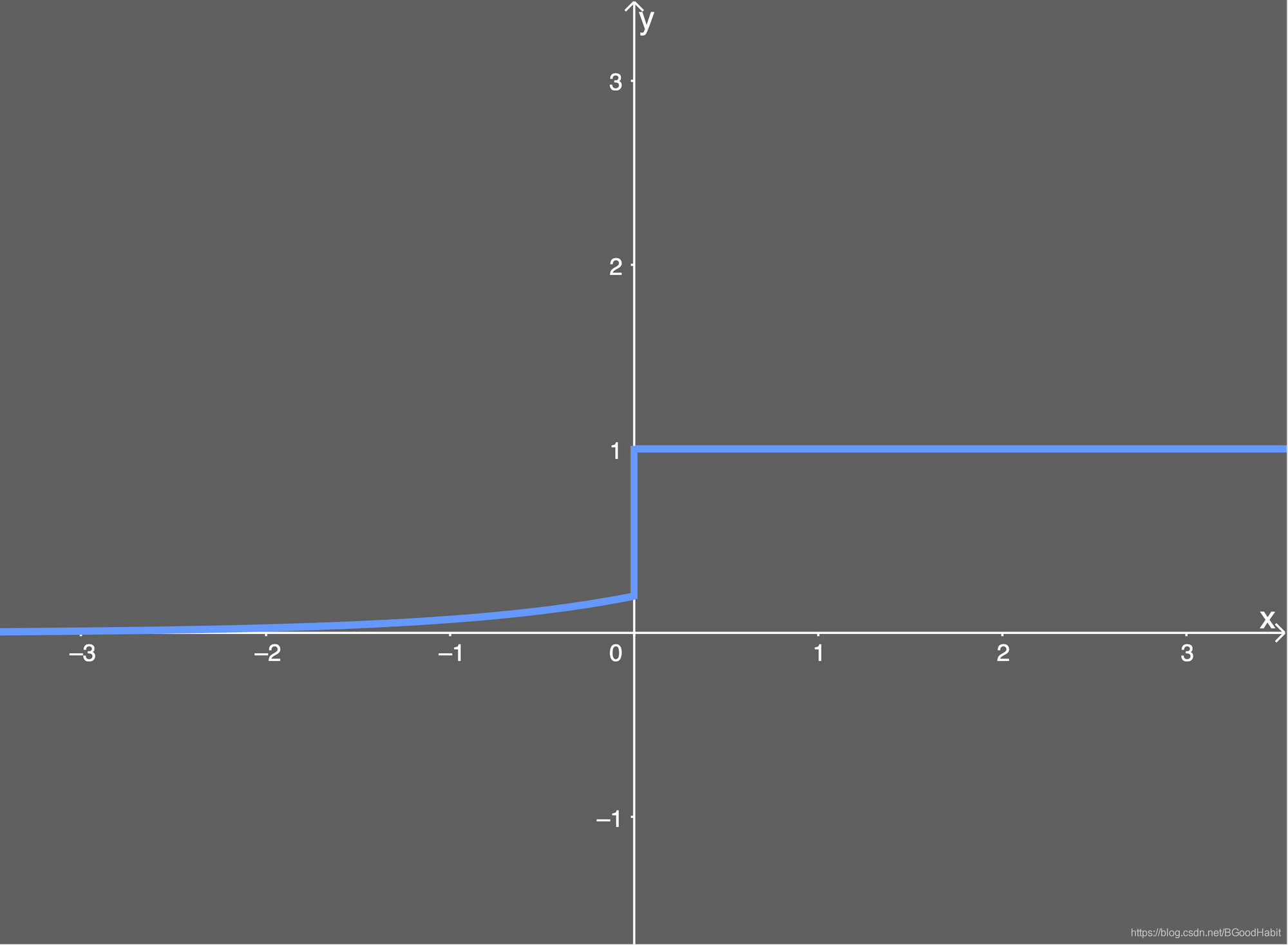
其中a aa是一个很小的常数。整体来看,Leaky ReLu,ELU以及其它的一些变体,都是在保证ReLu激活函数优势的情况下,缓解神经元"死忙"问题,从ELU公式可以看出,x xx小于0的部分,用一个指数变化形式,相对复杂一些,计算开销比Leaky ReLu要高,但输出更加平滑。
7 GeLu
7.1 基础知识回顾
7.1.1 正态分布
正态分布又名高斯分布,是一个非常常见的连续概率分布。若随机变量X XX服从一个位置参数μ \muμ、尺度参数σ \sigmaσ的正态分布,记为:X ∼ N ( μ , σ 2 ) X ∼ N(\mu,\sigma^2)X∼N(μ,σ2)则其概率密度函数为f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=σ2π1e−2σ2(x−μ)2
正态分布的数学期望值μ \muμ等于位置参数,决定了分布的位置,其方差σ 2 \sigma^2σ2的开平方或标准差σ \sigmaσ等于尺度参数,决定了分布的幅度。我们通常说的标准正态分布是位置参数μ = 0 \mu=0μ=0,尺度参数σ 2 = 1 \sigma^2=1σ2=1的正态分布,下图展示了不同μ \muμ和σ \sigmaσ的正态分布图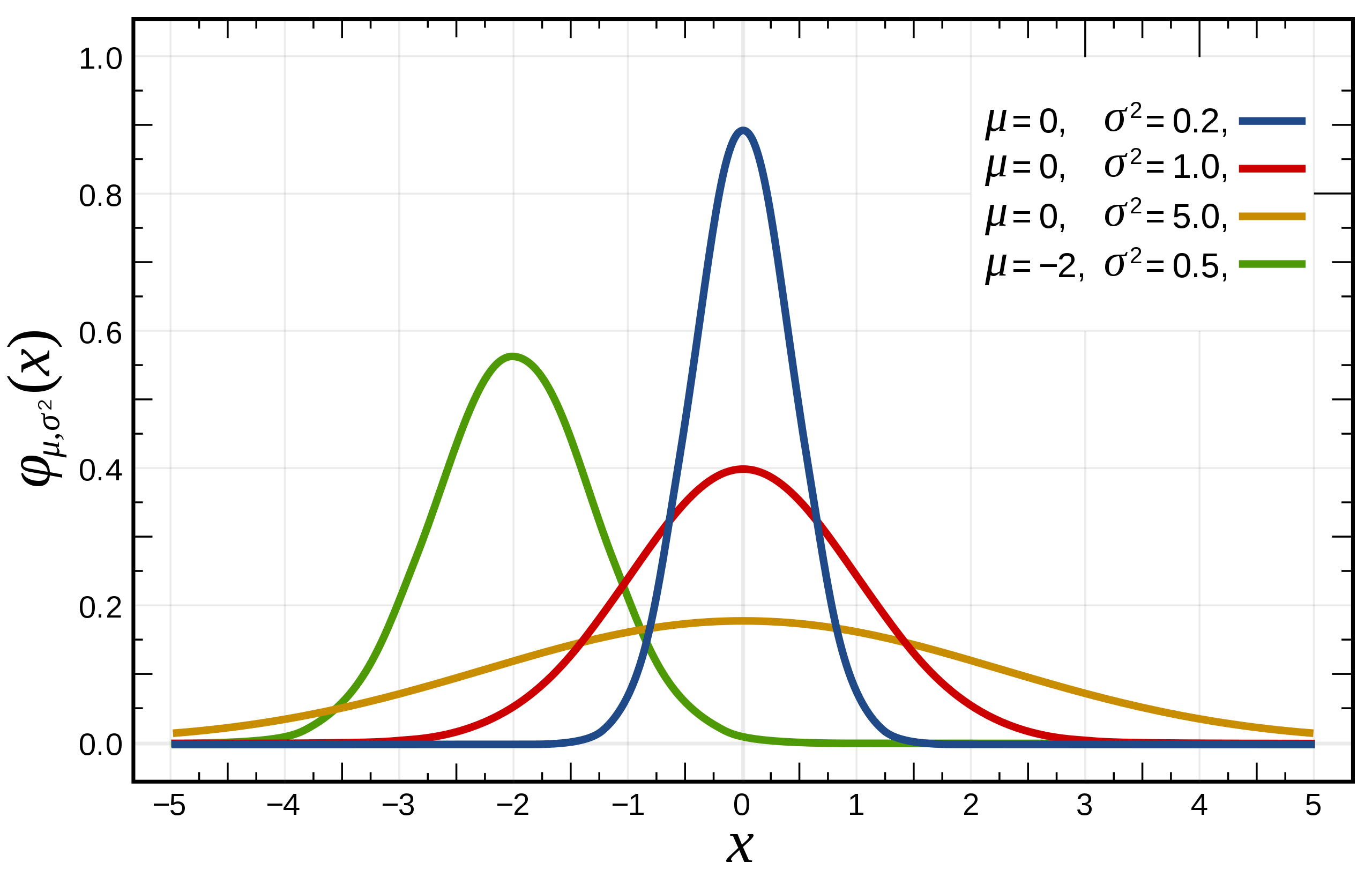
拉普拉斯在误差分析实验中使用了正态分布,勒让德于1805年引入最小二乘法这一重要方法,而高斯则宣传在1794年就使用了该方法,并通过假设误差服从正态分布。
有几种不同的方法用来说明一个随机变量,最直观的方法是概率密度函数,这种方法能够表示随机变量每个取值多大的可能性。
7.1.2 概率密度函数
正态分布的概率密度函数均值为μ \muμ,方差为σ \sigmaσ是高斯函数的一个实例:
f ( x ; μ , σ ) = 1 σ 2 π e x p ( − ( x − μ ) 2 2 σ 2 ) f(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}exp(-\frac{(x-\mu)^2}{2\sigma^2})f(x;μ,σ)=σ2π1exp(−2σ2(x−μ)2)如果一个随机变量X XX服从这个分布,我们写作X ∼ N ( μ , σ 2 ) X∼ N(\mu,\sigma^2)X∼N(μ,σ2)。如果μ = 0 \mu=0μ=0并且σ = 1 \sigma=1σ=1,这个分布被称为标准正态分布,这个分布简化为:f ( x ) = 1 2 π e x p ( − x 2 2 ) f(x)=\frac{1}{\sqrt{2\pi}}exp(-\frac{x^2}{2})f(x)=2π1exp(−2x2),下图给出了不同参数的正态分布的函数图:
7.1.3 累积分布函数
累积分布函数是指随机变量X XX小于或等于x xx的概率,用概率密度函数表示为F ( x ; μ , σ ) = 1 σ 2 π ∫ − ∞ x e x p ( − ( t − μ ) 2 2 σ 2 ) d t F(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\int^x_{-\infty} exp(-\frac{{(t-\mu)}^2}{2\sigma^2})dtF(x;μ,σ)=σ2π1∫−∞xexp(−2σ2(t−μ)2)dt
标准正态分布的累积分布函数习惯上记为Φ ΦΦ,它仅仅是μ = 0 \mu=0μ=0, σ = 1 \sigma=1σ=1时的值,
Φ ( x ) = F ( x ; 0 , 1 ) = 1 2 π ∫ − ∞ x e x p ( − t 2 2 ) d t Φ(x)=F(x;0,1)=\frac{1}{\sqrt{2\pi}}\int^x_{-\infty} exp(-\frac{{t}^2}{2})dtΦ(x)=F(x;0,1)=2π1∫−∞xexp(−2t2)dt
正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示:
Φ ( z ) = 1 2 [ 1 + e r f ( z − μ σ 2 ) ] Φ(z)=\frac{1}{2}\begin{bmatrix}1+erf(\frac{z-\mu}{\sigma\sqrt{2}}) \end{bmatrix}Φ(z)=21[1+erf(σ2z−μ)]
标准正态分布的累积分布函数习惯上记为Φ,它仅仅是指μ = 0 , σ = 1 \mu=0,\sigma=1μ=0,σ=1时的值,用误差函数表示的公式简化为:
Φ ( z ) = 1 2 [ 1 + e r f ( z 2 ) ] Φ(z)=\frac{1}{2}\begin{bmatrix}1+erf(\frac{z}{\sqrt{2}}) \end{bmatrix}Φ(z)=21[1+erf(2z)]
其中e r f ( x ) erf(x)erf(x),称为误差函数(也称为高斯误差函数),它的定义如下:
e r f ( x ) = 1 π ∫ − x x e − t 2 d t = 2 π ∫ 0 x e − t 2 d t erf(x)=\frac{1}{\sqrt\pi}\int^x_{-x}e^{-t^2}dt=\frac{2}{\sqrt\pi}\int_0^xe^{-t^2}dterf(x)=π1∫−xxe−t2dt=π2∫0xe−t2dt
累积分布函数图形如下: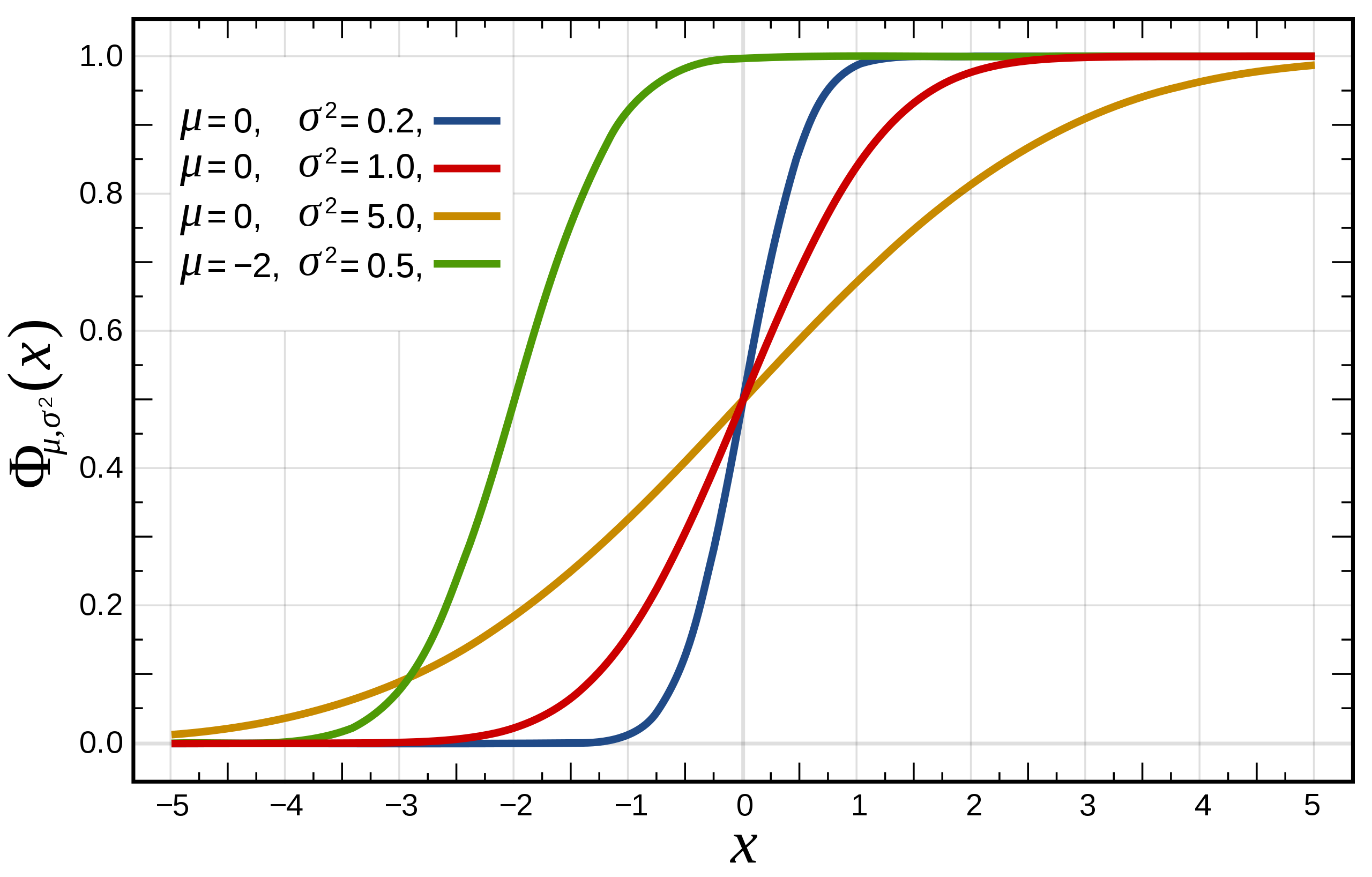
7.1.4 Φ(x)与erf(x)函数关系公式推导
Φ ( x ) = 1 2 π ∑ − ∞ x e − t 2 2 d t = 2 2 π ∑ − ∞ x e − ( t 2 ) 2 d t 2 Φ(x)=\frac{1}{\sqrt{2\pi}}\sum_{-\infty}^xe^{-\frac{t^2}{2}}dt=\frac{\sqrt{2}}{\sqrt{2\pi}}\sum_{-\infty}^{x}e^{-(\frac{t}{\sqrt{2}})^2}d\frac{t}{\sqrt{2}}Φ(x)=2π1∑−∞xe−2t2dt=2π2∑−∞xe−(2t)2d2t
= 1 π ∑ − ∞ x 2 e − z 2 d z = 1 π ∑ − ∞ 0 e − z 2 d z + 1 π ∑ 0 x 2 e − z 2 d z =\frac{1}{\pi}\sum_{-\infty}^{\frac{x}{\sqrt{2}}}e^{-z^2}dz=\frac{1}{\pi}\sum_{-\infty}^0e^{-z^2}dz+\frac{1}{\pi}\sum_{0}^{\frac{x}{\sqrt{2}}}e^{-z^2}dz=π1∑−∞2xe−z2dz=π1∑−∞0e−z2dz+π1∑02xe−z2dz
= 1 2 + 1 2 e r f ( x π ) = 1 2 [ 1 + e r f ( x 2 ) ] =\frac{1}{2}+\frac{1}{2}erf(\frac{x}{\sqrt{\pi}})=\frac{1}{2}\begin{bmatrix}1+erf(\frac{x}{\sqrt{2}})\end{bmatrix}=21+21erf(πx)=21[1+erf(2x)]
8 GeLu激活函数
GAUSSIAN ERROR LINEAR UNITS (GELUS)
论文中对比了GeLu激活函数在试验效果比ReLu,ELU都好,加上在bert中的应用,最近引起了广泛的关注。
函数数学公式:
f ( x ) = x P ( X ≤ x ) = x Φ ( x ) f(x)= xP(X \le x) = xΦ(x)f(x)=xP(X≤x)=xΦ(x)
其中 Φ ( x ) = 1 2 [ 1 + e r f ( x 2 ) ] ( 1 ) Φ(x)=\frac{1}{2}\begin{bmatrix}1+erf(\frac{x}{\sqrt{2}}) \end{bmatrix} { (1)}Φ(x)=21[1+erf(2x)](1)
X ∼ N ( 0 , 1 ) , Φ ( x ) X∼N(0,1){,}Φ(x)X∼N(0,1),Φ(x)是标准正态分布的累积分布函数,论文提供的近似求解公式:
f ( x ) = x Φ ( x ) = 0.5 x ( 1 + t a n h [ 2 / π ( x + 0.044715 x 3 ) ] ) ( 2 ) f(x)=xΦ(x)=0.5x(1+tanh[ \sqrt{2/\pi}(x+0.044715x^3)]) {(2)}f(x)=xΦ(x)=0.5x(1+tanh[2/π(x+0.044715x3)])(2)
函数图形:
函数导数图形: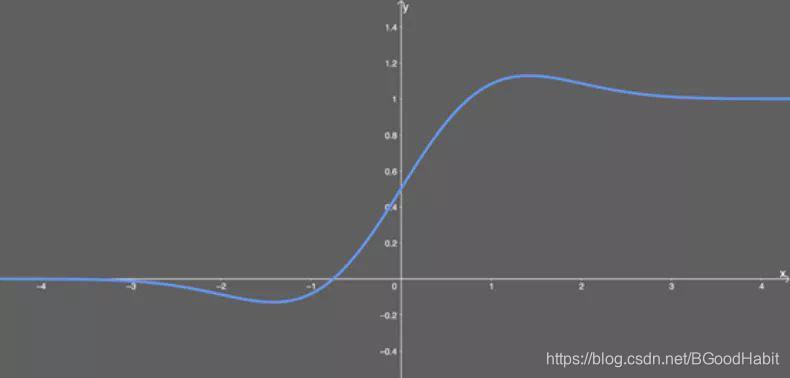
8.1 GeLu激活函数的直观理解
GeLu函数综合了dropout和ReLu的特色,从上面公式我们也可以看出,从ReLu, Leakly ReLu,ELU等,都是在对输入神经元乘以1或者0或者一个a aa常量进行变化,当x ≥ 0 x \ge 0x≥0的时候,以上三个函数都是乘以1作为神经元的输出,当x ≤ 0 x \le 0x≤0的时候,则乘以0或者a aa作为神经元的输出。
但GeLu是对x xx乘以标准正态分布的累积分布函数,根据x xx的输入,平滑的进行变化,随着x变小,Φ ( x ) Φ(x)Φ(x)变小,则神经元的输入x xx会以大概率的情况下“丢弃",整个过程相对ReLu激活函数更smooth
8.2 GeLu函数的公式推导
误差函数与标准正态分布的积分累积分布函数的关系为:Φ ( x ) = 1 2 [ 1 + e r f ( x 2 ) ] Φ(x)=\frac{1}{2}\begin{bmatrix}1+erf(\frac{x}{\sqrt{2}}) \end{bmatrix}Φ(x)=21[1+erf(2x)]
从上述(1)和(2)公式可以看出,需要证明:
e r f ( x 2 ) ≈ t a n h ( 2 π ( x + a x 3 ) ) erf(\frac{x}{\sqrt2}) \approx tanh(\sqrt{\frac{2}{\pi}}(x+ax^3))erf(2x)≈tanh(π2(x+ax3))其中a ≈ 0.044715 a \approx 0.044715a≈0.044715
证明如下:
泰勒级数
在数学上,对于一个实数或复数a aa领域上,以实数作为变量或以复数作为变量的函数,并且是无穷可微的函数f ( x ) f(x)f(x),它的泰勒级数是以下这种形式的幂级数:
f ( x ) = ∑ n = 0 ∞ f ( n ) ( a ) n ! ( x − a ) n f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^nf(x)=n=0∑∞n!f(n)(a)(x−a)n这里n ! n!n!表示n nn的阶乘,而f ( n ) ( a ) f^{(n)}(a)f(n)(a)表示函数f ff在点a aa处的n nn阶导数,如果a = 0 a=0a=0,也可以把这个级数称为麦克劳林级数。
指数函数e x e^xex的等价幂级数:
e x = 1 + ∑ n = 1 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + . . . e^x=1+\sum_{n=1}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+...ex=1+n=1∑∞n!xn=1+x+2!x2+3!x3+4!x4+...
t a n h ( x ) tanh(x)tanh(x)的泰勒级数:t a n h ( x ) = x − x 3 3 + o ( x 3 ) tanh(x)=x-\frac{x^3}{3}+o(x^3)tanh(x)=x−3x3+o(x3)
e r f ( x ) erf(x)erf(x)的泰勒级数:e r f ( x ) = 2 π ( x − x 3 3 ) + o ( x 3 ) erf(x)=\frac{2}{\sqrt{\pi}}(x-\frac{x^3}{3})+o(x^3)erf(x)=π2(x−3x3)+o(x3)
t a n h ( 2 π ( x + a x 3 ) ) = 2 π ( x + ( a − 2 3 π ) x 3 ) + o ( x 3 ) (3) tanh(\sqrt{\frac{2}{\pi}}(x+ax^3)) = \sqrt{\frac{2}{\pi}}(x+(a-\frac{2}{3\pi})x^3)+o(x^3) \text{ }\text{ }\text{(3) }tanh(π2(x+ax3))=π2(x+(a−3π2)x3)+o(x3) (3)
e r f ( x 2 ) = 2 π ( x − x 3 6 ) + o ( x 3 ) (4) erf(\frac{x}{\sqrt{2}})=\sqrt{\frac{2}{\pi}}(x-\frac{x^3}{6})+o(x^3) \text{ }\text{ }\text{(4) }erf(2x)=π2(x−6x3)+o(x3) (4)
令公式(3)和公式(4)相等,则a ≈ 0.04553992412 a \approx 0.04553992412a≈0.04553992412,与论文中a aa为0.044715十分接近。
bert中的glue函数实现如下:
def gelu(x):
cdf = 0.5 * (1.0 + tf.tanh(
(np.sqrt(2 / np.pi) * (x + 0.044715 * tf.pow(x,3))))
return x * cdf
说明:本文图片素材来源Casper Hansen博文以及wikipedia