文章目录
6.1
待完善
6.2
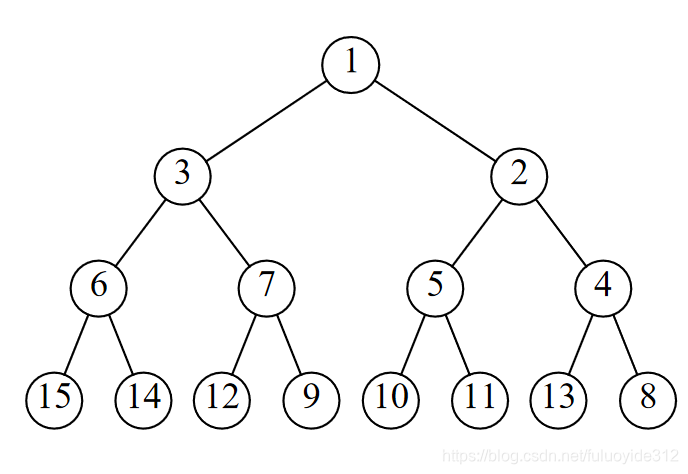
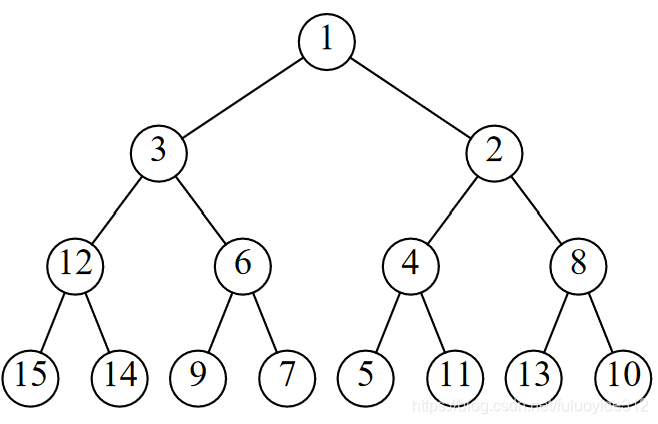
static void PercolateDown(int index,ElementType Data[],int Length)
{
ElementType Temp;
int i,Child;
for(i=index;i*2<=Length;i=Child)
{
Child=i*2;
if(Child!=Length&&Data[Child]>Data[Child+1])
Child++;
if(Data[i]>Data[Child])
{
Temp=Data[i];
Data[i]=Data[Child];
Data[Child]=Temp;
}
else
break;
}
}
void BuildHeap(ElementType Data[],int Length,PriorityQueue H)
{
if(!IsEmpty(H))
{
Error("Make PriorityQueue be initialized!");
return;
}
for(int index=1;index<=Length;index++)
H->Elements[index]=Data[index-1];
H->Size=Length;
for(int index=Length/2;index>0;index--)
PercolateDown(index,H->Elements,Length);
}
6.3
- 继承6.2a
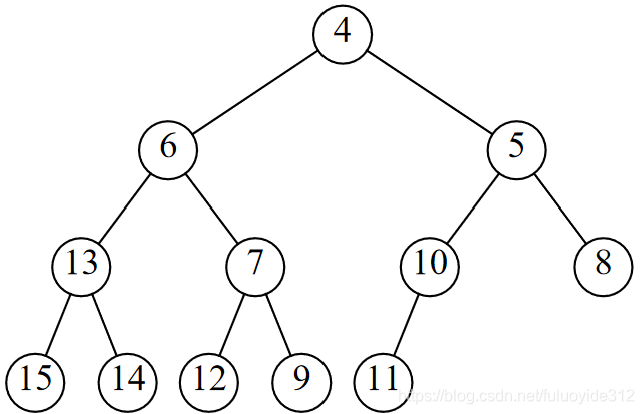
- 继承6.2b
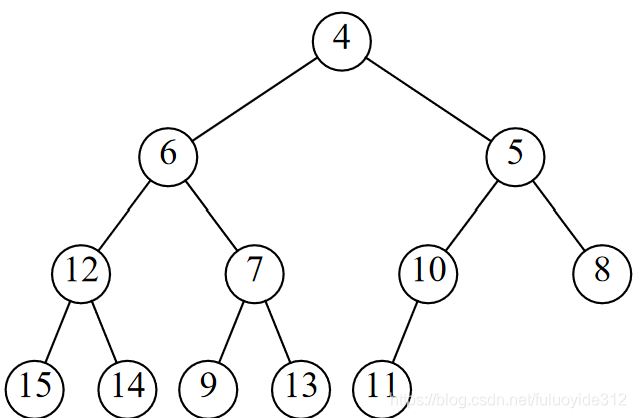
6.4
void PercolateUp(int index,ElementType Data[],int Length)//假设在数组下标为零的位置设置了值为INT_MIN的sentinel
{
int i,parent;
ElementType Temp;
for(i=index;i>0;i=parent)
{
parent=i/2;
if(Data[i]<Data[parent])
{
Temp=Data[i];
Data[i]=Data[parent];
Data[parent]=Temp;
}
}
}
static void PercolateDown(int index,ElementType Data[],int Length)
{
ElementType Temp;
int i,Child;
for(i=index;i*2<=Length;i=Child)
{
Child=i*2;
if(Child!=Length&&Data[Child]>Data[Child+1])
Child++;
if(Data[i]>Data[Child])
{
Temp=Data[i];
Data[i]=Data[Child];
Data[Child]=Temp;
}
else
break;
}
}
6.5
BinaryHeap.H
#ifndef _BinaryHeap_H
#define _BinaryHeap_H
typedef int ElementType;
struct HeapStruct;
typedef struct HeapStruct *PriorityQueue;
PriorityQueue Initialize(int MaxElements);
void Destroy(PriorityQueue H);
void MakeEmpty(PriorityQueue H);
void Insert(ElementType X,PriorityQueue H);
ElementType DeleteMin(PriorityQueue H);
ElementType FindMin(PriorityQueue H);
int IsEmpty(PriorityQueue H);
int IsFull(PriorityQueue H);
void BuildHeap(ElementType Data[],int Length,PriorityQueue H);
void DecreaseKey(int index,int delta,PriorityQueue H);
void IncreaseKey(int index,int delta,PriorityQueue H);
void Delete(int index,PriorityQueue H);
#endif
BinaryHeap.c
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>
#include "BinaryHeap.h"
#define MinPQSize 1
struct HeapStruct
{
int Capacity;
int Size;
ElementType *Elements;
};
static void FatalError(char *string);
static void Error(char *string);
static void PercolateUp(int index,ElementType Data[],int Length);
static void PercolateDown(int index,ElementType Data[],int Length);
static void FatalError(char *string)
{
fputs(string,stderr);
putc('\n',stderr);
exit(EXIT_FAILURE);
}
static void Error(char *string)
{
fputs(string,stderr);
putc('\n',stderr);
}
static void PercolateUp(int index,ElementType Data[],int Length)//假设在数组下标为零的位置设置了值为INT_MIN的sentinel
{
int i,parent;
ElementType Temp;
for(i=index;i>0;i=parent)
{
parent=i/2;
if(Data[i]<Data[parent])
{
Temp=Data[i];
Data[i]=Data[parent];
Data[parent]=Temp;
}
}
}
static void PercolateDown(int index,ElementType Data[],int Length)
{
ElementType Temp;
int i,Child;
for(i=index;i*2<=Length;i=Child)
{
Child=i*2;
if(Child!=Length&&Data[Child]>Data[Child+1])
Child++;
if(Data[i]>Data[Child])
{
Temp=Data[i];
Data[i]=Data[Child];
Data[Child]=Temp;
}
else
break;
}
}
PriorityQueue Initialize(int MaxElements)
{
PriorityQueue H;
if(MaxElements<MinPQSize)
Error("Priority queue is too small!");
H=malloc(sizeof(struct HeapStruct));
if(H==NULL)
FatalError("Out of space to create Priority queue!");
H->Elements=malloc(sizeof(ElementType)*(MaxElements+1));
if(H->Elements==NULL)
FatalError("Out of space for elements!");
H->Capacity=MaxElements;
H->Size=0;
H->Elements[0]=INT_MIN;
return H;
}
void BuildHeap(ElementType Data[],int Length,PriorityQueue H)
{
if(!IsEmpty(H))
{
Error("Make PriorityQueue be initialized!");
return;
}
for(int index=1;index<=Length;index++)
H->Elements[index]=Data[index-1];
H->Size=Length;
for(int index=Length/2;index>0;index--)
PercolateDown(index,H->Elements,Length);
}
void Destroy(PriorityQueue H)
{
if(H==NULL)
Error("Priority queue isn't exist!");
else
{
free(H->Elements);
free(H);
}
}
void MakeEmpty(PriorityQueue H)
{
if(H==NULL)
Error("Initiate first!");
else
{
H->Size=0;
}
}
void Insert(ElementType X,PriorityQueue H)
{
int i;
if(IsFull(H))
{
Error("Priority queue is full!");
return;
}
for(i=++H->Size;X<H->Elements[i/2];i/=2)
H->Elements[i]=H->Elements[i/2];
H->Elements[i]=X;
}
ElementType DeleteMin(PriorityQueue H)
{
int i,child;
ElementType MinElement,LastElement;
if(IsEmpty(H))
{
Error("Priority queue is empty!");
return H->Elements[0];
}
MinElement=H->Elements[1];
LastElement=H->Elements[H->Size--];
for(i=1;i*2<=H->Size;i=child)
{
child=i*2;
if(child!=H->Size&&H->Elements[child]>H->Elements[child+1])
child++;
if(LastElement>H->Elements[child])
H->Elements[i]=H->Elements[child];
else
break;
}
H->Elements[i]=LastElement;
return MinElement;
}
ElementType FindMin(PriorityQueue H)
{
if(IsEmpty(H))
{
Error("Priority queue is empty!");
return INT_MIN;
}
return H->Elements[1];
}
int IsEmpty(PriorityQueue H)
{
return H->Size==0;
}
int IsFull(PriorityQueue H)
{
return H->Size==H->Capacity;
}
void DecreaseKey(int index,int delta,PriorityQueue H)
{
H->Elements[index]-=delta;
PercolateUp(index,H->Elements,H->Size);
}
void IncreaseKey(int index,int delta,PriorityQueue H)
{
H->Elements[index]+=delta;
PercolateDown(index,H->Elements,H->Size);
}
void Delete(int index,PriorityQueue H)
{
ElementType min=FindMin(H);
DecreaseKey(index,H->Elements[index]-min+1,H);
DeleteMin(H);
}
test.c
#include <stdio.h>
#include "BinaryHeap.h"
int main(void)
{
int arr[]={8,3,4,2,5};
PriorityQueue H=Initialize(13);
BuildHeap(arr,5,H);
Insert(11,H);
printf("The minimum is %d\n",FindMin(H));
IncreaseKey(1,8,H);
printf("The minimum is %d\n",FindMin(H));
DecreaseKey(4,7,H);
printf("The minimum is %d\n",FindMin(H));
Delete(2,H);
while(!IsEmpty(H))
printf("Now,the minimum is %d\n",DeleteMin(H));
Destroy(H);
return 0;
}
6.6
一颗高度为h的完全平衡二叉树有2 h + 1 − 1 2^{h+1}-12h+1−1个节点,图中有15个节点在最深层没有儿子,所以再减去30个节点,一共225个。
6.7
待完善
6.8
待完善
6.9
- 对二叉堆使用先序遍历
ElementType PreOrder(PriorityQueue H)
{
if(Element小于X)
{
返回Element
PreOrder(H的左儿子)
PreOrder(H的右儿子)
}
}
- 左势堆和斜堆可行,d-堆时间界将是O(kd),二项队列不可行。
6.10
待完善
6.11
详细代码
a.
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include "BinaryHeap.h"
int main(void)
{
srand((unsigned int)time(0));
fputs("指定一个整数M,随机生成M个元素作为输入:",stdout);
int M,index;
fscanf(stdin,"%d",&M);
// ElementType arr[M];这么写的话,M过大栈会溢出,分配到堆上好些
ElementType *arr;
arr=malloc(sizeof(ElementType)*M);
for(index=0;index<M;index++)
arr[index]=rand()%10000+1;
PriorityQueue H=Initialize(2*M);
clock_t start,end;
start=clock();
for(index=0;index<M;index++)
Insert(arr[index],H);
end=clock();
printf("时间%ld",(end-start));//毫秒
Destroy(H);
return 0;
}
b.
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include "BinaryHeap.h"
int main(void)
{
srand((unsigned int)time(0));
fputs("指定一个整数M,随机生成M个元素作为输入:",stdout);
int M,index;
fscanf(stdin,"%d",&M);
ElementType *arr;
arr=malloc(sizeof(ElementType)*M);
for(index=0;index<M;index++)
arr[index]=rand()%10000+1;
PriorityQueue H=Initialize(2*M);
clock_t start,end;
start=clock();
BuildHeap(arr,M,H);
end=clock();
printf("时间%ld",(end-start));
Destroy(H);
return 0;
}
6.12
待完善
6.13
父亲位于( i + d − 2 ) d \frac {(i+d-2)} dd(i+d−2),儿子位于( i − 1 ) ∗ d + 2 (i-1)*d+2(i−1)∗d+2至i d + 1 id+1id+1。
6.14
- O ( ( M + d N ) l o g d N ) O((M+dN)log_dN)O((M+dN)logdN)
- O ( ( M + N ) l o g N ) O((M+N)logN)O((M+N)logN)
- O ( M + N 2 ) O(M+N^2)O(M+N2)
- d = m a x ( 2 , M N ) d=max(2,{\frac M N})d=max(2,NM)
6.15
待完善
6.16
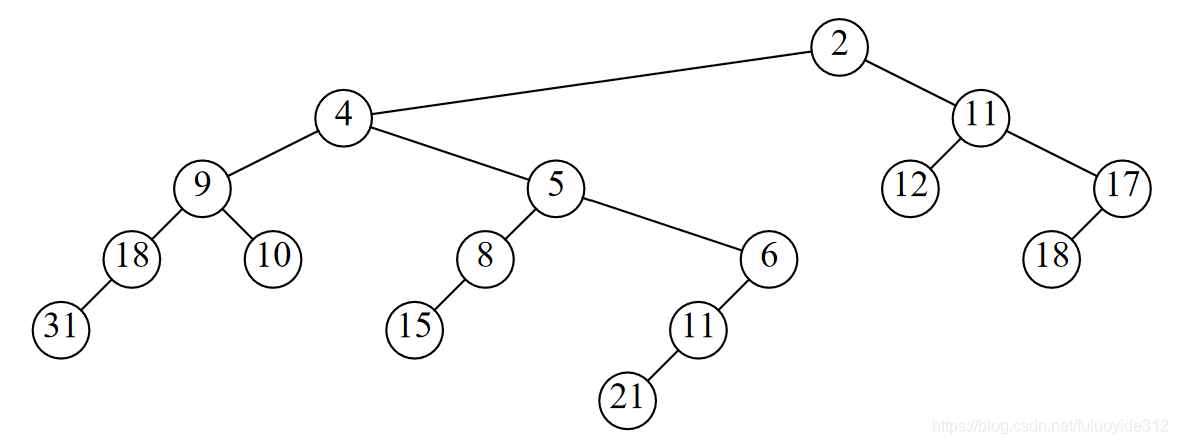
6.17
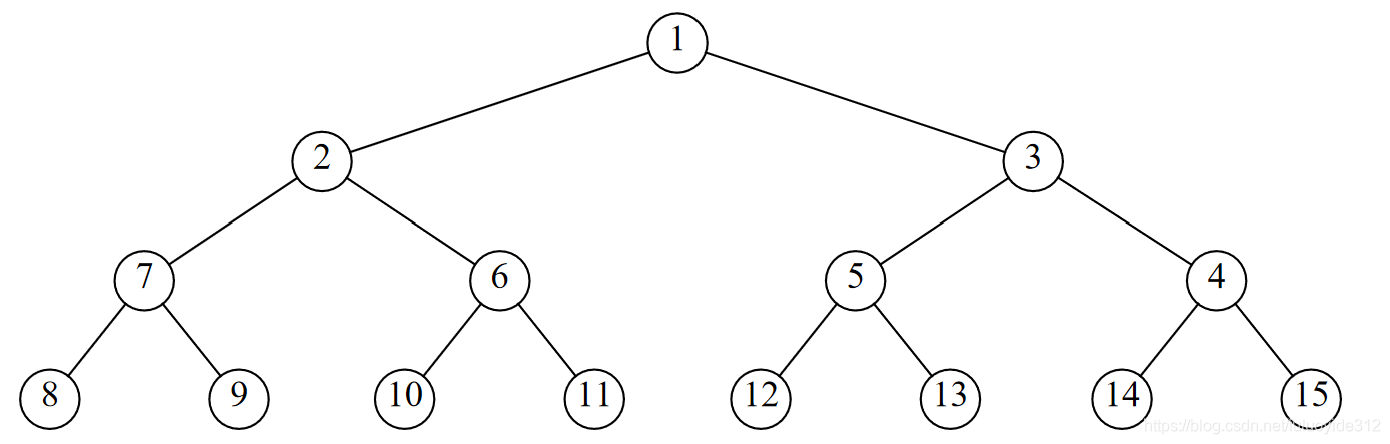
6.18
根据上一题的答案,当1 ≤ k ≤ 15 1 \leq k\leq 151≤k≤15时都是成立的,假设k = n k=nk=n时推论也成立,这时候将1,2,3……2 n − 1 2^n-12n−1依次插入树中,恰好第i层有2 i 2^i2i个节点(根节点在第0层,i=0,1,2……n-1)。这时候当k = ( n + 1 ) k=(n+1)k=(n+1)时,插入的关键字序列是1,2,3……2 n − 1 2^n-12n−1,2 n 2^n2n……2 n + 1 − 1 2^{n+1}-12n+1−1。新增的节点数为( 2 n + 1 − 1 ) − ( 2 n − 1 ) = 2 n (2^{n+1}-1)-(2^n-1)=2^n(2n+1−1)−(2n−1)=2n,正好填满第n层,满足完全平衡的要求,所以推论成立。
6.19
当输入关键字为逆序输入时,这时候左式堆将形成一个只有一连串左儿子的长链,这时候的右路径最短。
6.20
在很深的节点执行PercolateUp的操作将会非常昂贵,更有效的做法是对x为根的子树执行delete,然后再对其左右子树执行merge以形成新的子树代替原来的子树(之后原x的父节点到根节点都需要重新调整结构特性,最多有l o g N logNlogN个节点会受到影响),而对于想要进行DecreaseKey的x节点则可以执行Insert操作。
6.21
待完善
6.22
分步完成,当首元素重新出现在一个出队操作的堆中时,意味着下一步开始。第一次合并,将有N / 2 N/2N/2次merge发生在右路径不超过1个节点的heap间,而且因为合并的时间与右路径的长的和成正比,所以将有2 ∗ 1 ∗ ( N / 2 ) 2*1*(N/2)2∗1∗(N/2)个时间单位。第二次合并,将有N / 4 N/4N/4次merge发生在右路径不超过2个节点的heap间,所以将有2 ∗ 2 ∗ ( N / 4 ) 2*2*(N/4)2∗2∗(N/4)个时间单位,以此类推,2 ∗ 3 ∗ ( N / 4 ) 2*3*(N/4)2∗3∗(N/4)……
和为4N,于是O ( N ) O(N)O(N).
该算法的右路径更短。
6.23
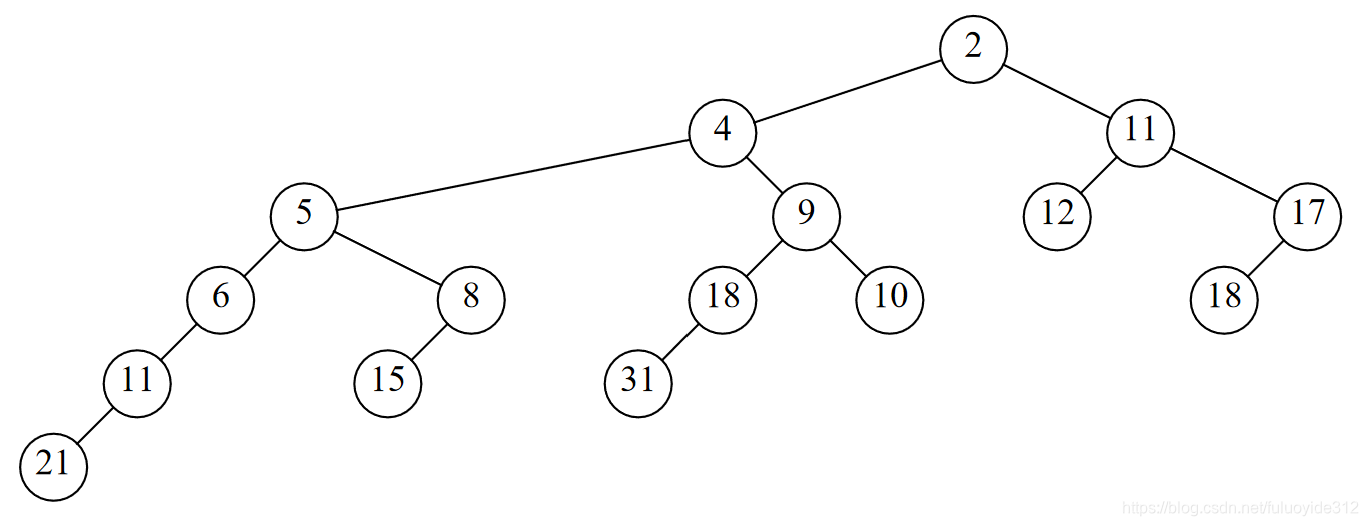
6.24
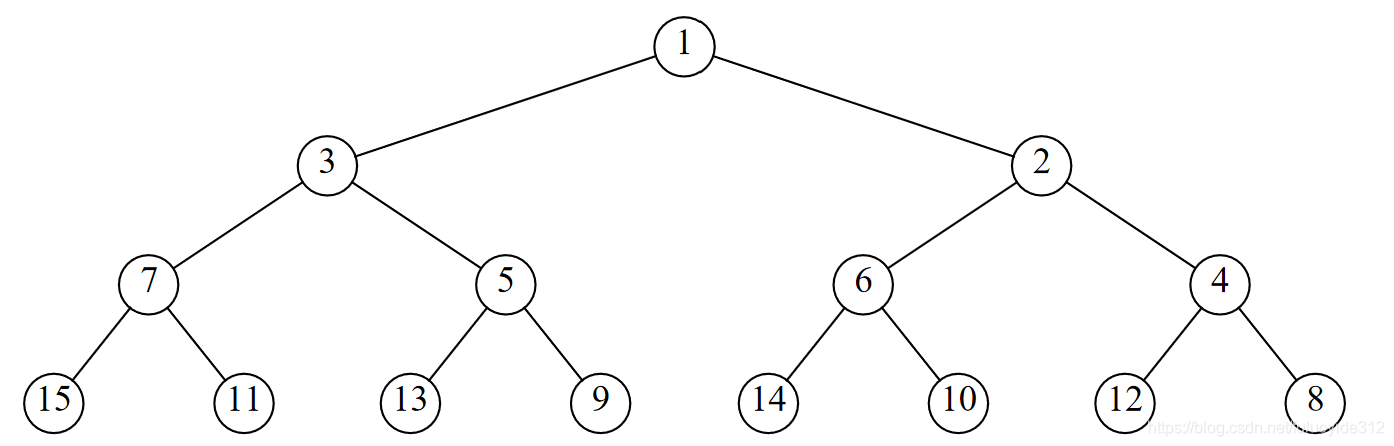
6.25
推论成立,证明方法同6.18。
6.26
可以,时间界依旧是O ( N ) O(N)O(N)
6.27
推论成立。显然当k=1时成立,假设i=1,2,……k时都成立。这时候B k + 1 B_{k+1}Bk+1由一个B k B_kBk附加到另一个B k B_kBk的根上形成,由假设得到其中一个B k B_kBk包含二项树B 0 B_0B0,B 1 B_1B1……B k − 1 B_{k-1}Bk−1,再加上另一个B k B_kBk,得到B k + 1 B_{k+1}Bk+1含有二项树B 0 B_0B0,B 1 B_1B1……B k − 1 B_{k-1}Bk−1,B k B_kBk。故推论成立。
6.28
归纳法,当k=1时,显然成立。假设i=1,2,3……k时都成立。这时B k + 1 B_{k+1}Bk+1是由一个B k B_kBk附加到另一个B k B_kBk的根上形成的。那么初始的B k B_kBk在深度d的有( d k ) (^k_d)(dk)个节点,附加的B k B_kBk在深度d-1处(也就是新形成的树的深度d处)有( d − 1 k ) (^k_{d-1})(d−1k)个节点。相加得知推论成立。
6.29
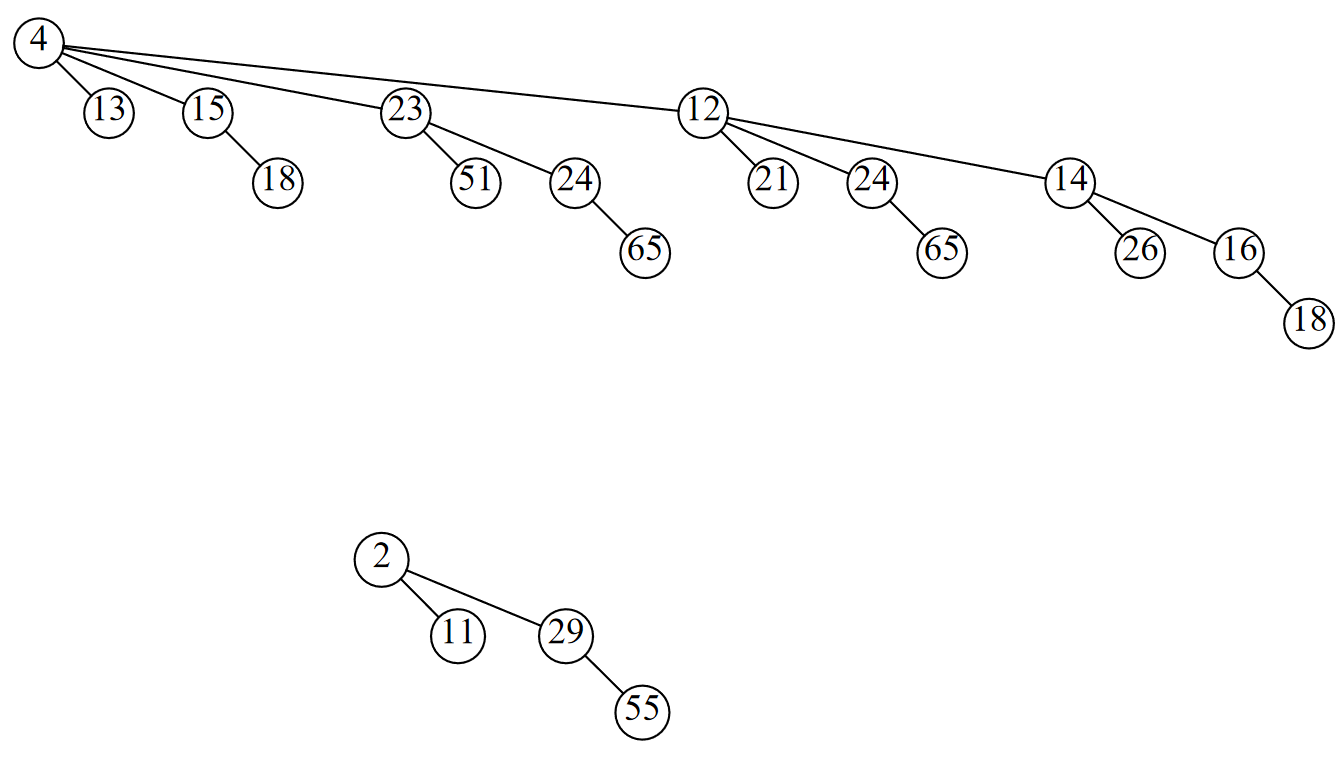
6.30
待完善
6.31
BinQueue Insert(ElementType X,BinQueue H)
{
BinTree Temp;
Temp=MakeSingleNodeTree(X);
H->CurrentSize+=1;
for(int index=0,j=1;j<=H->CurrentSize;index++,j=j<<1)
{
if(H->TheTrees[index]==NULL)
{
H->TheTrees[index]=Temp;
break;
}
else
{
Temp=CombineTrees(Temp,H->TheTrees[index]);
H->TheTrees[index]=NULL;
}
}
return H;
}
6.32
BinQueue Merge(BinQueue H1,BinQueue H2)
{
if(H1==H2)
{
Error("Can't merge the same Binomial queue!");
return H1;
}
else
{
if(H1->CurrentSize<H2->CurrentSize)
{
BinQueue Temp;
Temp=H1;
H1=H2;
H2=Temp;
}
BinTree T1,T2,Carry=NULL;
int i,j;
if(H1->CurrentSize+H2->CurrentSize>Capacity)
{
Error("Merge would exceed capacity!");
}
H1->CurrentSize+=H2->CurrentSize;
for(i=0,j=1;j<=H1->CurrentSize;i++,j=j<<1)
{
T1=H1->TheTrees[i];
T2=H2->TheTrees[i];
switch(!!T1+2*!!T2+4*!!Carry)
{
case 0:/*这个高度上没有树*/
case 1:/*这个高度上只有H1的树存在,保持不变*/
break;
case 2:/*这个高度上只有H2的树存在,交换到H1*/
H1->TheTrees[i]=T2;
H2->TheTrees[i]=NULL;
break;
case 3:/*这个高度上H1和H2的树都存在*/
Carry=CombineTrees(T1,T2);
H1->TheTrees[i]=H2->TheTrees[i]=NULL;
break;
case 4:/*这个高度只有Carry存在,放到H1*/
H1->TheTrees[i]=Carry;
Carry=NULL;
break;
case 5:/*这个高度H1的树和Carry存在*/
Carry=CombineTrees(Carry,T1);
H1->TheTrees[i]=NULL;
break;
case 6:/*这个高度H2的树和Carry存在*/
Carry=CombineTrees(Carry,T2);
H2->TheTrees[i]=NULL;
break;
case 7:/*这个高度上三个都存在,将Carry放到H1*/
H1->TheTrees[i]=Carry;
Carry=CombineTrees(T1,T2);
H2->TheTrees[i]=NULL;
break;
}
if(j>H2->CurrentSize&&(!!T2+!!Carry==0))
return H1;
}
return H1;
}
}
ElementType DeleteMin(BinQueue *H)//因为修改了Merge使得较小的二项队列总是被合并的较大的队列中,所以返回的二项队列会改变,因为懒得修改DeleteMin,所以就把参数简单变成二项队列的指针算了
{
ElementType MinItem=INT_MAX;
int MinTree;
int i,j;
BinQueue DeletedQueue;
Position DeletedTree,OldRoot;
if(IsEmpty(*H))
{
Error("Empty binomial queue!");
return INT_MIN;
}
for(i=0;i<MaxTrees;i++)
{
if((*H)->TheTrees[i]&&(*H)->TheTrees[i]->Element<MinItem)
{
MinItem=(*H)->TheTrees[i]->Element;
MinTree=i;
}
}
OldRoot=DeletedTree=(*H)->TheTrees[MinTree];
DeletedTree=DeletedTree->LeftChild;
free(OldRoot);
DeletedQueue=Initialize();
DeletedQueue->CurrentSize=(1<<MinTree)-1;
for(j=MinTree-1;j>=0;j--)
{
DeletedQueue->TheTrees[j]=DeletedTree;
DeletedTree=DeletedTree->NextSibling;
DeletedQueue->TheTrees[j]->NextSibling=NULL;
}
(*H)->TheTrees[MinTree]=NULL;
(*H)->CurrentSize-=DeletedQueue->CurrentSize+1;
(*H)=Merge(*H,DeletedQueue);
return MinItem;
}
6.33
待完善
6.34
待完善
6.35
额外保存一个值作为基准值,而在节点中只保存该节点和其父节点的值的差,这样一来,只需要修改基准值就可以实现O ( 1 ) O(1)O(1)时间界的DecreaseAllKeys。
6.36
待完善