一、k-means算法概述
k-means算法和KNN算法虽然都是以近邻信息来标注类别,但却是两类不同的算法:KNN算法是监督学习中的基本分类与回归算法,而k-means算法是无监督学习中的聚类算法。
聚类是指将未标注的样本数据中相似的分为同一类,即“物以类聚,人以群分”。k-means算法是聚类算法中最为简单、高效的核心思想:指定k个初始质心(initial centroids),作为聚类的类别(cluster),重复迭代直至算法收敛。k-means算法的流程可表示如下:
选取k个初始质心(作为初始cluster);
repeat:
对每个样本点,计算得到距其最近的质心,将其类别标记为该质心所对应的cluster;
重新计算k个cluster对应的质心;
until 质心不再发生变化
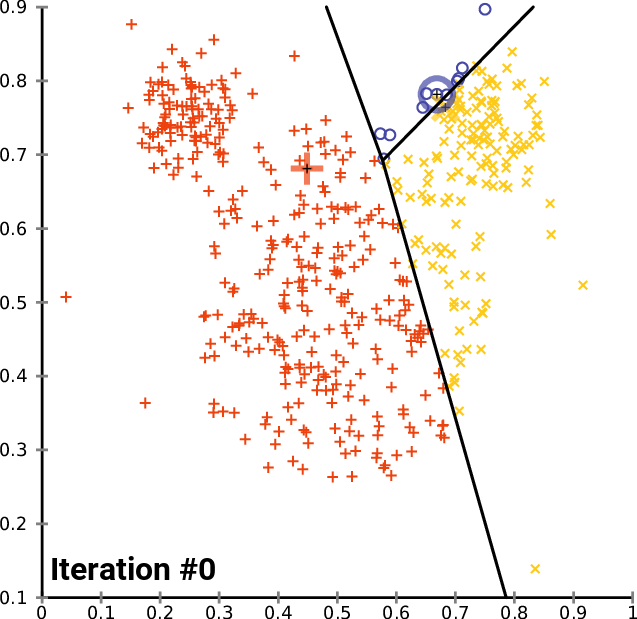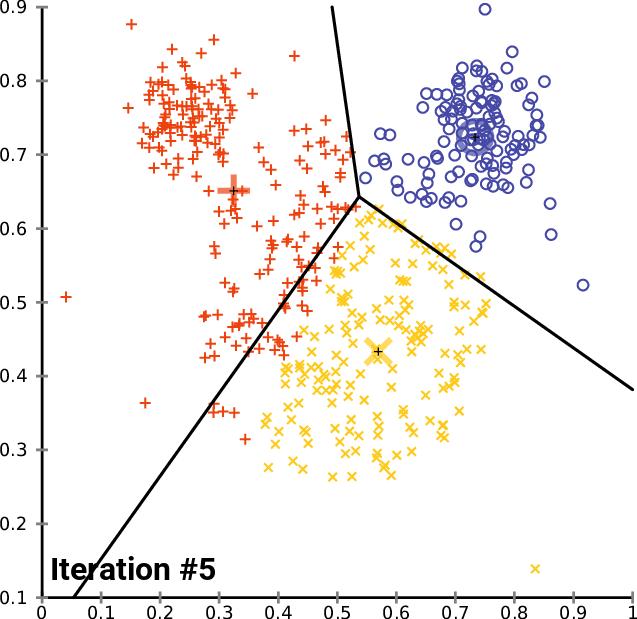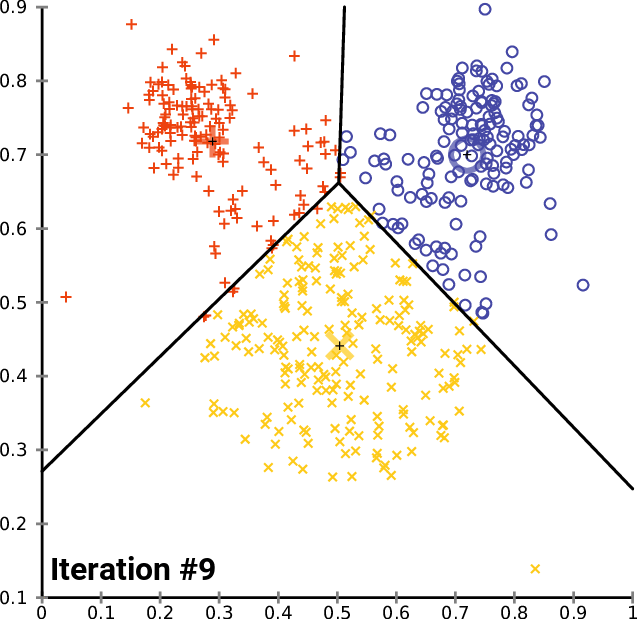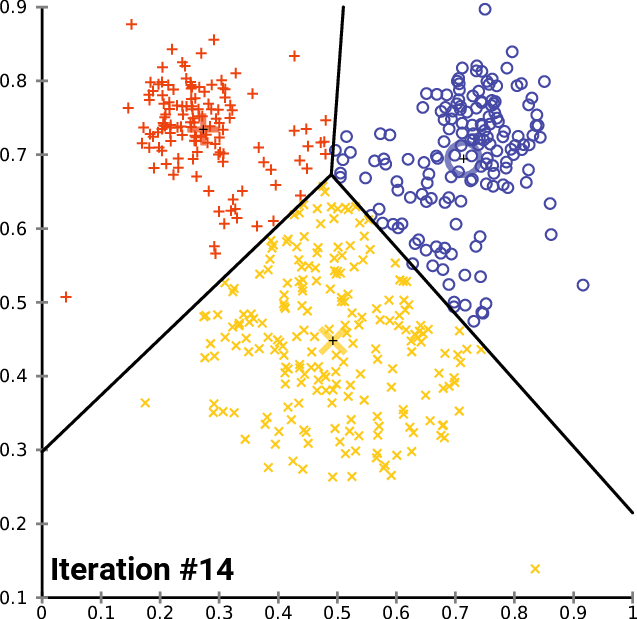
为了衡量k-means算法不同聚类结果的好坏,以平方误差和(sum of squared error,SSE)作为聚类的目标函数:
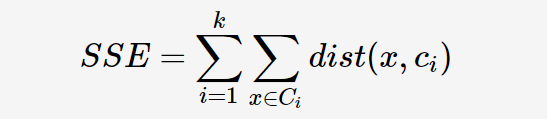
其中,dist表示样本点x到cluster Ci的质心ci的距离平方和。
k-means算法最优的聚类结果应使SSE达到最小值。
ps:
①由于SSE是一个非凸函数(non-convex function),所以SSE不能保证找到全局最优解,只能确保局部最优解。但是可以重复执行几次k-means算法,选取SSE最小的一次作为最终的聚类结果;
②SSE是一个严格的坐标下降(Coordinate Decendet)过程。设目标函数SSE如下:
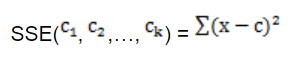
采用欧式距离作为变量之间的聚类函数。每次朝一个变量ci的方向找到最优解,也就是求偏导数,然后令其等于0,可得
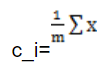
其中m是c_i所在的簇的元素的个数
也就是当前聚类的均值就是当前方向的最优解(最小值),这与kmeans的每一次迭代过程一样。所以,这样保证SSE每一次迭代时,都会减小,最终使SSE收敛。
二、k-means算法的缺点及优化方法
1、随机初始化
k-means算法开始执行时,通常随机选取k个初始质心作为初始cluster,这就使得k-means算法最后得出的结果会依赖于初始化的情况,并且可能因为初始化不恰当而造成次优的聚类结果(SSE较大):

为了解决这个问题,在基本k-means的基础上发展了二分(bisecting)k-means算法,其算法流程为:
初始只有一个cluster包含所有样本点;
repeat:
从待分裂的clusters中选择一个进行二元分裂,所选的cluster应使得SSE最小;
until 有k个cluster
二分k-means算法依次对每个待分裂的cluster进行二元分裂(bisect)以求得最优分裂。由于二分k-means算法初始化时只选择一个质心,故对初始质心的选择不太敏感,解决了基本k-means算法随机初始化带来的问题。
2、选择聚类数k
k值的选取也会直接影响聚类结果,最优聚类的k值应与样本数据本身的结果信息相吻合,而这种结果难以把握,因此要选取最优的k值时非常困难的。
为了解决这个问题,可以使用“肘部法则(Elbow method)”,即不断改变k值(from 1 to x),执行k-means算法,然后画出代价函数与k值的变化曲线,选择“肘点处”(即拐点处,这时代价函数和k值均较小)的值作为k的取值。
