深度学习训练之卷积核参数初始化（Constant、Random、Xavier、Kaiming）系统详细总结

1、卷积核Constant参数初始化

就是对前向计算卷积核的参数初始化，Constant就是一个简单的初始化，就是把卷积核的参数设置为常数，API（pytorch）如下：

torch.nn.init.constant_(tensor, val)  # val：自己设置的常数
torch.nn.init.ones_(tensor)  # 设置为1
torch.nn.init.zeros_(tensor)  # 设置为0

2、卷积核参数随机（random）初始化

2.1 随机分布的参数初始化

概率密度函数为

f

(

x

)

f(x)

f(x), 平均值为

E

(

x

)

E(x)

E(x)，方差为

V

a

r

(

x

)

Var(x)

Var(x)

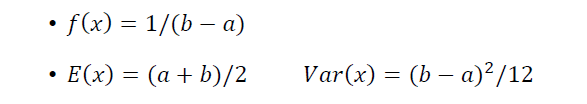
下面简单推导一下

E

(

x

)

E(x)

E(x)，

∫

a

b

x
 

d

x

\int_a^b {x} \,{\rm d}x

∫ab​xdx

=

x

2

2

∣

a

b

=\frac{x^2}{2}|_a^b

=2x2​∣ab​

=

b

2

−

a

2

2

=\frac{b^2-a^2}{2}

=2b2−a2​
平均值

E

(

x

)

=

b

2

−

a

2

2

⋅

(

b

−

a

)

=

(

a

+

b

)

/

2

E(x)=\frac{b^2-a^2}{2 \cdot(b-a)}=(a+b)/2

E(x)=2⋅(b−a)b2−a2​=(a+b)/2
API（pytorch）：

torch.nn.init.uniform_(tensor, a=0.0, b=1.0)

2.2 正态分布的参数初始化

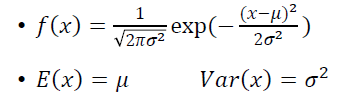
API（pytorch）：

torch.nn.init.normal_(tensor, mean=0.0, std=1.0)

3、卷积核参数Xavier初始化

一句话解释什么是Xavier初始化：输入和输出的feature map的标准差保持一致。
问题来了，为什么要输入和输出的feature map的标准差保持一致？
因为：输入和输出的feature map的标准差保持一致，可以防止过拟合。

下面开始推导Xavier分布的标准差：
假设输入

X

j

X_j

Xj​，权重为

W

i

,

j

W_{i,j}

Wi,j​，偏差为

B

i

B_i

Bi​，所以，输出为：

Y

i

=

∑

j

n

I

W

i

,

j

X

j

+

B

i

Y_i=\sum_{j}^{n_I}{W_{i,j}X_j+B_i}

Yi​=j∑nI​​Wi,j​Xj​+Bi​
其中

n

I

n_I

nI​为卷积核输入维度，比如卷积核为

3

×

3

3×3

3×3，输入channel为

3

3

3，则

n

I

=

3

×

3

×

3

n_I=3×3×3

nI​=3×3×3，

保证输入和输出的标准差一致，所以，

V

a

r

(

Y

i

)

=

V

a

r

(

∑

j

n

I

W

i

,

j

X

j

)

+

V

a

r

(

B

i

)

Var(Y_i)=Var(\sum_{j}^{n_I}{W_{i,j}X_j})+Var(B_i)

Var(Yi​)=Var(∑jnI​​Wi,j​Xj​)+Var(Bi​)
再设定

V

a

r

(

B

i

)

=

0

Var(B_i)=0

Var(Bi​)=0，
则：

V

a

r

(

Y

i

)

=

∑

j

n

I

V

a

r

(

W

i

,

j

)

V

a

r

(

X

j

)

=

n

I

V

a

r

(

W

i

,

j

)

V

a

r

(

X

j

)

Var(Y_i)=\sum_{j}^{n_I}Var(W_{i,j})Var(X_j)=n_IVar(W_{i,j})Var(X_j)

Var(Yi​)=∑jnI​​Var(Wi,j​)Var(Xj​)=nI​Var(Wi,j​)Var(Xj​)
因为：

V

a

r

(

Y

i

)

=

V

a

r

(

X

j

)

Var(Y_i)=Var(X_j)

Var(Yi​)=Var(Xj​)
所以：

V

a

r

(

W

i

,

j

)

=

1

n

I

Var(W_{i,j})=\frac{1}{n_I}

Var(Wi,j​)=nI​1​
即：Xavier分布的标准差为

n

I

{n_I}

nI​

3.1 基于Xavier的随机参数初始化和正态分布参数初始化

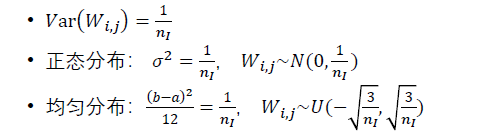
此推导不难，便不做赘述。

3.2 进阶版的Xavier

前面说的是前向传播，因为进行网络训练时，不能只有前向计算，也要有反向计算，而反向计算的初始化参数也应遵循保持方差一致，所以

V

a

r

(

W

i

,

j

)

=

i

n

O

Var(W_{i,j})=\frac{i}{n_O}

Var(Wi,j​)=nO​i​，取前向计算和反向计算的调和平均数，公式如下：

同理，反向传播的

V

a

r

(

W

i

,

j

)

=

1

n

O

Var(W_{i,j})=\frac{1}{n_O}

Var(Wi,j​)=nO​1​，

n

O

n_O

nO​为输出的维度，
再计算前向传播和反向传播的调和平均数为：

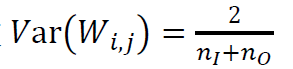
Xavier API（pytorch):

torch.nn.init.xavier_normal_(tensor, gain=1.0)

torch.nn.init.xavier_uniform_(tensor, gain=1.0)

4、卷积核参数Kaiming初始化

为什么提出Kaiming初始化？
答：因为在网络训练里有使用到relu激活函数，而relu的激活函数的负半轴为0，所以相应的方差为输入前feature map方差的一半，所以

V

a

r

(

W

i

,

j

)

=

2

n

I

Var(W_{i,j})=\frac{2}{n_I}

Var(Wi,j​)=nI​2​

具体推导如下：

Y

=

∑

r

e

l

u

(

Z

)

⋅

W

+

b

Y=\sum relu(Z)\cdot W+b

Y=∑relu(Z)⋅W+b
因为经过了

r

e

l

u

relu

relu，所以方差为输入前的一半，所以

V

a

r

(

y

)

=

2

V

a

r

(

r

e

l

u

(

Z

)

)

Var(y)=2Var(relu(Z))

Var(y)=2Var(relu(Z))
所以：

V

a

r

(

W

)

=

2

n

I

Var(W)=\frac{2}{n_I}

Var(W)=nI​2​

4.1 Kaiming初始化与均匀分布、正态分布

4.2 Kaiming初始化API（pytorch）

torch.nn.init.kaiming_normal_(tensor, a=0,mode='fan_in', nonlinearity='leaky_relu')

torch.nn.init.kaiming_uniform_(tensor, a=0,mode='fan_in', nonlinearity='leaky_relu')