TOPSIS方法建模实例-逾期催收等级建模

本文主要分为三部分：

第一部分，介绍原理和选择依据；

第二部分，介绍topsis的方法建模过程；

第三部分，建模总结。

通过这三部分的来描述如何建立C卡催收评分模型。

第一部分：我们先了解一下什么是Topsis方法。

TOPSIS法（Technique for Order Preferenceby Similarity to Ideal Solution,）逼近理想解排序法、理想点法；他是C.L.Hwang和K.Yoon于1981年首次提出，TOPSIS法根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。理想化目标（Ideal Solution）有两个，一个是肯定的理想目标（positive ideal solution）或称最优目标，一个是否定的理想目标（negative ideal solution）或称最劣目标，评价最好的对象应该是与最优目标的距离最近，而与最劣目标最远，距离的计算可采用明考斯基距离，常用的欧几里德几何距离是明考斯基距离的特殊情况。

TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。它通过归一化后的数据规范化矩阵,找出多个目标中最优目标和最劣目标(分别用理想解和反理想解表示) ,分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在0～1 之间,该值愈接近1,表示相应的评价目标越接近最优水平;反之,该值愈接近0,表示评价目标越接近最劣水平。该方法已经在土地利用规划、物料选择评估、项目投资、医疗卫生等众多领域得到成功的应用,明显提高了多目标决策分析的科学性、准确性和可操作性。

选择逾期有重要两个考虑因素：一个是逾期时间因素；一个是逾期金额因素；

往往逾期前期阶段容易收回，越往后，逾期期数越长，收回金额越大。（催收评分模型中因素选择可以重点考虑从用户的还款记录中提取，本文选择较为常见的数据作为变量，实际中笔者认为可以考虑10-16个因素为宜）。

另外需要说明一点，对于逾期和损失率的关系。

.

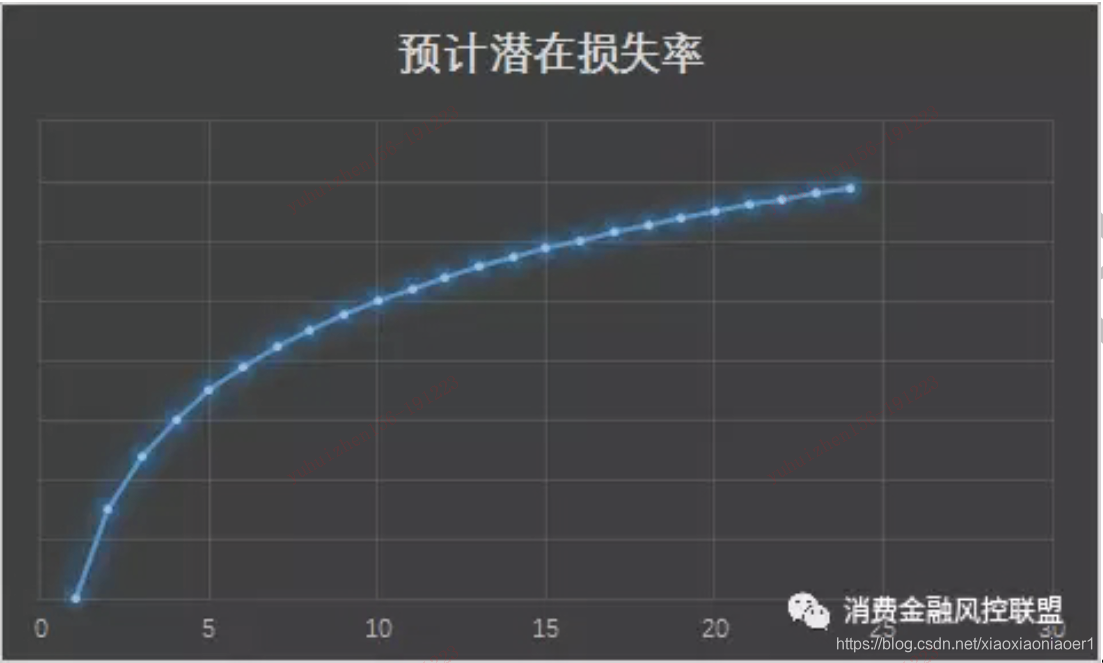
上图为理想化的潜在损失率示意图。预计潜在损失率，随着逾期期数增加，潜在损失率逐步提高。

数据准备阶段，建立同趋势化的数据；

第一步：进行评价指标同趋势化；

在进行建模时需要对各项指标（我们以合同金额、合同期限、逾期金额、逾期期数，逾期四个因素作为参考变量）要求方向一致，通常采用倒书法（原有的指标变成倒数即采用 x变成 1/x方法）。但是本文不采用倒数，采用对数和除数进行同趋势化处理。

数据如下（已经过脱敏处理）：

第二步:进行归一化处理

我们根据数学公式：

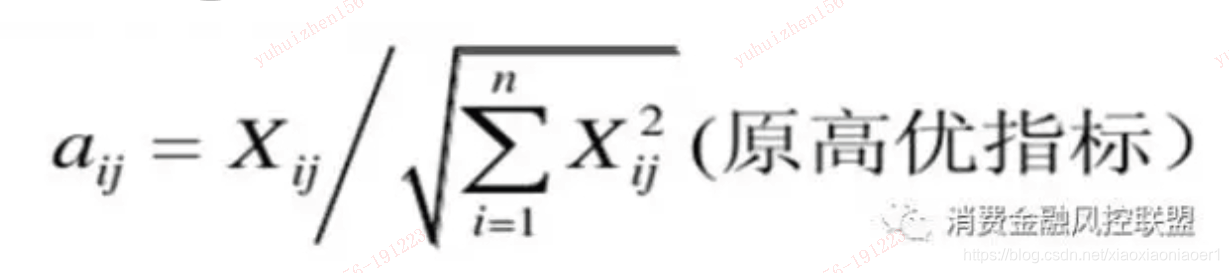
分别计算出逾期次数与逾期金额的归一化数据（也是我们重点使用的2个数据）

归一处理完成之后我再根据公式计算 D+， D-，值

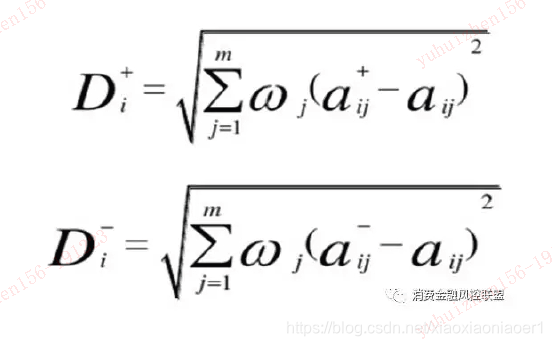
D数值其中需要考虑使用熵值法或者可以确定权重的方法，分布对I，J进行加权处理（加权也可以采用熵权法等其他方法处理），本次我们采用离散度指标作为逾期次数和逾期金额的权重换算，经过换算后  

有了权重值之后可以求出D+和D-

根据数值算出得分

我们目前根据D+D-值计算出C值，也就是我们通常说的得分

此次得分我们就用简单的算法，放大100倍取整数。

这次算是完成了一次使用topsis方法建模过程，也对29个数据项进行了评分，下一步也是重要的一步，根据前面提出来的四要素进行公式化。这一步过程我就不详细描述了，就是根据topsis公式确定的参数进行反推即可得到评分公式。

本次的分值的是（0，100），对于P等级划分来说，我们初步定义为P1-P5，5个等级可以根据p1（0，20)，P2(20,40)，P3(40,60)，P4(60,80)，P5(80,100)，也可以根据其他方式进行划分，例如采用对数方式划分，指数划分等方法，这里对于划分等级手段就不在赘述。

第三部分:总结一下

采用这种TOPSIS算法容易上手，入门比较容易，通过excle就可以完成整个建模过程。

建模之后还有很多需要做的工作，这里也不在赘述，具体的知识可以学习相关内容。

逾期催收评分卡在风控系统中的应用笔者总结了几个方面

1：可以让程序员或者建模师用C，C++，JAVA或者SPSS，SAS甚至PHP等工具来实现系统化，有输入输出，已经执行过程中的监控和迭代，在建模过程中也可以引入内外部变量，比如授信额度，授信评分等因素。

2：当有了评分、等级之后，评分作为输入项，可以根据风控决策系统分别走不同的路径，比如P1的可以走电催方式，分派给短信、人工点催，P2 P3可以走上门或者委外催收管理，P4可以启动资产保全或诉讼，P5可以走资产核销等流程，这一切都要根据实际情况和相关的风控政策来实行IT化落地。

3：任何建模仅仅只是根据历史遗忘数据做的一种数学匹配，建模完成仅仅是万里长征的第一步，后面要做的事情还有很多。对于消费金融模式，时间就是金钱就是市场的前提下，应该首先考虑简单模型的建设，用1-3中方式方法来快速建立模型，快速开发，但一定要谨慎使用模型的评价结果。在决策引擎中有一种模型叫做优胜者模式，可以使用决策模型在多个模型同时运行，以观察数据对模型的冲击和表现，再对模型进行迭代。

4：简单的东西不代表容易，复杂的东西也不一定好用，适合自己的场景和模式的模型才是最好的。银行模型只能作为参考，实际用在消费金融模式里还需要进一步验证和迭代。