内容来自ANDREA CORBELLINI的椭圆曲线密码学的介绍:Elliptic Curve Cryptography: a gentle introduction
文章目录
前言
本文是椭圆曲线介绍中的第二篇:整数域上面的椭圆曲线以及离散对数问题。
在上一篇中,一届看到了实数域上面的椭圆曲线以及如何用椭圆曲线的性质来定义一个群。两个点之间的加法定义为:一条直线与椭圆曲线的三个交点,他们的和为0:( P + Q + R = 0 ) (P+Q+R=0)(P+Q+R=0)。
标量乘法的定义为:( n P = P + P + ⋯ + P ) (nP=P+P+\cdots +P)(nP=P+P+⋯+P),可以使用类似二进制分解的方法加速标量乘法的运算。
现在将椭圆曲线限制到一个有限域中。
模p的整数域
有限域的概念可以参考这个链接。这里略过了。
F p 上 面 的 椭 圆 曲 线 \mathbb{F}_p上面的椭圆曲线Fp上面的椭圆曲线
在实数上面的椭圆曲线定义为:
{ ( x , y ) ∈ R 2 ∣ y 2 = x 3 + a x + b , 4 a 3 + 27 b 2 ≠ 0 } ∪ { 0 } \left\{(x,y)\in \mathbb{R}^2 \quad |\quad y^2 = x^3+ax+b,4a^3+27b^2\ne 0 \right\} \cup \{0\}{(x,y)∈R2∣y2=x3+ax+b,4a3+27b2=0}∪{0}
而有限域上面的椭圆曲线为:
{ ( x , y ) ∈ ( F p ) 2 ∣ y 2 = x 3 + a x + b ( m o d p ) , 4 a 3 + 27 b 2 ≠ 0 ( m o d p ) } ∪ { 0 } \left\{(x,y)\in (\mathbb{F}_p)^2 \quad |\quad y^2 = x^3+ax+b \pmod p,4a^3+27b^2\ne 0 \pmod p \right\} \cup \{0\}{(x,y)∈(Fp)2∣y2=x3+ax+b(modp),4a3+27b2=0(modp)}∪{0}
,其中0 00表示无穷远点,a aa和b bb是F p \mathbb{F}_pFp中的元素。
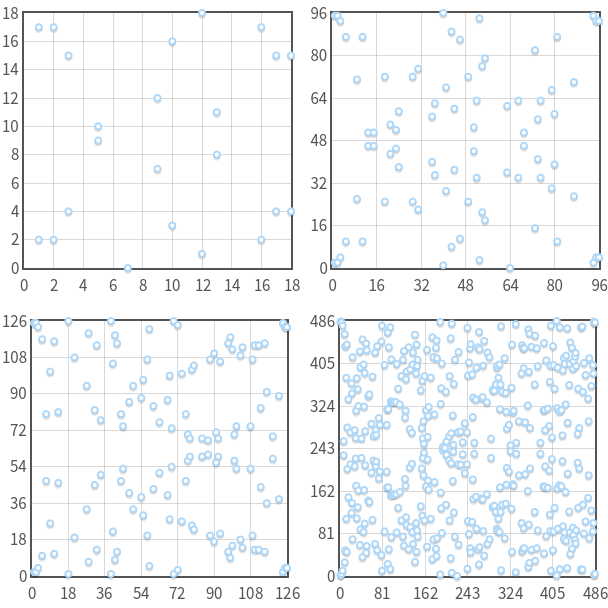
上面的图片分别为y 2 ≡ x 3 − 7 x + 10 ( m o d p ) y^2 \equiv x^3-7x+10 \pmod py2≡x3−7x+10(modp)在p = 19 , 97 , 127 , 487 p=19,97,127,487p=19,97,127,487时的情况。可以注意到x xx要么没有对应的y yy值,要么有两个对应的y yy值,且这两个y yy值是对于y = p / 2 y=p/2y=p/2对称的。
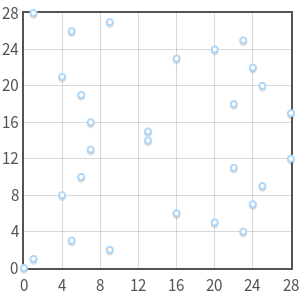
上图为有限域上面的奇异曲线的例子,即3 a 3 + 27 b 2 = 0 3a^3+27b^2=03a3+27b2=0的情况,这里的例子是y 2 ≡ x 3 ( m o d 29 ) y^2\equiv x^3 \pmod{29}y2≡x3(mod29)的情况,可以看到有一个奇异点( 0 , 0 ) (0,0)(0,0),所以这不是一个有效的椭圆曲线。
点之间的加法(几何上)
在实数上面,我们定义加法为三个一条直线上面的点的和为零( P + Q + R = 0 ) (P+Q+R=0)(P+Q+R=0),在有限域F p \mathbb{F}_pFp上面也可以这么定义,但是怎么理解有限域上面的在一条直线上呢?
显然,这条直线和实数上面的直线是不一样的。在实数上面我们定义满足同一个a x + b y + c = 0 ax+by+c=0ax+by+c=0关系式的点是在一条直线上面。那么类似的,我们在有限域F p \mathbb{F}_pFp上面可以定义a x + b y + c ≡ 0 ( m o d p ) ax+by+c\equiv 0 \pmod pax+by+c≡0(modp)上面的点在一条直线上面。
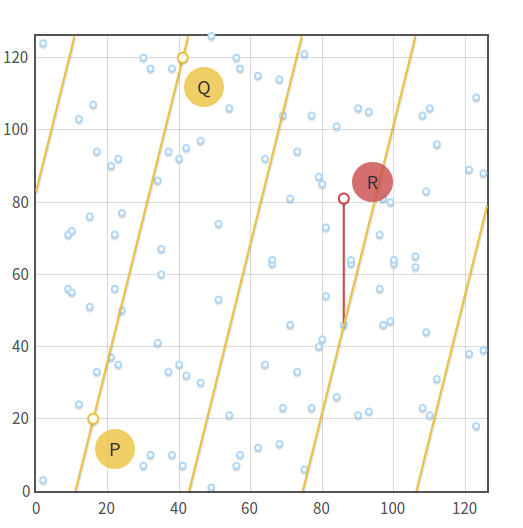
上图的椭圆曲线为y 2 ≡ x 3 − x + 3 ( m o d 127 ) y^2 \equiv x^3-x+3\pmod{127}y2≡x3−x+3(mod127),其中P = ( 16 , 20 ) , Q = ( 41 , 120 ) P=(16,20),Q=(41,120)P=(16,20),Q=(41,120)。直线为y ≡ 4 x + 83 ( m o d 127 ) y \equiv 4x + 83 \pmod{127}y≡4x+83(mod127)。
这样的加法仍然是满足群的性质的:
- Q + 0 = 0 + Q = Q Q+0=0+Q=QQ+0=0+Q=Q,0 00是单位元。
- 逆元的定义为Q = ( x Q , y Q ) m o d p Q=(x_Q,y_Q) \bmod pQ=(xQ,yQ)modp,− Q = ( x Q , − y Q ) m o d p -Q=(x_Q,-y_Q) \bmod p−Q=(xQ,−yQ)modp,比如F 29 \mathbb{F}_{29}F29中点Q = ( 2 , 5 ) Q=(2,5)Q=(2,5)的逆元为− Q = ( 2 , 24 ) -Q=(2,24)−Q=(2,24)。
- P+(-P)=0。
遗憾的是,这样的0 00并不能给出几何上面的解释。
点之间的加法(代数上)
在F p \mathbb{F}_pFp中计算加法和R \mathbb{R}R中的计算方法是一致的,除了要模p pp。
那么,给定P = ( x P , y P ) , Q = ( x Q , y Q ) P=(x_P,y_P),Q=(x_Q,y_Q)P=(xP,yP),Q=(xQ,yQ),以及R = ( x R , y R ) R=(x_R,y_R)R=(xR,yR),那么可以按如下方法计算P + Q = − R P+Q=-RP+Q=−R:
x R = ( m 2 − x P − x Q ) m o d p y R = [ y P + m ( x R − x P ) ] m o d p = [ y Q + m ( x R − x Q ) ] m o d p \begin{aligned} x_{R} &=\left(m^{2}-x_{P}-x_{Q}\right) \bmod p \\ y_{R} &=\left[y_{P}+m\left(x_{R}-x_{P}\right)\right] \bmod p \\ &=\left[y_{Q}+m\left(x_{R}-x_{Q}\right)\right] \bmod p \end{aligned}xRyR=(m2−xP−xQ)modp=[yP+m(xR−xP)]modp=[yQ+m(xR−xQ)]modp
如果P ≠ Q P\ne QP=Q,那么m = ( y P − y Q ) ( x P − x Q ) − 1 m o d p m=\left(y_{P}-y_{Q}\right)\left(x_{P}-x_{Q}\right)^{-1} \bmod pm=(yP−yQ)(xP−xQ)−1modp。
如果P = Q P=QP=Q,那么m = ( 3 x P 2 + a ) ( 2 y P ) − 1 m o d p m=\left(3 x_{P}^{2}+a\right)\left(2 y_{P}\right)^{-1} \bmod pm=(3xP2+a)(2yP)−1modp。
椭圆曲线的阶:
有限域上面的椭圆曲线是由有限个点所构成的,那么具体有几个点呢?
首先,定义概念椭圆曲线群的阶为当前椭圆曲线群上面的点的数量。
可以直接将x xx从0 00到p − 1 p-1p−1计数有多少点,但这样的复杂度是O ( p ) O(p)O(p)的,在p pp比较大的时候会很慢,也有比较高效的算法来计算椭圆曲线的阶,比如Schoof算法,这里不具体展开。
标量乘法以及循环群
标量乘法的计算方法即为计算多次的加法:
n P = P + P + ⋯ + P ⏟ n times n P=\underbrace{P+P+\cdots+P}_{n \text { times }}nP=n times P+P+⋯+P
同样的,可以用之前提出的二进制分解的方法来加快运算。
但有限域上面的乘法有一个有趣的性质,就是他会构成一个乘法循环子群。

拿y 2 = x 3 + 2 x + 3 ( m o d 97 ) y^2=x^3+2x+3 \pmod {97}y2=x3+2x+3(mod97)来举例,P = ( 3 , 6 ) P=(3,6)P=(3,6)的话,会发现n P nPnP会在( 0 , P , 2 P , 3 P , 4 P ) (0,P,2P,3P,4P)(0,P,2P,3P,4P)这些值中不断循环。可以在这个链接里面试一下。
这样的P PP被称作这个循环子群的生成元(generator)或者基本点(base point)。
子群的阶
有一个问题就是由P PP生成的循环子群的阶是多少呢?。或者换一种说法,P PP的阶是多少?。
- P PP的阶就是令n P = 0 nP=0nP=0的最小的n nn,(0 00本身除外),在上面的例子里面就是5 55。
- P PP的阶和整个椭圆曲线的阶是满足拉格朗日定理的,也就是说子群的阶可以整除父群的阶。
因此就可以用下面的方法找出某个点P PP的阶了:
- 使用Schoof算法计算得出整个椭圆曲线的阶N NN。
- 找到阶N NN的所有因子。
- 对于N NN的每个因子n nn,按照从小到大的方式,计算n P nPnP。
- 如果n P = 0 nP=0nP=0,那么n nn是子群的阶。
特例是如同y 2 = x 3 − x + 1 ( m o d 29 ) y^2=x^3-x+1 \pmod{29}y2=x3−x+1(mod29)这样的阶为素数37 3737的曲线,那么他的子群就是本身。也就是这个一个循环群。
如何找生成元
在椭圆曲线密码学中,我们需要一个较高次数的子群。所以一般来说,是先取一个曲线,然后计算他的阶N NN,选择一个比较大的因子n nn,然后根据这个因子来找到一个合适的生成元。
首先,介绍一下cofactor的概念,因此拉格朗日定理的存在,所以可以推断h = N / n h=N/nh=N/n是一个整数,那么这个h hh就是子群的cofactor。
那么对于曲线中的任意一个点,满足N P = 0 NP=0NP=0,也可以写成是n ( h P ) = 0 n(hP)=0n(hP)=0。
当n nn为素数时,只要任取一点P PP,令G = h P G=hPG=hP,那么G GG就是一个阶为n nn的生成元。
总结一下找生成元的步骤:
- 计算椭圆曲线的阶N NN。
- 选择某个因子n nn作为子群的阶。
- 计算cofactor h = N / n h=N/nh=N/n。
- 选择曲线上面随机一个点P PP。
- 计算G = h P G=hPG=hP。
- 如果G = 0 G=0G=0,那么从第四步开始重新选,否则G GG就是我们要的生成元了。
椭圆曲线上面的离散对数问题
在有限域的椭圆曲线中,其离散对数问题定义为:
如果知道P PP和Q QQ,那么如何找到一个k kk使得Q = k P Q=kPQ=kP?。
这样一个问题是一个标准的密码学难题假设,也就是大家公认这个问题是比较困难的。
而那些基于整数群上面的离散对数问题的算法比如DSA或者Diffle-Hellman以及Elgamal,都有其在椭圆曲线上面的平替。
椭圆曲线一个优秀的性质在于,同样对于整数上面的离散对数问题b = a k m o d p b=a^k \bmod pb=akmodp,在参数大小相同的情况下,椭圆曲线的离散对数问题更难解决。
因此,要达到同样的安全等级,椭圆曲线的参数大小更小。