曲率的计算公式

1. 连续曲线计算

利用一阶导和二阶导，求曲率 （不适用与离散点）

连续曲线求曲率

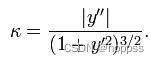
 2.  离散点最小二乘拟合圆

最小二乘拟合圜

3. 三个离散点求外接圆， 海伦-秦九韶公式

核心公式： 海伦公式 + 面积公式

a*b*c = 4 * R * S

方法一：海伦-秦九韶公式

三边是a,b,c
令p=(a+b+c)/2
则S=√[p(p-a)(p-b)(p-c)]

方法二：海伦公式

s＝√[p﹙p-a)(p-b)(p-c)]
p=½(a+b+c)

推导如下：

这是海伦公式
假设有一个三角形，边长分别为a、b、c，三角形的面积S可由以下公式求得：
S=√[p(p-a)(p-b)(p-c)]
而公式里的p为半周长：
p=(a+b+c)/2
设三角形的三边a、b、c的对角分别为A、B、C，则余弦定理为
cosC = (a^2+b^2-c^2)/2ab

S=1/2*ab*sinC
=1/2*ab*√(1-cos^2 C)
=1/2*ab*√[1-(a^2+b^2-c^2)^2/4a^2*b^2]
=1/4*√[4a^2*b^2-(a^2+b^2-c^2)^2]
=1/4*√[(2ab+a^2+b^2-c^2)(2ab-a^2-b^2+c^2)]
=1/4*√[(a+b)^2-c^2][c^2-(a-b)^2]
=1/4*√[(a+b+c)(a+b-c)(a-b+c)(-a+b+c)]

设p=(a+b+c)/2
则p=(a+b+c)/2, p-a=(-a+b+c)/2, p-b=(a-b+c)/2,p-c=(a+b-c)/2,

上式=√[(a+b+c)(a+b-c)(a-b+c)(-a+b+c)/16]
=√[p(p-a)(p-b)(p-c)]
所以，三角形ABC面积S=√[p(p-a)(p-b)(p-c)]

海伦公式计算曲率

离散点计算曲率

三个点外接圆面积S 矩阵

三个点向量叉积计算面积