目录
深度优先遍历(DFS)和广度优先遍历(BFS)原理
1、自己的原理图
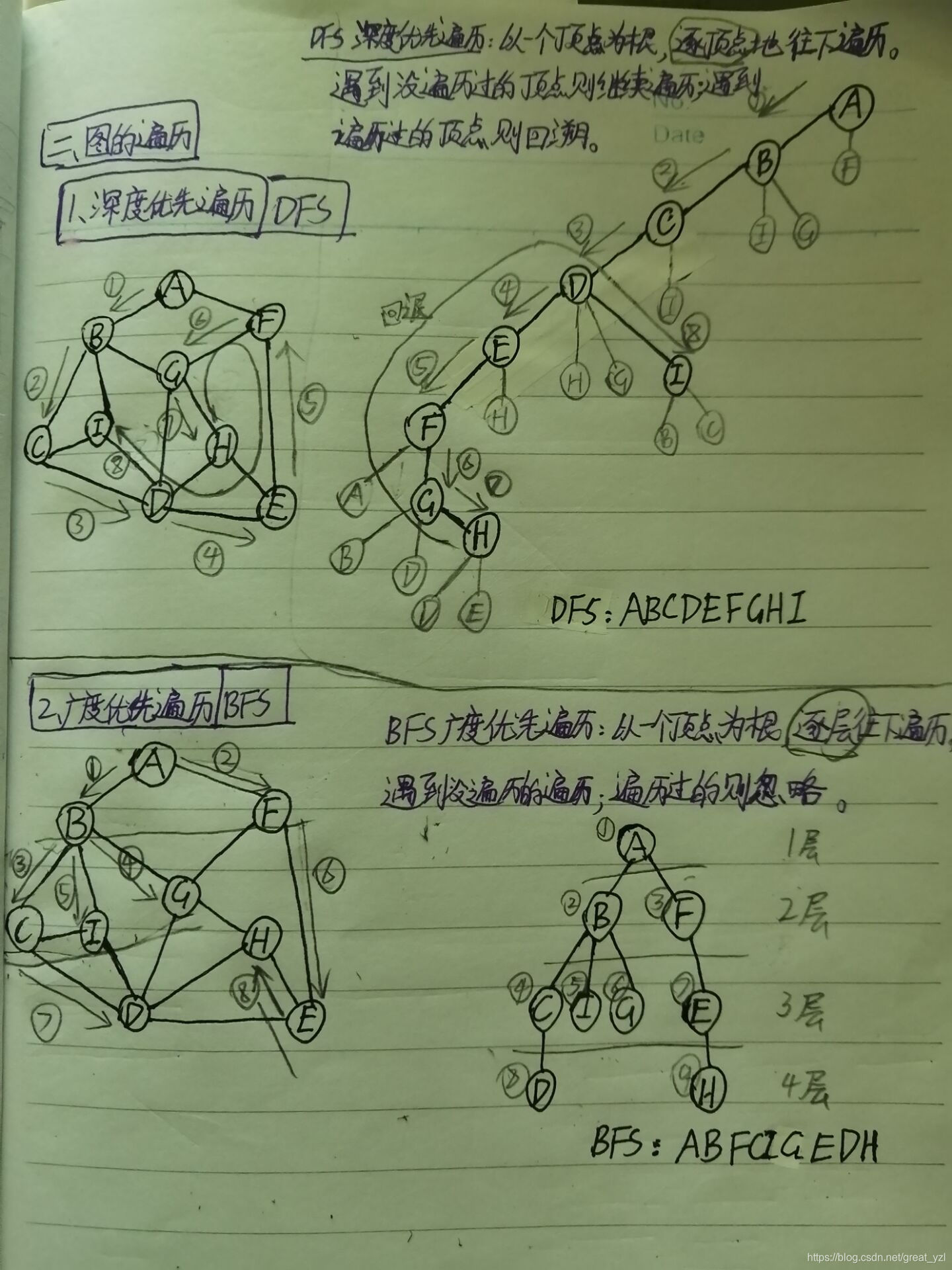
2、官方原理图
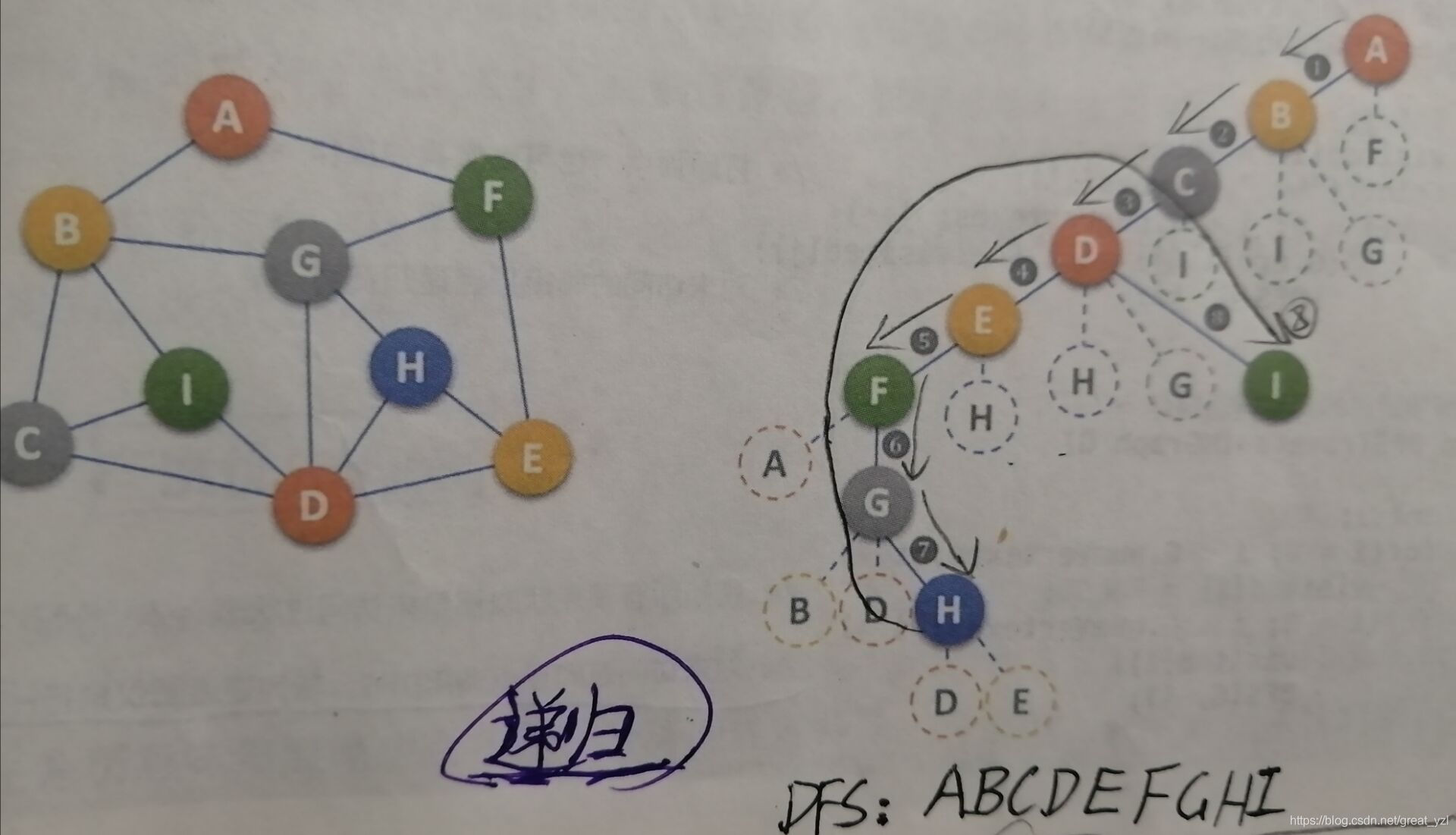
DFS(深度优先遍历): 以一个顶点为根,逐顶点地往下遍历,遇到没遍历过的顶点则继续遍历;遇到遍历过的顶点则回溯。(递归实现)
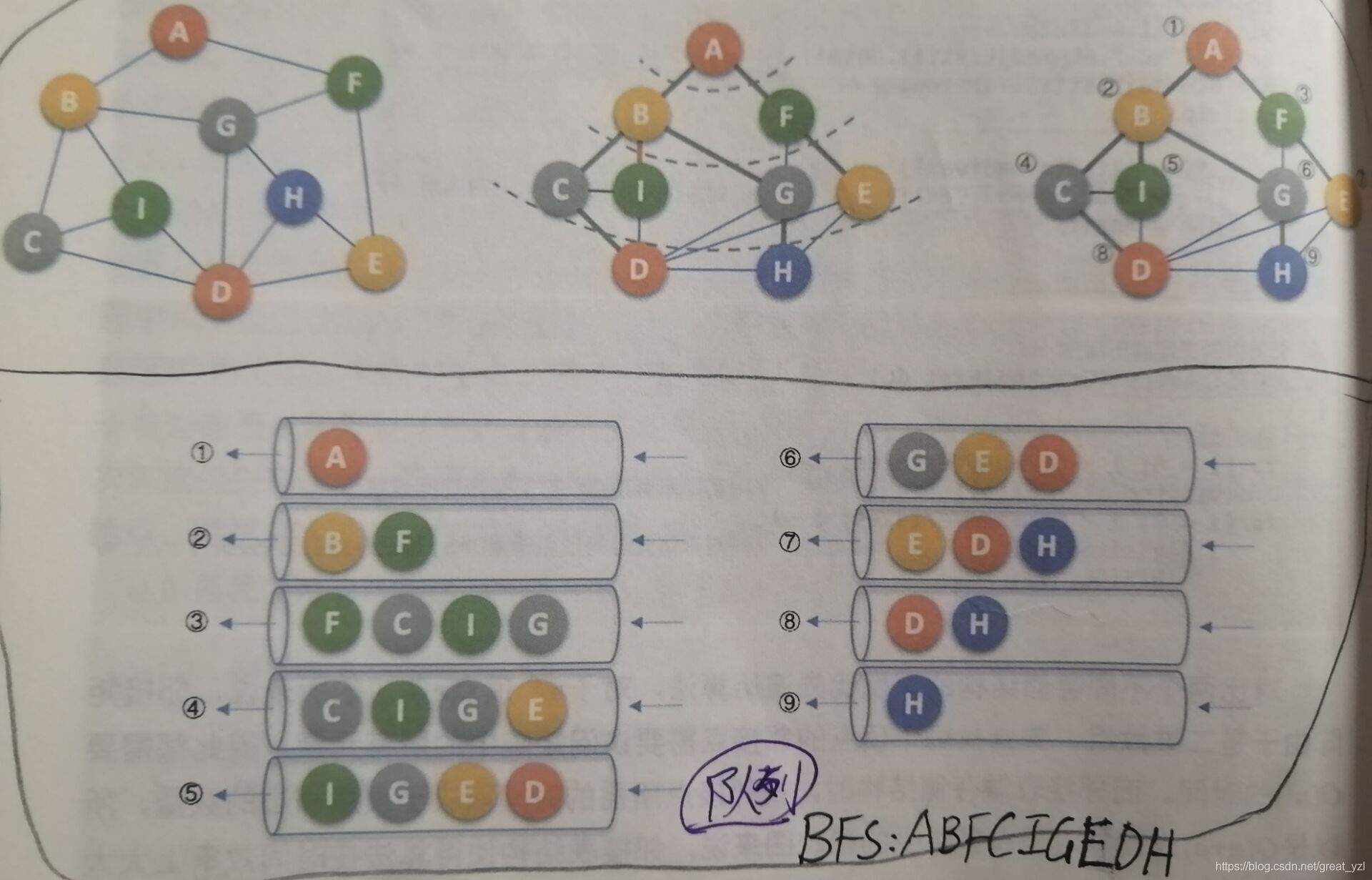
BFS(广度优先遍历):以一个顶点为根,逐层地往下遍历,遇到遍历的顶点遍历;遍历过的顶点则忽略。(队列实现)
一、邻接矩阵的深度优先遍历(DFS)
1、原理图
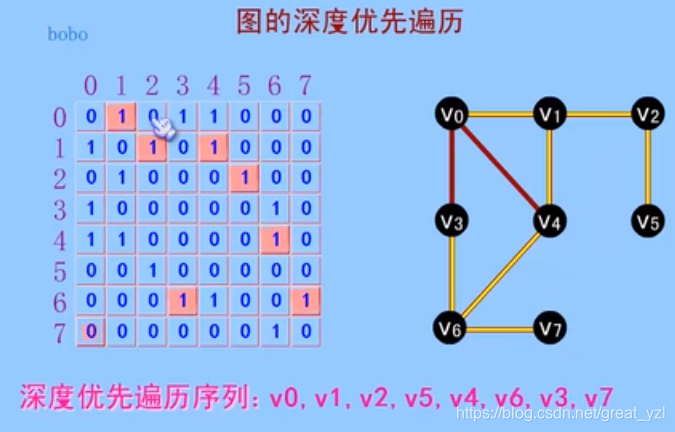
2、 过程:
1、矩阵形式的话,先从根开始走,遇到0就继续,遇到1直接跳到那一行(即跳到那一个元素),后面如此往复,用递归实现。
2、还有就是需要判断结点是否已经遍历过了,已经遍历过的结点不再进入,由于每一列都是同一结点(待遍历),可以通过一个判断数组记录每一个元素是否遍历。
//深度优先遍历
void DFS(int index)
{
int i, j;
for (i = index; i < G.vertexNum; i++)
{
for (j = 0; j < G.vertexNum; j++)
{
if (i == 0 && j == 0)
{
printf("%c", G.vertex[j]); //输出首元素(根)
Judge[j] = 1; //标记首列
}
if (G.edge[i][j] != 0 && Judge[j] == 0) //邻接矩阵有元素;且01数组无标记(即未被访问)
{
printf("%c", G.vertex[j]);
if (Judge[j] == 0) //未标记
Judge[j] = 1; //对列做标记
DFS(j);
}
}
}
}3、总代码
//图的深度优先遍历(邻接矩阵)
//需要创建一个列数组,按照矩阵的顺序遍历,为1就直接跳到那个结点
//增添一个数组,判断每个结点是否遍历过
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#define MAXSIZE 20
int ColumnArray[MAXSIZE]; //列矩阵(判断有没有走过)
//邻接矩阵
typedef struct
{
char vertex[MAXSIZE]; //顶点
int edge[MAXSIZE][MAXSIZE]; //邻接顶点
int vertexNum; //顶点数量
}Graph;
Graph G;
//输入顶点
void InputVertex()
{
int i = 0;
char ch;
printf("请输入需要创建的图顶点(不需要空格):\n");
do
{
scanf("%c", &ch);
if (ch != '\n')
G.vertex[i++] = ch;
} while (ch != '\n');
G.vertexNum = i;
}
//查找(根据结点找索引)
int findIndex(char ch)
{
int i;
for (i = 0; i < G.vertexNum; i++)
{
if (G.vertex[i] == ch)
return i;
}
return -1; //没找到
}
//创建图
void InputEdge()
{
int i, index;
char ch;
for (i = 0; i < G.vertexNum; i++)
{
printf("请输入%c指向的邻接结点:\n", G.vertex[i]);
scanf("%c", &ch);
while (ch != '\n')
{
index = findIndex(ch); //查找输入结点的索引
G.edge[i][index] = 1;
scanf("%c", &ch);
}
}
}
//01数组初始化
void InitColumnArray()
{
int j;
for (j = 0; j < G.vertexNum; j++)
ColumnArray[j] = 0; //标记未访问
}
//输出测试
void Print()
{
int i, j;
for (i = 0; i < G.vertexNum; i++)
{
printf("\n%c结点的邻接结点为:\t", G.vertex[i]);
for (j = 0; j < G.vertexNum; j++)
{
if (G.edge[i][j] != 0)
printf("%c\t", G.vertex[j]);
}
}
}
//深度优先遍历
void DeepTraverse(int index)
{
int i, j;
for (i = index; i < G.vertexNum; i++)
{
for (j = 0; j < G.vertexNum; j++)
{
if (i == 0 && j == 0)
{
printf("%c", G.vertex[j]); //输出首元素(根)
ColumnArray[j] = 1; //标记首列
}
if (G.edge[i][j] != 0 && ColumnArray[j] == 0) //邻接矩阵有元素;且01数组无标记(即未被访问)
{
printf("%c", G.vertex[j]);
if (ColumnArray[j] == 0) //未标记
ColumnArray[j] = 1; //对列做标记
DeepTraverse(j);
}
}
}
}
int main()
{
//创建图
InputVertex();
InputEdge();
InitColumnArray();
printf("深度优先遍历结果:\n");
//深度优先遍历
DeepTraverse(0);
//输出测试
//Print();
return 0;
}二、邻接表的深度优先遍历(DFS):
1、原理图:
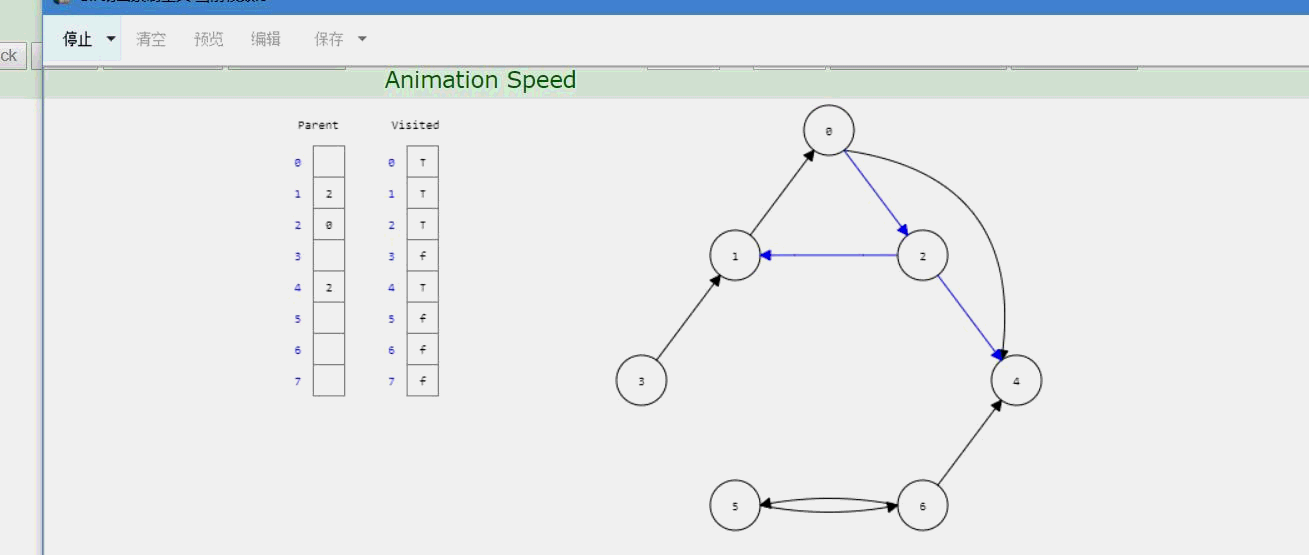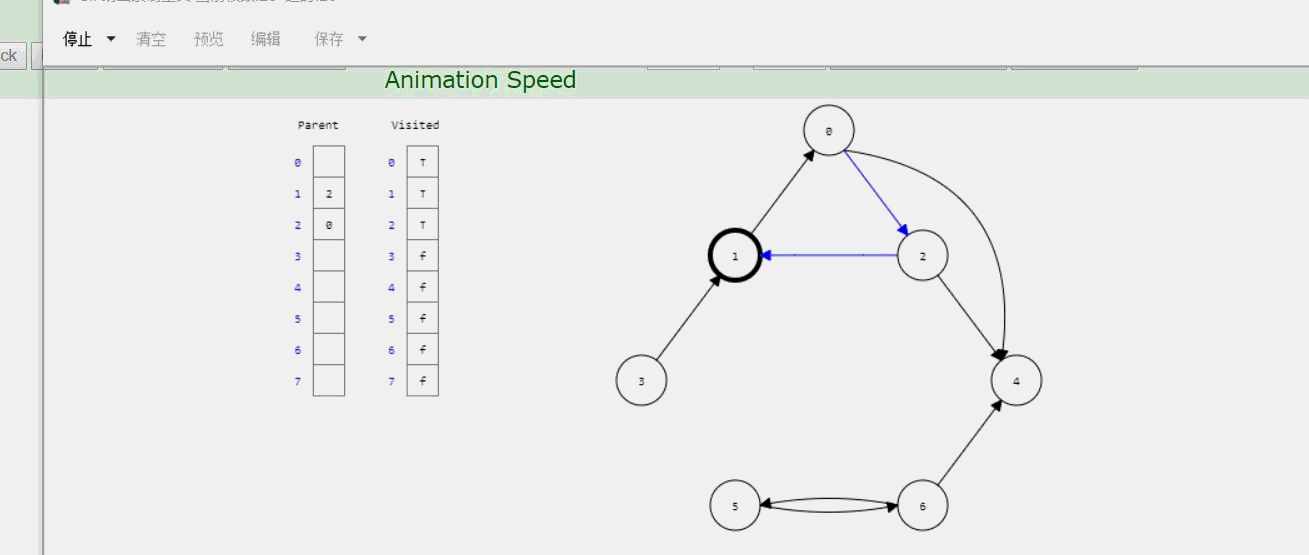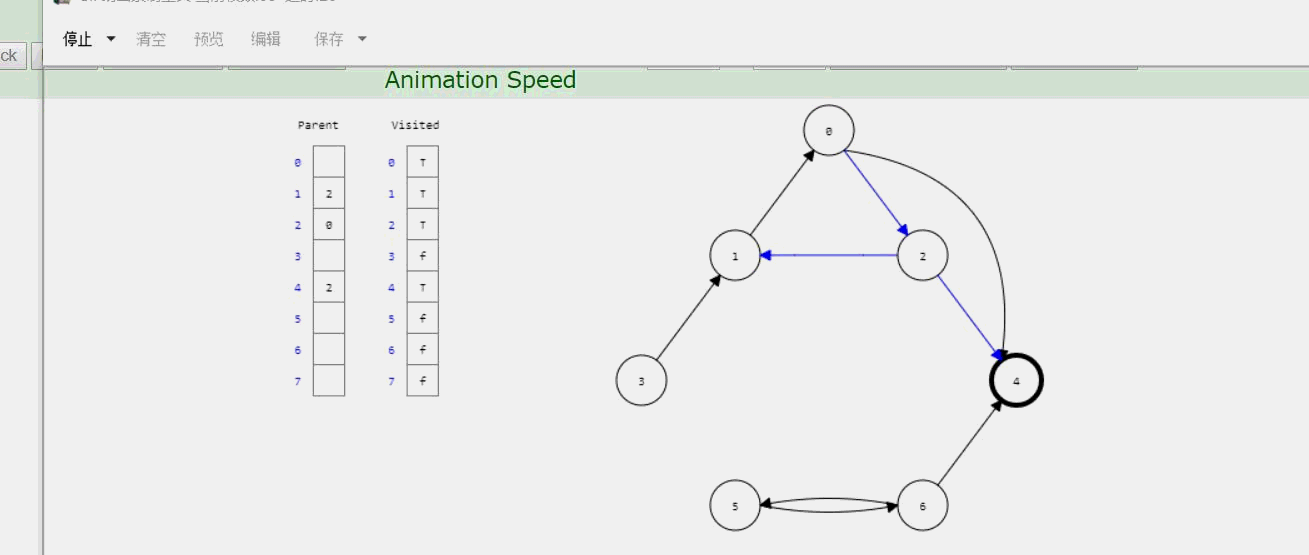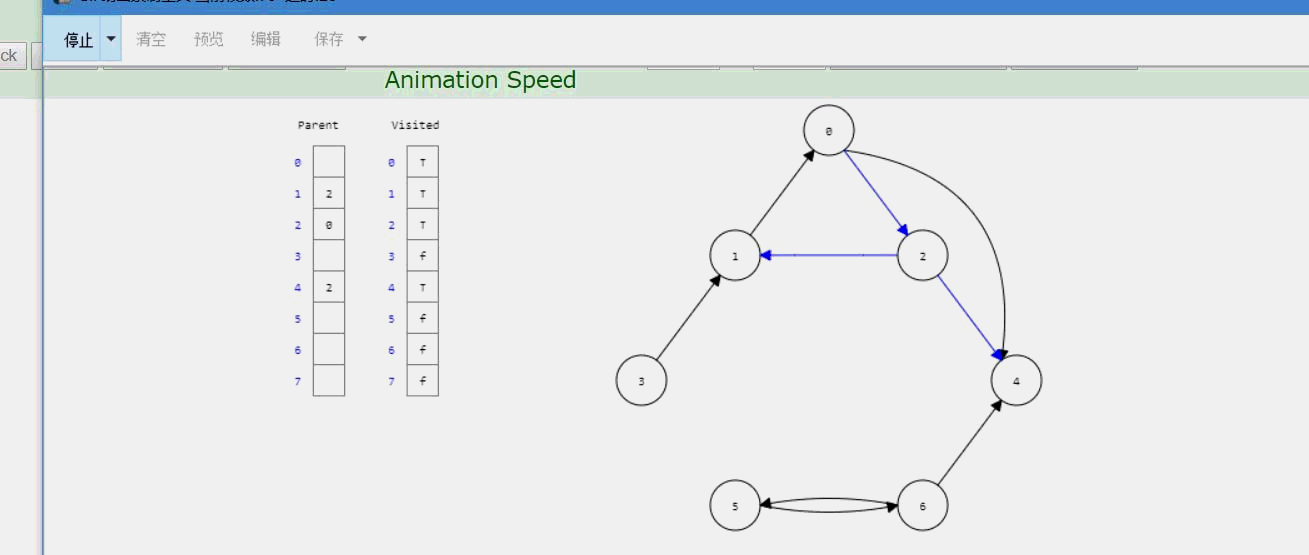
2、过程
和邻接矩阵类似,也是使用递归,也是需要用一个判断数组,表示每个顶点的邻接矩阵是否遍历过。只不过邻接表需要传一个参数lastIndex,利用这个参数把根结点输出出去。先把指针指向firstchild,后面利用一个while循环挨个判断邻接结点是否遍历过了,遍历过则指针继续后移;未遍历过则递归调用DFS函数进入那个未遍历的顶点,继续一个一个判断。
//深度优先遍历(按顶点操作)
//判断的时候需要遍历每一个邻接顶点,而输出的时候只需要把顶点数组的内容输出即可
void DFS(EdgeNode* p1, int lastIndex)
{
if (Judge[lastIndex] == 0) //顶点未遍历
{
Judge[lastIndex] = 1; //标记(表示遍历过)
printf("%c", V[lastIndex].data); //输出根顶点(保存lastIndex目的就是便于追溯到顶点数组,把根顶点输出)
//开始遍历后面的邻接顶点
while (p1 != NULL)
{
if (Judge[p1->index] == 0) //未遍历(遍历每一个顶点)
{
DFS(V[p1->index].firstEdge, p1->index); //递归深度优先遍历(输出只需要把顶点数组的东西输出即可)
}
p1 = *(p1->next); //后移(遍历每一个邻接顶点)
}
}
}3、总代码
//邻接表的深度优先遍历(DFS)
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 20
int length = 0; //顶点数组长度
int Judge[MAXSIZE]; //列矩阵(记录顶点是否已遍历过)
//邻接顶点
typedef struct EdgeNode
{
char data;
int index;
struct EdgeNode** next; //二级指针
}EdgeNode, * pEdgeNode;
//顶点数组(结构体数组)
typedef struct Vertex
{
char data;
EdgeNode* firstEdge;
}Vertex;
Vertex V[MAXSIZE];
void Input()
{
int i;
char ch;
printf("请输入图的所有顶点:\n");
scanf("%c", &ch);
for (i = 0; i < MAXSIZE && ch != '\n'; i++)
{
V[i].data = ch;
scanf("%c", &ch);
}
length = i;
}
void InitVertex()
{
int i;
for (i = 0; i < length; i++)
{
V[i].firstEdge = NULL;
Judge[i] = 0; //列数组初始化
}
}
//根据字符查找在顶点数组中的下标
int FindIndex(char ch)
{
int i;
for (i = 0; i < length; i++)
{
if (ch == V[i].data)
return i;
}
return -1; //没找到
}
//创建图
void CreateGraph()
{
int i;
char ch;
pEdgeNode* p2 = NULL; //二级指针
for (i = 0; i < length; i++)
{
printf("\n请输入%c的邻接顶点:\t", V[i].data);
scanf("%c", &ch);
//首个顶点
if (ch != '\n')
{
V[i].firstEdge = (EdgeNode*)malloc(sizeof(EdgeNode)); //一级指针分配空间
p2 = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针分配空间
p2 = &V[i].firstEdge;
(*p2)->data = ch;
(*p2)->index = FindIndex(ch);
(*p2)->next = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针分配空间
*((*p2)->next) = NULL;
scanf("%c", &ch);
}
while (ch != '\n')
{
p2 = (*p2)->next; //向后传递
(*p2) = (EdgeNode*)malloc(sizeof(EdgeNode)); //一级指针分配空间
(*p2)->data = ch;
(*p2)->index = FindIndex(ch);
(*p2)->next = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针分配空间
*((*p2)->next) = NULL;
scanf("%c", &ch);
}
}
}
//深度优先遍历(按顶点操作)
//判断的时候需要遍历每一个邻接顶点,而输出的时候只需要把顶点数组的内容输出即可
void DFS(EdgeNode* p1, int lastIndex)
{
if (Judge[lastIndex] == 0) //顶点未遍历
{
Judge[lastIndex] = 1; //标记(表示遍历过)
printf("%c", V[lastIndex].data); //输出根顶点(保存lastIndex目的就是便于追溯到顶点数组,把根顶点输出)
//开始遍历后面的邻接顶点
while (p1 != NULL)
{
if (Judge[p1->index] == 0) //未遍历(遍历每一个顶点)
{
DFS(V[p1->index].firstEdge, p1->index); //递归深度优先遍历(输出只需要把顶点数组的东西输出即可)
}
p1 = *(p1->next); //后移(遍历每一个邻接顶点)
}
}
}
//输出测试
void Print()
{
int i;
EdgeNode* p1; //一级指针
for (i = 0; i < length; i++)
{
p1 = V[i].firstEdge;
while (p1 != NULL)
{
printf("%c", p1->data);
p1 = *(p1->next);
}
}
}
int main()
{
Input();
InitVertex();
CreateGraph(); //创建图
DFS(V[0].firstEdge ,0); //深度优先遍历(从首结点开始)
//Print();
}三、邻接矩阵的广度优先遍历
1、原理图
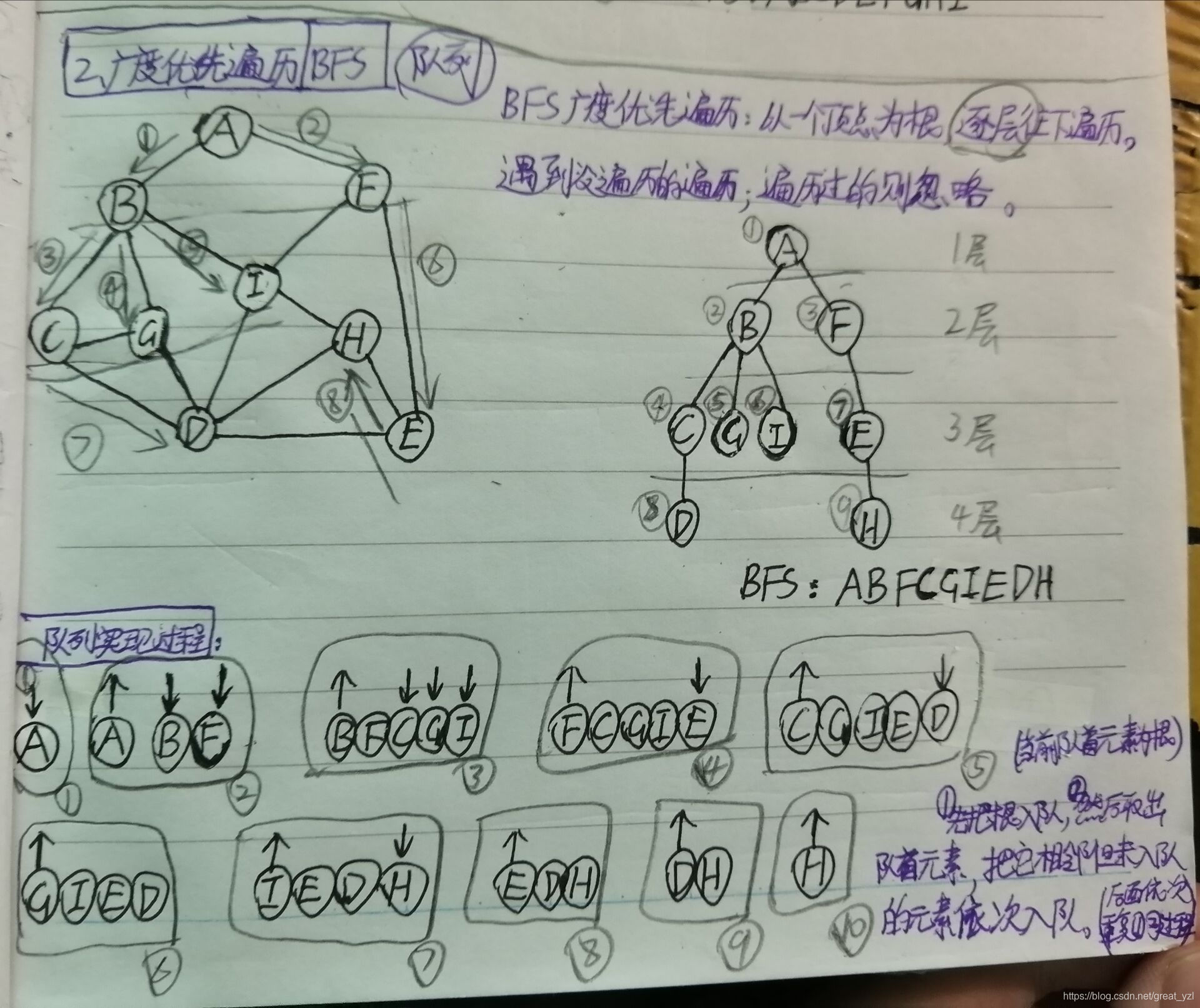
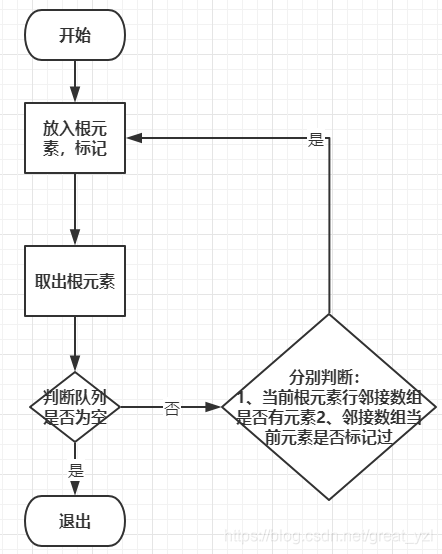
2、过程
先把根元素入队并标记,然后取出根元素,依次判断:1、当前根元素行邻接数组是否有元素;2、当前元素是否标记过-> 若有元素且未标记,则入队该元素并标记;否则跳过。然后调用BFS()函数进行递归,直到队列为空结束。(一个顶点一次循环判断入队)
1、入队首元素并标记 ,调用BFS()
EnQueue(0); //首元素入队
Judge[0] = 1; //标记首元素
BFS(DeQueue()); //广度优先遍历2、 BFS()函数
//广度优先遍历(BFS)
void BFS(int index)
{
int j;
printf("%c", G.vertex[index]); //输出
for (j = 0; j < G.length; j++)
{
if (G.edge[index][j] != 0 && Judge[j] == 0) //有邻接顶点且未入队
{
Judge[j] = 1; //标记
EnQueue(j); //入队
}
}
//遍历队列下一个元素
index = DeQueue(); //取出当前队首作为根
//判断队列是否为空,空则退出,非空则继续遍历
if (index == -1)
return;
else
BFS(index); //递归进行下一个元素的广度优先遍历
}3、总代码
//邻接矩阵的广度优先遍历
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#define MAXSIZE 20
int Judge[MAXSIZE] = { 0 };
//队列结构体
typedef struct
{
int rear;
int front;
int num[MAXSIZE]; //放入队列的序号
}Queue;
Queue Q;
//邻接矩阵结构体
typedef struct
{
char vertex[MAXSIZE]; //顶点数组
int edge[MAXSIZE][MAXSIZE]; //边数组
int length; //顶点数量
}Graph;
Graph G;
//输入顶点
void Input()
{
int i;
char ch;
printf("请输入全部顶点:\n");
scanf("%c", &ch);
for (i = 0; i < MAXSIZE && ch != '\n'; i++)
{
G.vertex[i] = ch;
scanf("%c", &ch);
}
G.length = i; //顶点数量
}
//初始化(邻接结点数组和队列)
void Init()
{
int i, j;
for (i = 0; i < G.length; i++)
{
for (j = 0; j < G.length; j++)
{
G.edge[i][j] = 0;
}
}
Q.rear = 0; //队尾
Q.front = 0; //队首
}
//入队
void EnQueue(int num)
{
Q.num[Q.rear++] = num;
}
//出队
int DeQueue()
{
if (Q.front == Q.rear)
return -1;
return Q.num[Q.front++];
}
//根据字符返回下标
int FindIndex(char ch)
{
int i;
for (i = 0; i < G.length; i++)
{
if (G.vertex[i] == ch)
return i;
}
return -1; //没找到
}
//创建图
void CreateGraph()
{
int i, index;
char ch;
for (i = 0; i < G.length; i++)
{
printf("\n请输入%c结点的邻接结点:\t", G.vertex[i]);
scanf("%c", &ch);
while (ch != '\n')
{
index = FindIndex(ch); //获取列下标(被指向元素下标)
G.edge[i][index] = 1;
scanf("%c", &ch);
}
}
}
//广度优先遍历(BFS)
void BFS(int index)
{
int j;
printf("%c", G.vertex[index]); //输出
for (j = 0; j < G.length; j++)
{
if (G.edge[index][j] != 0 && Judge[j] == 0) //有邻接顶点且未入队
{
Judge[j] = 1; //标记
EnQueue(j); //入队
}
}
//遍历队列下一个元素
index = DeQueue(); //取出当前队首作为根
//判断队列是否为空,空则退出,非空则继续遍历
if (index == -1)
return;
else
BFS(index); //递归进行下一个元素的广度优先遍历
}
//测试遍历
void Print()
{
int i, j;
for (i = 0; i < G.length; i++)
{
printf("\n%c邻接结点:\t", G.vertex[i]);
for (j = 0; j < G.length; j++)
printf("%d ", G.edge[i][j]);
}
}
int main()
{
Input();
Init();
CreateGraph();
EnQueue(0); //首元素入队
Judge[0] = 1; //标记首元素
printf("\n广度优先遍历:");
BFS(DeQueue()); //广度优先遍历
//Print();
return 0;
}四、邻接表的广度优先遍历(BFS)
原理和上面的邻接矩阵类似,以顶点为单位,往后判断是否有需要入队的元素(只用判断是否遍历过即可,因为接在顶点后面作为邻接顶点,必然是邻接顶点,所以不需要再像数组那样判断是否为邻接顶点)。
1、首调用BFS
EnQueue(0); //入队首元素
Judge[0] = 1; //判断
BFS(DeQueue()); //广度优先遍历并出队队首元素2、BFS()
//广度优先遍历
void BFS(int index)
{
int i;
EdgeNode* p;
printf("%c", G[index].vertex); //输出顶点
p = G[index].firstEdge; //指向顶点首指针
while (p)
{
if (Judge[p->index] == 0)
{
Judge[p->index] = 1; //标记
EnQueue(p->index); //入队
}
p = *(p->next); //后移
}
if (Q.front == Q.rear) //队列为空
return;
else
BFS(DeQueue()); //广度优先遍历并出队队首元素
}总代码
//邻接表的广度优先遍历
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 20
int length; //记录顶点数组长度
int Judge[MAXSIZE] = { 0 };
//邻接顶点结构体
typedef struct EdgeNode
{
char data; //存放数据
int index; //数据在顶点结构体中的下标
struct EdgeNode** next; //二级指针
}EdgeNode, *pEdgeNode;
//顶点结构体
typedef struct
{
char vertex;
EdgeNode* firstEdge; //一级指针(指向首个邻接顶点)
}Graph;
Graph G[MAXSIZE];
//队列结构体
typedef struct
{
int num[MAXSIZE]; //存放顶点下标
int front; //队首
int rear; //队尾
}Queue;
Queue Q;
//输入顶点数组
void InputVertex()
{
int i;
char ch;
printf("请输入所有顶点:\n");
scanf("%c", &ch);
for (i = 0; i < MAXSIZE && ch != '\n'; i++)
{
G[i].vertex = ch;
scanf("%c", &ch);
}
length = i; //顶点数组长度
}
//初始化(*firstEdge和队列初始化)
void Init()
{
int i;
for (i = 0; i < length; i++)
{
G[i].firstEdge = NULL;
}
Q.front = 0; //队首
Q.rear = 0; //队尾
}
//入队
void EnQueue(int num)
{
Q.num[Q.rear++] = num;
}
//出队
int DeQueue()
{
return Q.num[Q.front++];
}
//根据数据查找下标
int FindIndex(char ch)
{
int i;
for (i = 0; i < length; i++)
{
if (ch == G[i].vertex)
return i;
}
return -1;
}
//创建邻接顶点链表
void CreateEdge()
{
int i;
char ch;
pEdgeNode* p2=NULL; //二级指针
for (i = 0; i < length; i++)
{
printf("请输入%c顶点的邻接顶点:\t", G[i].vertex);
scanf("%c", &ch);
//首个顶点
if (ch != '\n')
{
G[i].firstEdge = (EdgeNode*)malloc(sizeof(EdgeNode)); //一级指针
p2 = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针
p2 = &G[i].firstEdge; //连接首指针
(*p2)->data = ch;
(*p2)->index = FindIndex(ch);
(*p2)->next = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针
*((*p2)->next) = NULL; //尾指针地址赋空
scanf("%c", &ch);
}
//后面的顶点
while (ch != '\n')
{
p2 = (*p2)->next;
(*p2)= (EdgeNode*)malloc(sizeof(EdgeNode)); //一级指针
(*p2)->next = (pEdgeNode*)malloc(sizeof(pEdgeNode)); //二级指针
(*p2)->data = ch;
(*p2)->index = FindIndex(ch);
*((*p2)->next) = NULL;
scanf("%c", &ch);
}
}
}
//广度优先遍历
void BFS(int index)
{
int i;
EdgeNode* p;
printf("%c", G[index].vertex); //输出顶点
p = G[index].firstEdge; //指向顶点首指针
while (p)
{
if (Judge[p->index] == 0)
{
Judge[p->index] = 1; //标记
EnQueue(p->index); //入队
}
p = *(p->next); //后移
}
if (Q.front == Q.rear) //队列为空
return;
else
BFS(DeQueue()); //广度优先遍历并出队队首元素
}
//测试输出
void Print()
{
int i;
EdgeNode* p;
for (i = 0; i < length; i++)
{
p = G[i].firstEdge;
printf("\n%c的邻接顶点为:\t", G[i].vertex);
while (p != NULL)
{
printf("%c", p->data);
p = *(p->next);
}
}
}
int main()
{
InputVertex(); //输入顶点
Init(); //初始化
CreateEdge(); //创建邻接顶点链表
printf("\n广度优先遍历:\t");
EnQueue(0); //入队首元素
Judge[0] = 1; //判断
BFS(DeQueue()); //广度优先遍历并出队队首元素
//Print(); //测试输出
return 0;
}才疏学浅,有些地方可能会有点错误的地方,还望大家斧正,Thanks♪(・ω・)ノ
版权声明:本文为great_yzl原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。
