javascript安全计算
在正常的数学逻辑思维中,0.1+0.2=0.3这个逻辑是正确的,但是在JavaScript中0.1+0.2!==0.3,这是为什么呢?这个问题也会偶尔被用来当做面试题来考查面试者对JavaScript的数值的理解程度。
在JavaScript中的二进制的浮点数0.1和0.2并不是十分精确,在他们相加的结果并非正好等于0.3,而是一个比较接近的数字 0.30000000000000004 ,所以条件判断结果为false。
浮点数计算出现问题的原因
和其它语言如 Java 和 Python 不同,JavaScript 中所有数字包括整数和小数都只有一种类型 — Number。它的实现遵循 IEEE 754 标准,使用 64 位固定长度来表示,也就是标准的 double 双精度浮点数(相关的还有float 32位单精度)。
这样的存储结构优点是可以归一化处理整数和小数,节省存储空间。
64位比特又可分为三个部分:
- 符号位S:第 1 位是正负数符号位(sign),0代表正数,1代表负数
- 指数位E:中间的 11 位存储指数(exponent),用来表示次方数
- 尾数位M:最后的 52 位是尾数(mantissa),超出的部分自动进一舍零

实际上数字可以用以下公式表示: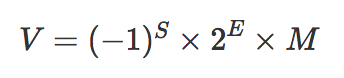
首先,我们要站在计算机的角度思考 0.1 + 0.2 这个看似小儿科的问题。我们知道,能被计算机读懂的是二进制,而不是十进制,所以我们先把 0.1 和 0.2 转换成二进制看看:
0.1 => 0.0001 1001 1001 1001…(无限循环)
0.2 => 0.0011 0011 0011 0011…(无限循环)
双精度浮点数的小数部分最多支持 52 位,所以两者相加之后得到这么一串 0.0100110011001100110011001100110011001100110011001100
这时候,我们再把它转换为十进制,就成了
0.30000000000000004。
为什么 x=0.1 能得到 0.1?
因为 mantissa 固定长度是 52 位,再加上省略的一位,最多可以表示的数是 2^53=9007199254740992,对应科学计数尾数是 9.007199254740992,这也是 JS 最多能表示的精度。它的长度是 16,所以可以使用 toPrecision(16) 来做精度运算,超过的精度会自动做凑整处理。于是就有:
0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000,去掉末尾的零后正好为 0.1
// 但你看到的 `0.1` 实际上并不是 `0.1`。可用更高的精度试试:
0.1.toPrecision(21) = 0.100000000000000005551
浮点数计算的解决办法
在淘宝早期的订单系统中把订单号当作数字处理,后来随意订单号暴增,已经超过了
9007199254740992,最终的解法是把订单号改成字符串处理。
toPrecision vs toFixed
数据处理时,这两个函数很容易混淆。它们的共同点是把数字转成字符串供展示使用。注意在计算的中间过程不要使用,只用于最终结果。
不同点就需要注意一下:
- toPrecision 是处理精度,精度是从左至右第一个不为0的数开始数起。
- toFixed 是小数点后指定位数取整,从小数点开始数起。
- 两者都能对多余数字做凑整处理,也有些人用 toFixed 来做四舍五入,但一定要知道它是有 Bug 的。
如:1.005.toFixed(2) 返回的是 1.00 而不是 1.01。
原因: 1.005 实际对应的数字是 1.00499999999999989,在四舍五入时全部被舍去!
解法:使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行,因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。
要想解决大数的问题,可以用以下几种方法:
使用github上的库:BigDecimal.js或bignumber.js
原理是把所有数字当作字符串,重新实现了计算逻辑,缺点是性能比原生的差很多。所以原生支持大数就很有必要了,现在 TC39 已经有一个 Stage 3 的提案 proposal bigint,大数问题有望彻底解决。
在浏览器正式支持前,可以使用 Babel 7.0 来实现,它的内部是自动转换成 big-integer 来计算,要注意的是这样能保持精度但运算效率会降低
//加法(四舍五入保留两位小数):
var a = new BigDecimal("2.555555").add(new BigDecimal("5.222222")).setScale(2, MathContext.ROUND_HALF_UP).toString();
//减法
new BigDecimal("2.40").subtract(new BigDecimal("2"))
//乘法:
new BigDecimal("2.40").multiply(new BigDecimal("2"))
//除法:
new BigDecimal("2.40").divide(new BigDecimal("2"), def)
使用简单点四舍五入方法,其实跟上面的方法差不多,只不过取了一个12位小数。
function numTofixed(num) {
if (typeof num == 'number') {
num = parseFloat(num.toFixed(12))
}
return num;
}
numTofixed(0.1 + 0.2);
function strip(num, precision = 12) {
return +parseFloat(num.toPrecision(precision));
}
strip(0.1 + 0.2,precision = 12);
为什么选择 12 做为默认精度?这是一个经验的选择,一般选12就能解决掉大部分0001和0009问题,而且大部分情况下也够用了,如果你需要更精确可以调高。
小数转成整数来处理
function add(num1, num2) {
const num1Digits = (num1.toString().split('.')[1] || '').length;
const num2Digits = (num2.toString().split('.')[1] || '').length;
const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
return (num1 * baseNum + num2 * baseNum) / baseNum;
}
将小数取整之后再进行运算。
通过正则来处理
function fixFloatCalcRudely(num){
if(typeof num == 'number'){
var str=num.toString(),
match=str.match(/\.(\d*?)(9|0)\2{5,}(\d{1,5})$/);
if(match != null){
return num.toFixed(match[1].length)-0;
}
}
return num;
}
利用正则取到匹配到的第一个小数,再进行运算。