跳石头（二分+贪心）

原题TP

输入格式

输出格式
一个整数，即最短跳跃距离的最大值。

输入

25 5 2
2
11
14
17
21

输出

4

说明/提示
样例数据说明：将与起点距离为 2和 14的两个岩石移走后,最短的跳跃距离为 4(从与起点距离 17 的岩石跳到距离 21 的岩石,或者从距离 21的岩石跳到终点)。
另外：全部数据满足如下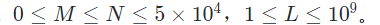

分析

1.此题按照暴力解的意思，就是依次采取距离（1~L），从所有石头中找出到源点之间有多少个石头可以删除，且删除数量不超过要求的数量M，找到移除石头数量恰好满足题意，且不超过不少于题述的那个临界距离就是答案。
2.用二分主要是可以优化时间复杂度，更快找到那个距离，从而不超时，二分的策略见注释。

代码（可左右滑动）

#include<bits/stdc++.h>
using namespace std;
//最短最长、最大最小这些问题通常用二分来解决，   二分需要满足： 有界性和单调性 
int N,M,L;
int ans;  //最终答案
int a[100010];

int check(int x){
	int t = 0;  //记录初始距离
	int rm = 0; //记录移除的石头数量 
	for(int i = 0 ; i < N ; ++i){
		if(a[i] - t < x){  //< 才删掉， = 是符合的。 
			rm++;
		}else{
			t = a[i]; //没有移除，当前位置为下一次判断的初始距离。 
		} 
	}
	return (rm<=M); 
}


int main(){
	cin>>L>>N>>M;
	int mid,l = 0 , r= L;  // mid是模拟的最短距离的最大值，下面通过不停的二分，直到找到最符合的那个距离。 
	for(int i = 0; i < N ; ++i){
		cin>>a[i]; 	
	}
	while(l<=r){
		mid =  (l+r)/2;
		//删除石头的数量少于M，那么在mid距离之前的肯定都符合（即删除的只会更少，所以要往后走）
		if(check(mid)){ 
			l = mid + 1;
			ans = mid;
		}else{//删除石头的数量多余M，那么mid距离之后的肯定删除的会更多，所以往前走。
			r = mid - 1;
		}
		
	}
	cout<<ans;
	return 0;
}