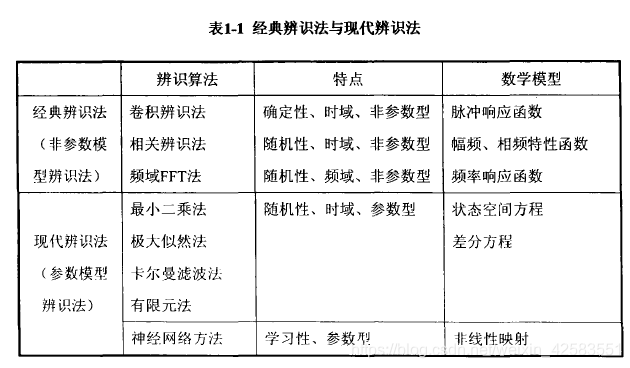
参数辨识三种方法
（1）解体测量方法：只能得到机械臂的惯性参数值，无法计算关节因素如关节弹性、摩擦的作用，必然引起较大的力矩偏差。
（2）CAD测量方法：无法对实际机器人关节中存在的复杂因素进行模拟
（3）整体辨识方法：给机器人的待辨识关节一个设计好的轨迹，机器人沿预设轨迹运动过程中，采集关节的驱动力矩及关节转角数据，将采样值带入到辨识模型中，通过算法求解出惯性参数的值。
一般都是采用整体辨识方法。
动力学参数辨识方案完整过程：
建立动力学模型，对动力学模型进行线化（辨识模型，得到用于动力学参数辨识的线性模型）、参数独立性分析及最小参数集、辨识轨迹优化、辨识算法构造、参数采集与处理、实验验证。（耿令波）
建模、激励轨迹设计、数据采样及处理、参数估计、模型验证（吴文祥）
看了多篇论文主要差异体现在辨识算法构造、参数采集与处理两点，考虑从这两方面着手选择方向深入挖掘。
- 机器人动力学参数辨识的目标
使机器人跟踪特定激励轨迹，更加精确
- 影响动力学建模精度的因素
实际情况中，存在众多因素影响动力学建模以及计算精度。有些影响因素无法建模或者无法精确建模，其次考虑因素越多，建立的动力学模型就会越复杂，
对控制硬件要求提高，增加控制成本，降低动力学计算的实时性。
1.结构参数
使用D-H方法描述串联机器人，相邻关节坐标系间的旋转变换矩阵为：
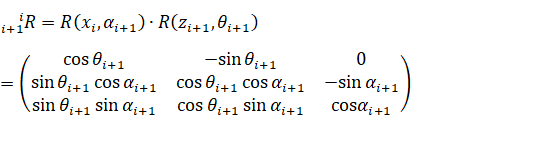
其中每个关节有4个参数（也叫运动学参数），分别为：a:相邻坐标系Z轴公垂线长度； α:相邻坐标系Z轴间的夹角; d:相邻坐标系x轴公垂线长度；
θ :相邻坐标系x轴间的夹角。
D-H方法不足：所有运动都是关于x和z的，无法表示关于y轴的运动。
2.惯性参数
作为已知值带入。受机器人加工、装配误差以及材料分布不均等的影响。
3.摩擦参数
一般采用线性摩擦模型：
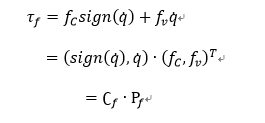
为摩擦力矩，˙
为库伦摩擦系数，
˙为符号函数，满足
。因此，完整的动力学参数模型可以写成向量的形式为：
Pdyn=(Ixx,Ixx,Ixy,Ixz,Iyy,Iyz,Izz,Hx,Hy,Hz,m,fc,fv,)T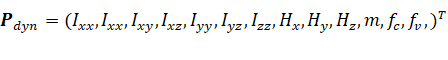
，其中Pdyn为动力学参数辨识的辨识对象，每个关节均包含10个机械臂惯性参数及2个关节摩擦参数
4.弹性
5.关节间的耦合
除了惯性参数及摩擦外，其他各因素不会产生附加的参数，因此动力学参数主要包括机械臂的惯性参数及摩擦参数。提高精度和降低成本两方面考虑，
采用动力学参数辨识的方式，在不改变动力学模型前提下，把其它因素的作用通过辨识过程包含进机械臂的惯性参数中，得到满足要求的综合参数。
三、数据采集：
首先得到最小参数集（相互独立的参数集合），从而保证辨识参数之间的独立性，使高精度的辨识结果成为可能。M.Gautier曾分别提出基于数值和符
号推导的两种最小参数集求解方法。
数据采集区别主要体现在力矩的采集上，关节运动参数、角速度、加速度由安装在电机上的编码器测得；力矩采集：力传感器直接测量和通过电机电流间接测量。
电流间接测量：将电机控制器的电流信号及轴向编码器的转角信号输出，通过电流测量值获得电机驱动力矩的大小。电机电流与驱动力矩关系：
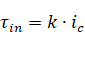
其中，τ为关节力矩，k为电机转矩常数，ic 为电机驱动电流。
四、动力学建模
机器人动力学模型体现机器人内在的力与运动的关系。基于模型的控制器可以给出机器人进行目标运动所需要的力矩值（力矩对应机器人理想的
转角和角速度及加速度），因此能够实现对轨迹的精确跟踪。
动力学模型包含3类参数：运动学参数、惯性参数和摩擦参数。运动学参数包含连杆长度、扭角和偏置，是已知的。惯性参数包含连杆质量、
一节质量矩和惯性矩。摩擦参数
目前用于工业机器人动力学建模的方法有很多,比如牛顿欧拉方法、拉格朗日方法、高斯方法、凯恩方法，算子代数法等。对于确定的工业机器人系统，
不同的建模方法得到的动力学模型是等价的。可以表示为：
,
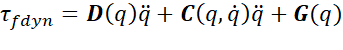其中，q为关节角向量 Dq为惯性项（正定对称惯性矩阵），Cq,q 为科氏力及离心力项，G(q)为重力项，每一项都是机器人惯性参数与关节
运动参数的函数。机器人的10个惯性参数用向量形式可表示为
Piner=(Ixx,Ixx,Ixy,Ixz,Iyy,Iyz,Izz,Hx,Hy,Hz,m)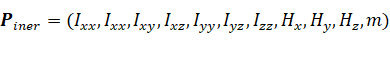
,
其中，参数Ixx~Izz是机器人惯性项量I中的6个参数， Hx,Hy,Hz是H=m×
=m(rcx,rcy,rcz)的3个分量（为质心向量）
（1）牛顿欧拉方法建模
牛顿欧拉方法采用递推形式，易于编程实现。基于力平衡方程和力矩平衡方程两个基本方程：
表示作用于机械臂质心处的合力，
表示机械臂质心的线加速度，
表示作用于机械臂质心处的合力矩，
表示相对机械臂质心表示的
机械臂惯量矩阵，α表示机械臂角的加速度，ω表示机械臂的角速度。牛顿欧拉动力学建模方法包括两部分，正向运动学递推及反向动力学递推：
五、辨识（激励）轨迹选择
（1）J.Swevers提出的傅里叶级数型的辨识轨迹：
q=q0+i=1NaisinφfikTs+i=1N(bicosφfikTs),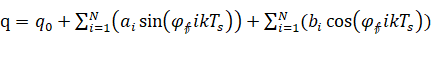
其中ai，bi为轨迹的系数，φf为轨迹的基频，K为采样个数，Ts为采样周期。优点：可以通过对转角信号进行离散傅里叶变换直接求出角速度、
加速度的表达式，无需对关节转角信号进行微分，减小了由于微分引起的噪声，使得辨识结果对于干扰的抑制能力加强。
缺点：傅里叶级数不满足速度、加速度的边界条件。因而，在实验的开始和结束阶段，存在速度和加速度的涂遍，导致机器人颤振，
难以准确跟踪激励轨迹，进而降低参数辨识的精度。
（2） 吴文祥 基于傅里叶技术改进
添加边界条件，并未增加优化问题的自由度。优点：更准确跟踪激励轨迹，为采用解析法计算角速度、角加速度信号奠定基础。
(3).激励轨迹优化
为提高辨识精度，需选取合适的指标函数优化激励轨迹．Ｓｗｅｖｅｒｓ等采用ｄ最优准则优化激励轨迹．
Ａｎｔｏｎｅｌｌｉ通过最小化观测矩阵的条件数，同时最大化观测矩阵的最小奇异值来优化激励轨迹．Ｋｏｓｔｉｃ等采用观测矩阵的条件数作为优化准则
六、辨识算法选择：
可用于动力学参数辨识的算法：神经网络辨识，遗传算法辨识，最大似然估计辨识、卡尔曼滤波算法辨识、最小二乘法辨识等。
（1）最经典的最小二乘法（见耿令波，李保丰）
数据处理量大，方法构造简单，参数设置无需任何经验，无需将动力学转换为状态方程的形式。
（2）神经网络算法
处理线性问题时效率低
（3）最大似然估计（见吴文祥）
测量噪声会影响参数估计的精度
（4）粒子群算法（见傅霞君）
对机械臂进行离线识别。该方法简单有效，无需附加传感器。将待识别参数分为线性和非线性部分，
并对其分别采用线性最小二乘法和粒子群算法进行结算，从而得到机械臂的动力学参数和摩擦系数。
连接组合体的辨识方法;通过将关节进行锁定，每次都相当于辨识最末关节的参数，参数数目大大减少；各次辨识相互独立，
精度相当，不会引起大的误差累积：另外，由于每次都相当于辨识最末关节，得到的是连接组合体参数的独立值，
每个关节的最小参数集参数可由连接组合体的参数表示，当负载改变时，连接组合体的参数是可求的，因此辨识结果不受负载变化影响。
看论文模仿一篇的粗糙思路
建立动力学模型， 牛顿欧拉方法建模
模型进行线化（辨识模型）、
最小参数集、 惯性力矩： 瞬时角速度、线速度、角加速度
辨识轨迹优 傅里叶级数轨迹
轨迹优化 看的论文大都是针对某具体的机械臂进行优化，
辨识算法构造、 最小二乘法+？？？神经网络
+粒子群算法（已知采用的多）
参数采集与处理、
实验验证 matlab