最近数学建模实验学习到了非线性规划部分,这一部分的内容是最优化问题结合实际生活最重要的一部分。对于数学规划问题,我们常常使用Lingo软件来分析,当然我们还可以使用Matlab的函数进行分析。
非线性规划
- 无约束非线性规划


对于无约束非线性规划问题,在Matlab中我们常常使用函数 fminsearch 和 fminunc 来实现。(具体的语法本文就不再介绍)
2. 约束非线性规划
约束非线性规划(constrained nonlinear programming )问题是在实际生活中经常用到的一类数学规划问题,广泛存在于经济、交通、能源、管理等等技术领域。

对于解决这类数学规划问题,我们可以使用Matlab软件的 fmincon 函数。

[x,fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
x的返回值是决策向量x的取值,fval的返回值是目标函数f(x)的取值
fun是用M文件定义的函数f(x),代表了(非)线性目标函数
x0是x的初始值
A, b, Aeq, beq定义了线性约束 ,如果没有线性约束,则A=[], b=[], Aeq=[], beq=[]
lb 和 ub是变量x的下界和上界,如果下界和上界没有约束,则lb=[],ub=[],也可以写成lb的各分量都为 -inf, ub的各分量都为inf
nonlcon是用M文件定义的非线性向量函数约束
options定义了优化参数,不填写表示使用Matlab默认的参数设置
下面,我们就举一道例题来看看如何应用:
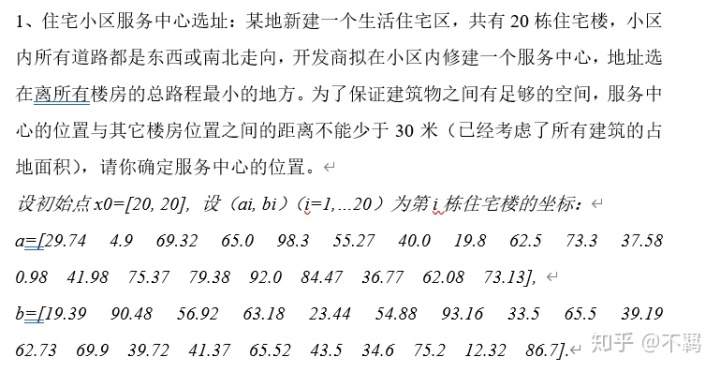
一、由题目可以得:
1、所有的建筑物可被看作是质点,服务中心到其他楼房的距离小于30米;
2、小区所有道路的走向为南北或东西走向。
二、问题分析:
本题是一道最优化问题,我们需要求解各楼房到所有楼房总距离的最小值。将图像转移到 x、y轴平面,即求已知各点到目标点的距离并求出目标点的位置。于是,需要先求最小坐标——决策变量寻求的点。本题中使用计算机在可行域内迭代求解位置。
三、决策变量及目标函数:
1、平面内有20个点,代表20栋楼的坐标用(
2、决策变量:设服务中心的坐标(x, y)。
3、约束条件:
不等式的约束条件:
自然约束条件:x, y ≥ 0;
4、目标函数:
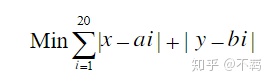
四、实验代码
1、建立目标函数程序:target1.m
function2、建立约束条件函数:func2.m
function3、Matlab最优解程序:task1.m
clear运行结果:

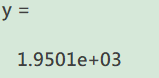
综上所述:服务中心的坐标位置为:(1.2812, 9.8980),总路程最小值为:
本人也只是刚接触非线性规划内容,以上分析过程和代码大部分由本人编写稍有不足之处,望各位能够指正。