系列文章:
- 双目视觉(一)双目视觉系统
- 双目视觉(二)双目匹配的困难和评判标准
- 双目视觉(三)立体匹配算法
- 双目视觉(四)匹配代价
- 双目视觉(五)立体匹配算法之动态规划全局匹配
- 双目视觉(六)U-V视差
- 【项目实战】利用U-V视差进行地面检测
- 【项目实践】U-V视差路面检测之动态规划
匹配代价,说白了就是衡量像素之间的相似程度,当代价越大,左右图像相应的像素点越不相似。在立体匹配中,常用的匹配代价:AD, SSD, SAD,Census,, NCC,BT,MI,LOG等
1. AD
AD变换反映像素点的灰度变化,在纹理丰富区域具有良好的匹配效果,是一种简单、易实现的代价衡量的方法。但是,基于单个像素点计算的匹配代价往往会受到图像噪声、光照不均等的影响,相似度可靠性不高。
- 颜色差异的绝对值:
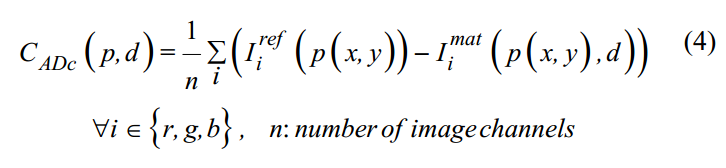
- 梯度差异的绝对值:
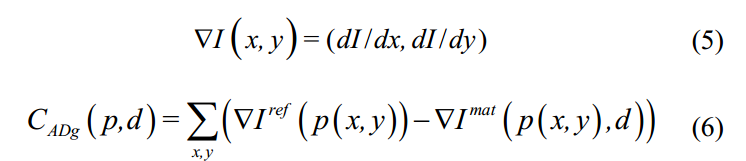
- 参考论文:
- a local adaptive approach for dense stereo matching in architectural scene reconstruction(2013)
2.SAD
SAD(sum of absolute difference)为像素领域内对应位置灰度差的绝对值之和,可以很容易的嵌入到FPGA中,实现实时,但是两幅图像的灰度值易受光照影响。
- 公式:
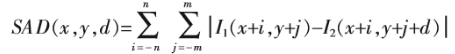
3.SSD
SSD(Sum of Squared Difference)为像素差的平方和,相对于SAD具有更高的复杂度,因为具有乘法操作。同时,SAD更加鲁棒,SSD易受噪声影响。
- 公式:
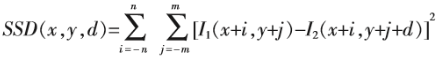
注:SAD和SSD都直接利用图像的灰度信息值,所以对光照的变化十分敏感,其次,采用的领域窗口为矩形,对于旋转和缩放比较敏感,当发生较大尺度的旋转和尺度缩放时,窗口内的点将发生较大变换。
4.NCC
NCC :归一化互相关系数(归一化:消除对光照敏感的问题),对不同的光照强度更加鲁棒,但是复杂程度更高,仍然采用的矩形窗口,对旋转和尺度变换敏感。
- 公式:
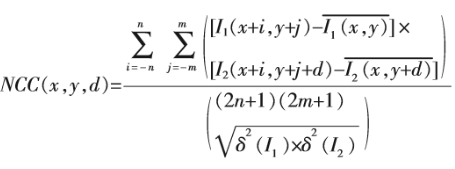
其中:
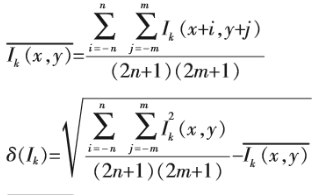
注:NCC适合小的窗口,SAD,SSD适合大的窗口
5. census变换
在1994年,Zabih和Woodfill 提出了Census transform,后来被广泛用于计算机视觉领域中的匹配代价计算。Census变换是在图像区域定义一个矩形窗口,用这个矩形窗口遍历整幅图像。选取中心像素作为参考像素,将矩形窗口中每个像素的灰度值与参考像素的灰度值进行比较,灰度值小于或等于参考值的像素标记为0,大于参考值的像素标记为1,最后再将它们按位连接,得到变换后的结果,变换后的结果是由0和1组成的二进制码流。如下图所示。

Census变换的匹配代价计算方法是计算左右影像对应的两个像素的Census变换值的汉明(Hamming)距离。

- 优点:
Census变换对图像的明暗变化不敏感,能够容忍一定的噪声,因为比较的是相对灰度关系,所以即使左右影像亮度不一致,也能得到较好的匹配效果。而且,相比互信息具有并行度高的优点,Census变换值是局部窗口运算,每个像素可以独立运算,这个特性让其可以很好的设计多线程并行计算模型,无论是CPU并行还是GPU并行都能达到非常高的并行效率。
- 缺点:
census变换在双目匹配中对于弱纹理区域和重复场景的匹配效果不好。例如:灰度完全不同的两个邻域窗口,Census变换得到的代价相同。

- 参考文献:
- ZABIH R, WOODFILL J. Non-parametric local transforms for computing visual correspondence[M]. 1994: 151-158
- a local adaptive approach for dense stereo matching in architectural scene reconstruction(2013)
6.BT
BT方法主要解决图像深度不连续的问题

- 参考:
7.MI
信息量
信息量是指信息多少的量度,举个简单的例子,以下两个句子,哪一个句子的信息量更大呢?
- 我今天没中彩票
- 我今天中彩票了
从文本上来看,这两句话的字数一致,描述的事件也基本一致,但是显然第二句话的信息量要比第一句大得多,原因也很简单,因为中彩票的概率要比不中彩票低得多。一个信息传递的事件发生的概率越低,它的信息量越大。用一个函数来描述信息量需要满足如下条件:

满足上述条件的函数是对数函数,因此我们用对数函数来量化一个事件的信息量:
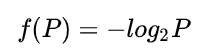

信息熵
在信息论中,熵是接收的每条消息中包含的信息的平均量【用期望表示】,熵的单位通常为比特,但也用Sh、nat、Hart计量,取决于定义用到对数的底。
连续的:
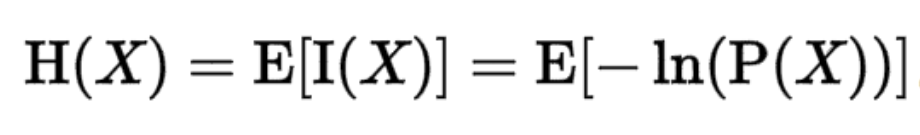
离散的:
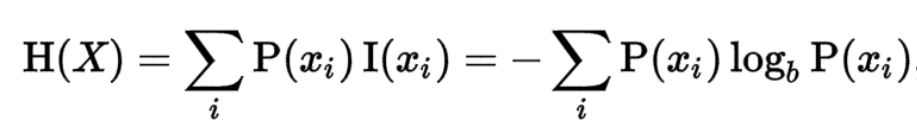
互信息
两个随机变量的互信息(Mutual Information,简称MI)是两个变量相互依赖性的量度:单独考虑两个变量、综合考虑两个变量,如果这两种情况导致的结果差别很大,则他们关系不浅啊。
互信息与熵的关系:在给定Y知识的条件下,X的不确定度的缩减量
![]()
- H(Y):随机变量Y不确定度的量度。
- H(Y|X):随机变量X没有涉及到的随机比变量Y的部分的不确定度的量度,也就是“在X已知之后Y的剩余不确定度的量”。
- H(Y)-H(Y|X):Y的不确定度,减去在 X 已知之后 Y 的剩余不确定度的量,等价于:移除知道 X 后 Y 的不确定度的量。
公式推导:
参考:
- 关于信息论中熵、相对熵、条件熵、互信息、典型集的一些思考
- 机器学习笔记十:各种熵总结
- https://www.jiqizhixin.com/graph/technologies/7afc5fc3-a61c-4238-b496-9c39392a91fe
- https://blog.csdn.net/xierhacker/article/details/53463567
- https://www.zhihu.com/question/41252833
- https://www.jianshu.com/p/43318a3dc715
8.组合代价:AD-Census
