目录
插入类
插入排序
时间复杂度: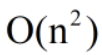
空间复杂度: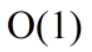
排序的稳定性:稳定
适用范围:大部分已经有序的序列
希尔排序
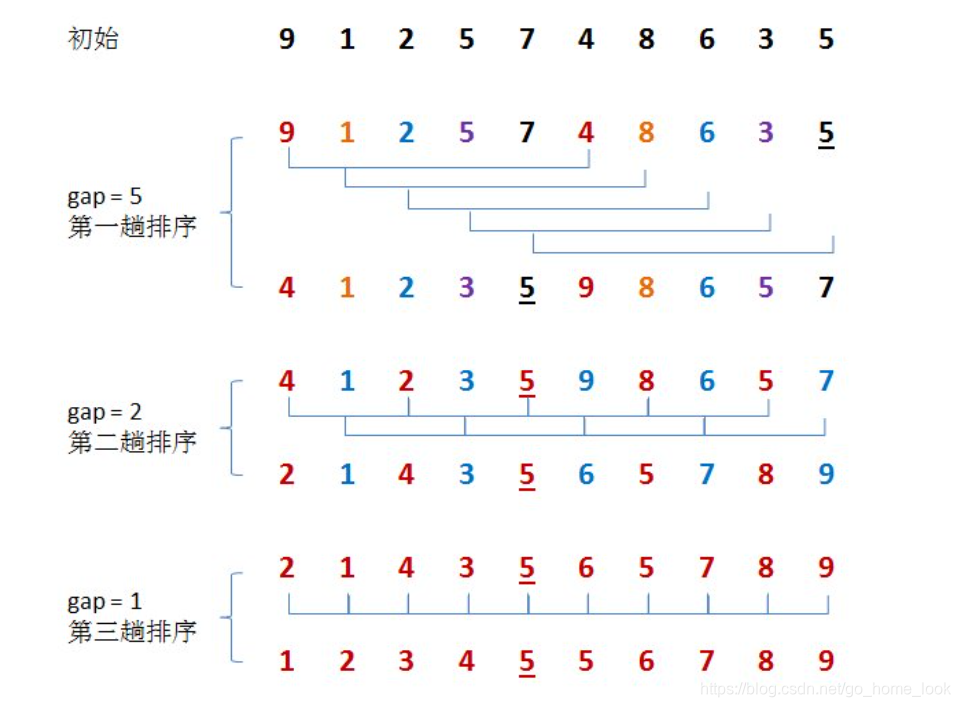
时间复杂度:![]()
空间复杂度: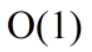
排序的稳定性:不稳定
交换类
冒泡排序
目录
冒泡排序的思想是比较两两相邻的关键字,如果反序则进行交换,直到没有反序的为止。原理理解查看博客
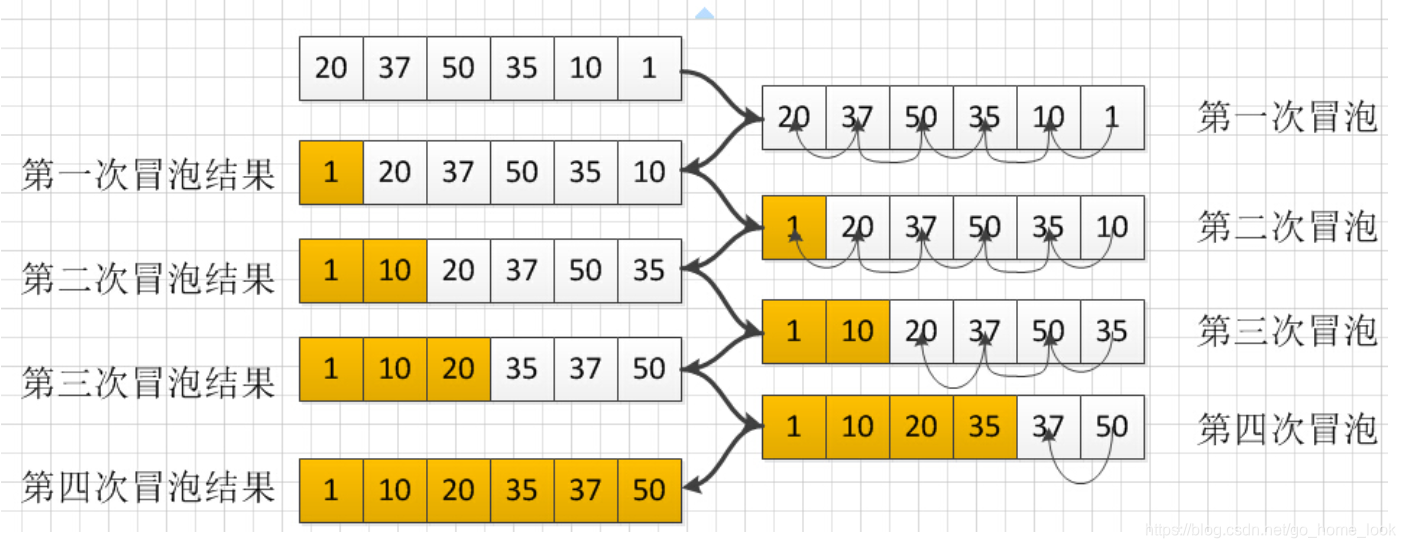
时间复杂度: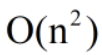
空间复杂度: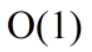
排序的稳定性:稳定
#include <stdio.h>
int main()
{
int i=0;
int j=0;
int max=0;
int length=5;
int a[5]={7,9,1,5,2};
/*冒排序思想:从最前面开始 相邻的两两比较选出最大的 放在最后面 */
printf("original sort:");
for(i=0;i<=length-1;i++)
{
printf("%d ",a[i]);
}
printf("\n");
for(i=0;i<=length-1;i++)
{
/*这里每次选出一个最大的来放在最后面 j 的位置就要被占用1个,所以要减 i */
for(j=0;j<length-1-i;j++)
{
if(a[j]>a[j+1])
{
max=a[j];
a[j]=a[j+1];
a[j+1]=max;
}
}
}
printf("bubble sort:");
for(i=0;i<=length-1;i++)
{
printf("%d ",a[i]);
}
printf("\n");
return 0;
}
输出结果:
original sort:7 9 1 5 2
selection sort:1 2 5 7 9快速排序
看了老哥的这篇文章,再加上自己的总结就是:“坑左右填”坑在左边出现时就从右边的指针往前找一个小于基准值的放到坑内,“坑右左填”当坑出现在右边时就从左边的指针往后找一个大于基准值的放到坑内,最后两个指针指向同一个地方了就把基准值放进去
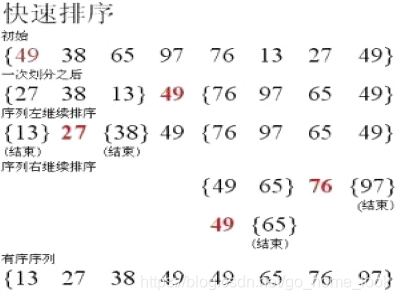
时间复杂度:![]()
空间复杂度:![]()
排序的稳定性:不稳定(如果两个相同的数一定是第一个被放入最小的位置,下一次才是第二个,所以位置发生改变)
如果在待排序的数据表已经为有序时,花费时间反而变多
选择类
选择排序
第一轮选出一个最小的元素放在0的位置,之后这个元素的位置就不需要再动了,第二轮选出剩余元素中最小的一个放在1的位置,如此循环,每轮从剩余的元素中选出最小的,原理理解查看博客
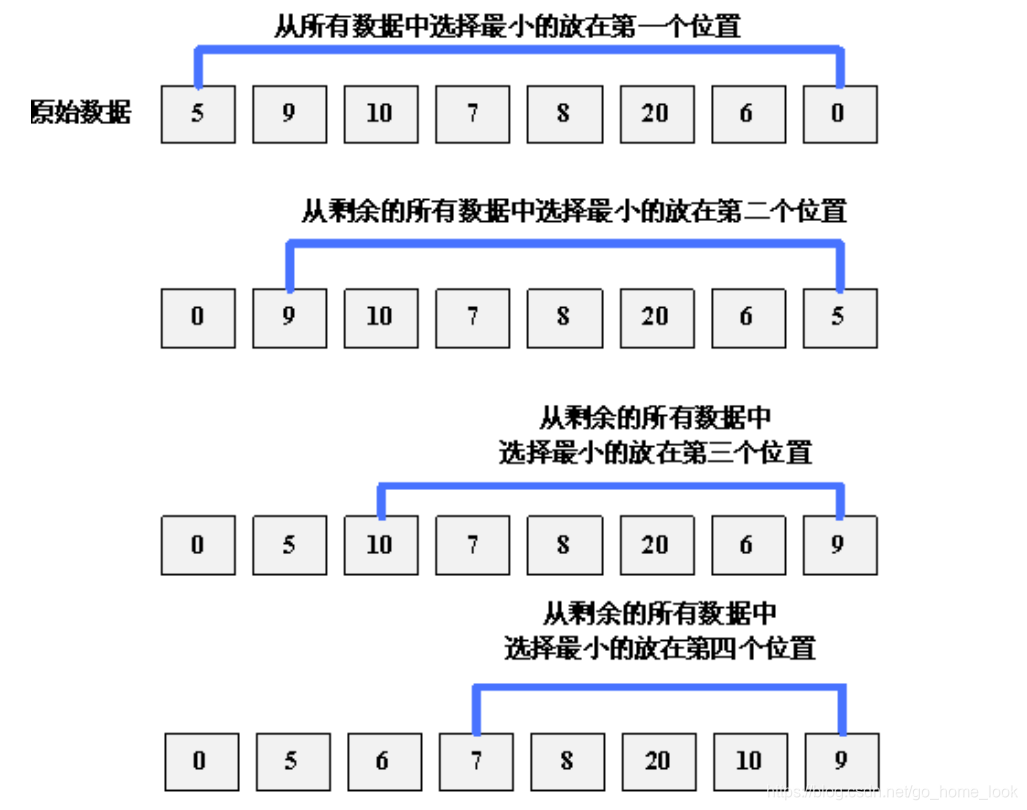
时间复杂度: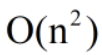
空间复杂度: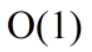
排序的稳定性:不稳定
#include <stdio.h>
int main()
{
int i=0;
int j=0;
int min=0;
int length=5;
int a[5]={7,9,1,5,2};
/*选择排序思想:从n-i各元素中选出最小的 从最前面开始放
* */
printf("original sort:");
for(i=0;i<length;i++)
{
printf("%d ",a[i]);
}
printf("\n");
for(i=0;i<=length-1;i++)
{
/*每次都从剩下的 a[j]中选出最小的,放入最前面的 a[i] */
for(j=i;j<length;j++)
{
if(a[j]<a[i])
{
min=a[j];
a[j]=a[i];
a[i]=min;
}
}
}
printf("selection sort:");
for(i=0;i<length;i++)
{
printf("%d ",a[i]);
}
printf("\n");
return 0;
}
输出结果:
original sort:7 9 1 5 2
selection sort:1 2 5 7 9 堆排序
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
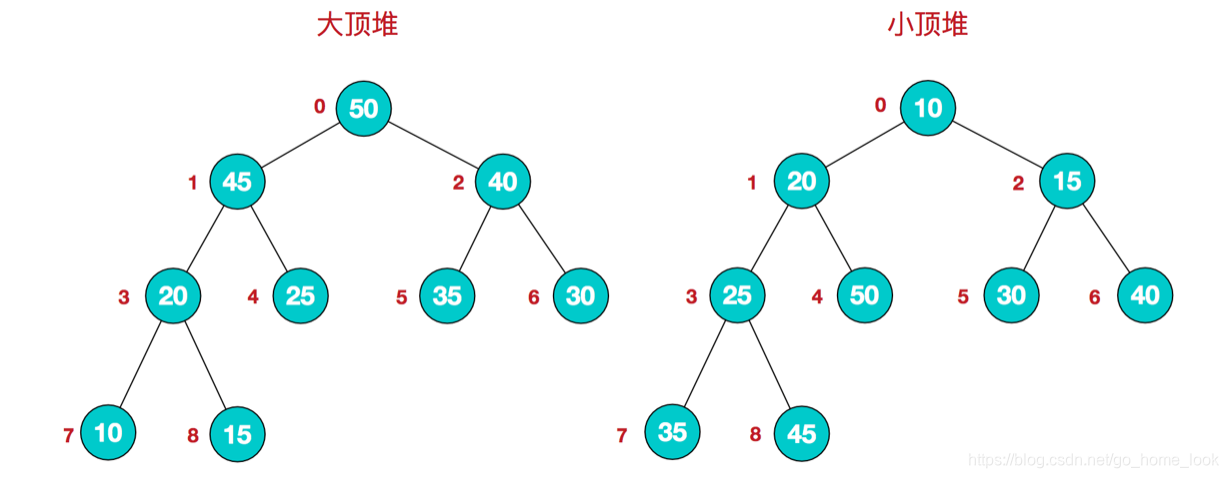
时间复杂度:![]()
空间复杂度:
排序的稳定性:不稳定
归并类
2-路归并排序
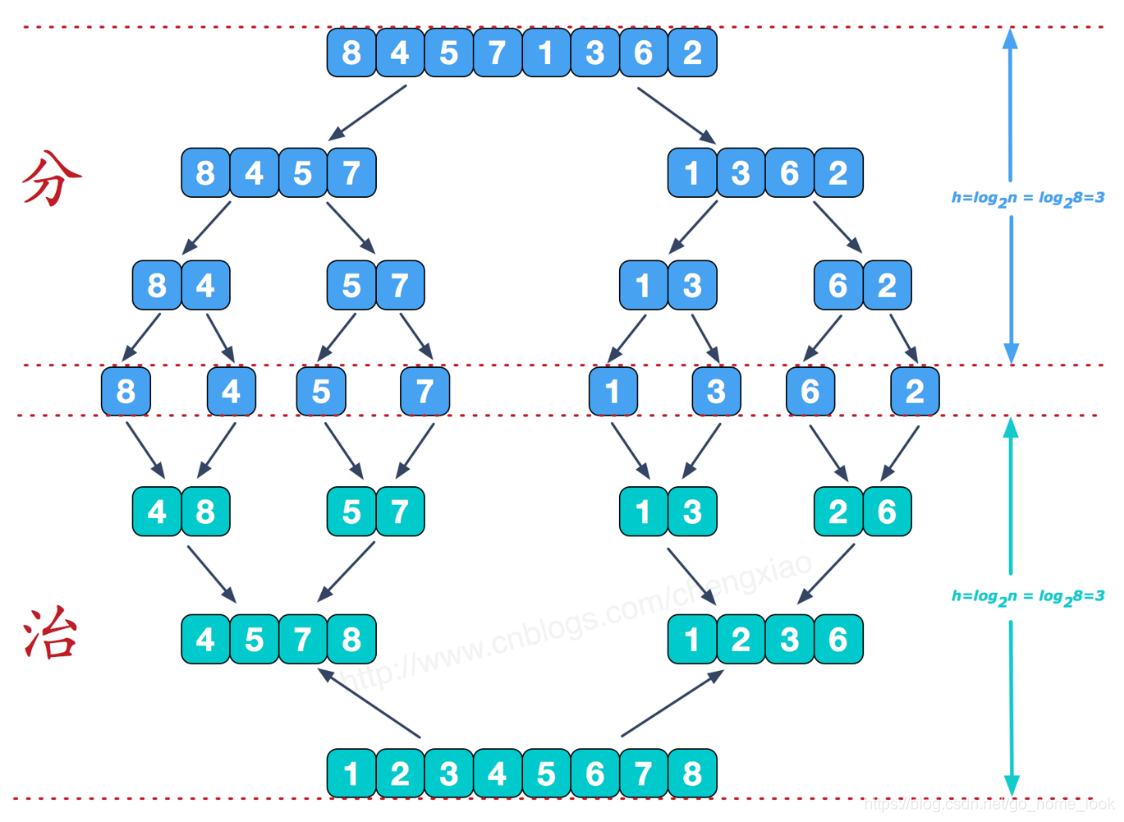
https://www.cnblogs.com/chengxiao/p/6194356.html
时间复杂度:![]()
空间复杂度:![]()
排序的稳定性:稳定
分配类
桶排序

https://blog.csdn.net/qq_37186247/article/details/100834916
时间复杂度:![]()
空间复杂度:![]()
排序的稳定性:稳定
基数排序
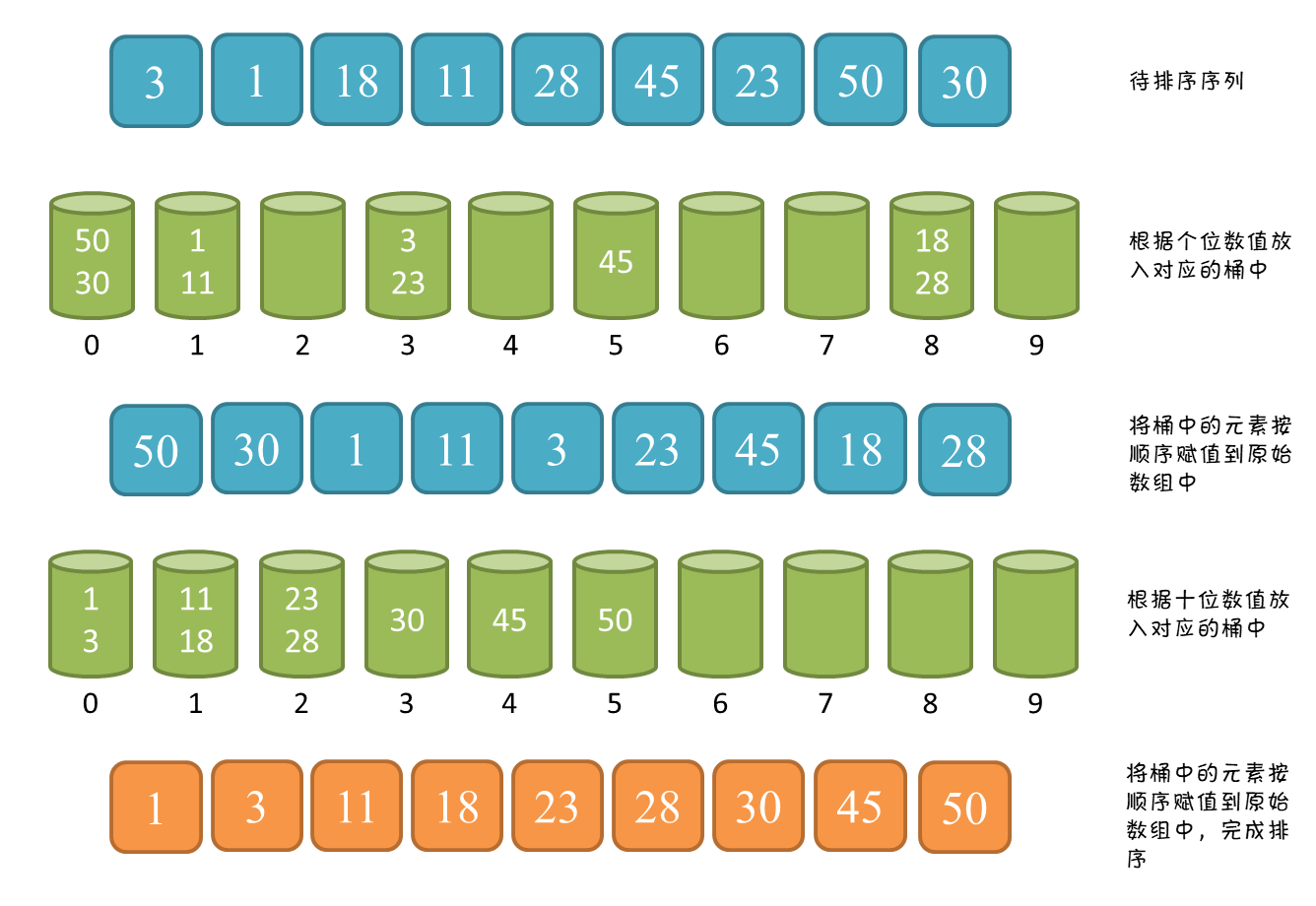
时间复杂度:![]()
空间复杂度:![]()
排序的稳定性:稳定
红黑树
https://www.cnblogs.com/lizhangyong/p/8060110.html
时间复杂度: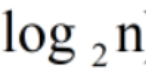
序列的稳定性
当待排序列中存在两个及两个以上关键字相等的记录时,假设待排序列中有两个相等的关键字K1=K2,若在排序前K1位于序列中的i位置K2位于序列中的j位置且i<j 即K1在前面K2在后面,排序完成后若K1所在位置i任然小于K2所在位置j就说序列稳定,反之若经过排序K2位于K1前面原来先后顺序发生改变就说序列不稳定
时间与空间复杂度