对神经元和spike信号进行建模

我们的目标是建立一个简化的符合真实生物学意义的神经元模型—其中包括一个胞体，一个收集其他神经元输入的树突，以及一个将胞体内或附近产生的动作电位传递给其他神经元的轴突。
我们需要将这种生物学上的联结用电路图的形式进行处理。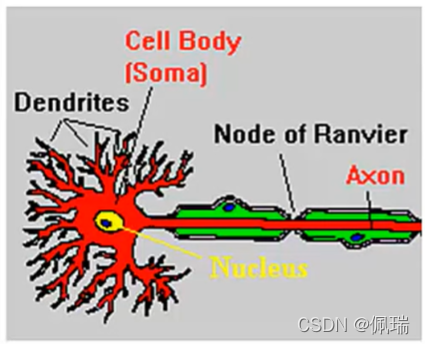

RC电路（一）— 被动细胞膜

细胞膜是脂质双层的，而磷脂和脂肪都是非常好的绝缘体，其中嵌入的离子通道会选择性的让离子通过，从而出现电流交换，但是在被动细胞膜的前提下我们不考虑离子通道，只考虑穿透细胞膜本身的微小电流。

• 细胞膜本身可以被看作储存电流的电容C
• 细胞膜本身具有一定的电阻R
  
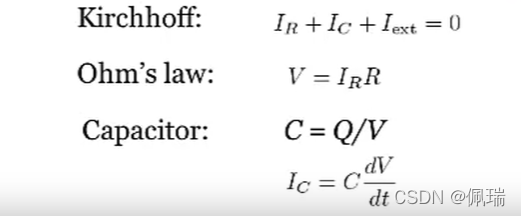
• 应用上述物理公式进行变换，得到有关RC电路膜电势V的函数：$C\frac{dv}{dt}=-\frac{V}{R}+I_{ext}$ ,这里的$I_{ext}$为外部输入电流。

RC电路（二）— 离子通道

膜内外离子浓度差

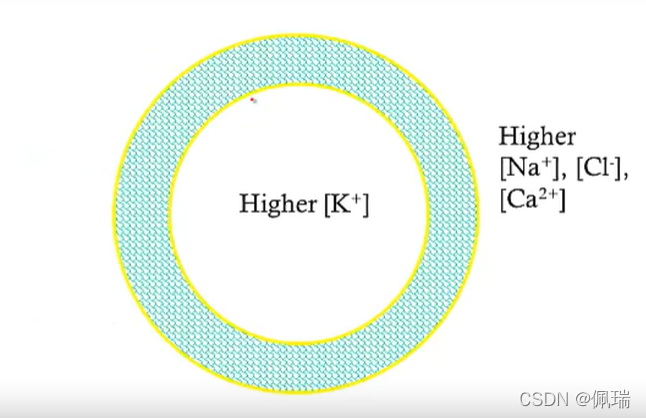
引入离子通道之前，我们需要先处理细胞膜内外离子的浓度差，即细胞膜的离子和电势流动遵循一定的梯度，并会最终达到平衡。

• 根据细胞膜的这种电势梯度我们引入静息电位$V_{rest}$
• 得到有关RC电路膜电势V的函数：
  $C\frac{dv}{dt}=-\frac{(V-V_{rest})}{R}+I_{ext}$ ,这里的$I_{ext}$为外部输入电流。
• 对于上述微分方程我们进行数学变换得到：
  $\tau \frac{dv}{dt}=-V+V_{\infty }$,此时$\tau =R\times C,V_{\infty }=$study state
  
• $\tau$是时间常数，$V_{\infty }$是学习状态，在初始阶段V=0，随后随时间以及外部电流的输入，V不断呈指数增大直到达到$V_{\infty }$后不再继续增长，之后随电流输入的停止电压V也随之回落到0。

电压门控离子通道

嵌入在细胞膜中的离子通道有着各式各样的特征，但是在RC电路里，我们主要聚焦于电压门控离子通道的建模。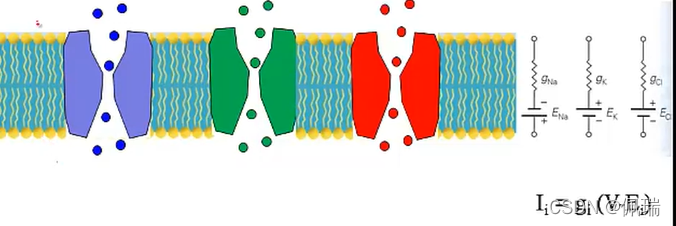

去极化时主要是Na离子通道开放，而超极化时则主要是K离子通道开放，并且离子通道有多种状态，每一种状态对应的电阻R不同，因此在电路图中用可变电导g来表示，并用E表示每一离子通道的平衡电势。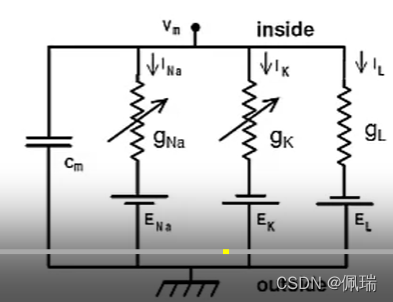

• K离子通道门控开关依赖4个相互独立的激活组件n，Na离子通道门控开关依赖3个互相独立的激活组件m以及一个失活组件h：
  $P_k$ ~ $n^4$,$P_k$是k离子通道的开放概率,n为组件的开放概率
  $P_{Na}$ ~ $m^{3}h$,同理
• 在这里定义状态转换概率${\alpha }_n(V)=close\to opening,{\beta }_n(V)=opening\to close$
• 不同状态之间转换的速率可以用微分方程表示：
  $\frac{dn}{dt}={\alpha }_n(V)(1-n)-{\beta }_n(V)n$
  Na离子通道同理。
• 对于上述方程进行数学转换可以得到：
• ${\tau }_n(V)\frac{dn}{dt}=n\infty (V)-n$，其中$\tau =\frac{1}{{\alpha }_n(V)+{\beta }_n(V)}$描述打开通道的比例如何随时间变化,$n_{\infty }=\frac{{\alpha }_n(V)}{{\alpha }_n(V)+{\beta }_n(V)}$表示多久通道才会打开，Na离子通道同理。
• 最后我们得到有关RC电路膜电势V的函数：
  $C_m\frac{dv}{dt}=-\sum _i{g}_i(v-E_i)+I_e$, $C_m\frac{dv}{dt}$是通过细胞膜的电流，$\sum _i{g}_i(v-E_i)$是离子通道电流,$I_e$是非特异性离子运动电流和外部输入电流的总和。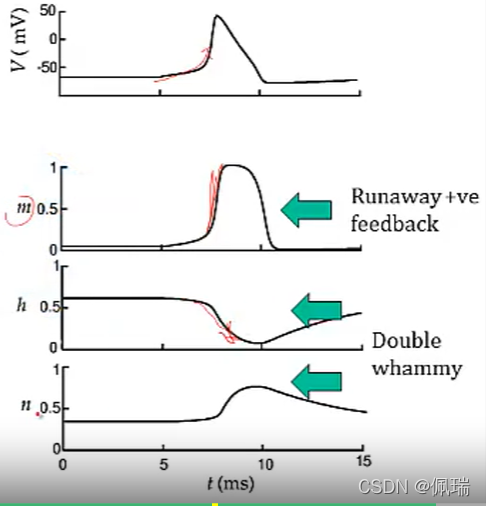
  
  从上图可以看出我们建立的模型已经可以对于spike响应进行简单仿真了。这个模型也被叫做Hodgkin Huxley Model，有关模型的更多应用可以查看这一篇文章。
  神经元内信号传递的计算模型-HH模型
  欢迎大家关注公众号奇趣多多一起交流！