这一篇我们要说说关于
解的概念和关系
介绍几个概念
在此之前,先说明一下“背景”:
我们前面的约束条件方程组,看成一个(n×m)的矩阵,要求n>m
几个没必要详细说的名词
1.最优解:满足目标方程的解
2.基:设上面说的矩阵的秩为 m,B为m×m的满秩矩阵(|B|不等于0),则B就是基
3.基向量:基B的每一列看成是一个基向量Pi
4.基变量:每个基向量对应一个基变量,其实就是基B对应的未知数吧
5.非基变量:除了基变量以外的变量都是非基变量
1.基解:对一个基B,令非基变量 = 0,解出来基变量的值,和非基变量合在一起就是基解
X = (X1,X2,X3,...Xn)T T表示是列 (Xi 为非基变量就等于0,为基变量就是解出来的值)
2.可行解:根据约束方程画出来的可行域内的解都是可行解
3.基可行解:所有基解中(因为不只一个满秩矩阵) 满足所有Xi大于0的解就是基可行解,
对应在可行域(有界为凸集)的顶点(不是一一对应)对凸集而言,顶点有限个
(凸集的证明:集合中任意两点的连线任然属于这个集合)
4.可行基:对应基可行解的基B
5.最优解:如果存在最优解,那一定是一个基可行解是最优解(顶点上的)
6.基最优解:最优解唯一的时候,最优解就是基最优解
最优解不唯一,最优解不一定是基最优解
他们的关系:箭头指向为范围扩大
例如,是基可行解一定是基解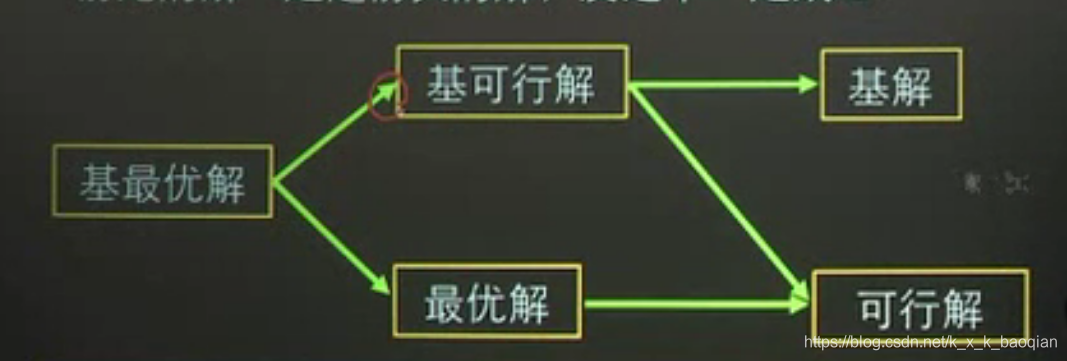
版权声明:本文为k_x_k_baoqian原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。