稀疏保持投影
参考论文:sparsity preserving projections with applications to face recognition
作者:Lishan Qiao,Songcan Chen,Xiaoyang Tan 2010
一、主要思想
线性降维方法:PCAf关注于全局,但对于非线性的数据结构,PCA的结果并不好
流行学习:Isomap,LLE,LE来处理非线性流行结构数据,但他们没有继承传统PCA的优点。LPP是LE的线性近似和NPE和LEA是LLE的线性近似,但是怎么确定邻居的尺寸还是难题。
SPP模型中,基于改进的稀疏表示来构造邻接权重矩阵。
二、算法步骤
2.1 稀疏表示权重
给定数据{x 1 , x 2 , . . . , x n x_1,x_2,...,x_nx1,x2,...,xn},其中x i ∈ R m x_i∈R^mxi∈Rm
m i n s i ∣ ∣ s i ∣ ∣ 1 s . t . x i = X s i , 1 = 1 T s i min_{s_i}||s_i||_1\\s.t.x_i=Xs_i,1=1^Ts_iminsi∣∣si∣∣1s.t.xi=Xsi,1=1Tsi (12)
其中s i s_isi={s i 1 , . . . , s i , i − 1 , 0 , s i , i + 1 , . . . , s i n s_{i1,...,s_{i,i-1},0,s_{i,i+1},...,s_{in}}si1,...,si,i−1,0,si,i+1,...,sin}T(第i ii个元素为0,意味着把x i x_ixi移出X XX),s i j , j s_{ij},jsij,j≠i ii,表示每一个x j x_jxj对重构x i x_ixi的贡献,1 11是全1列向量。
最后S = S=S={s 1 ′ , s 2 ′ , . . . s n ′ s'_1,s'_2,...s'_ns1′,s2′,...sn′},s i ′ s'_isi′为上述得到的优化的s i s_isi。
根据论文《Robust face recognition via sparse representation》,有两种解决上述MSR问题的方法:
第一种: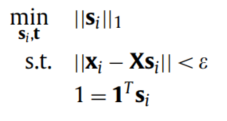 (15)
(15)
其中ϵ \epsilonϵ为error tolerance
第二种:
用[ X , I ] [X,I][X,I]代替X XX,其中I II为m mm维单位矩阵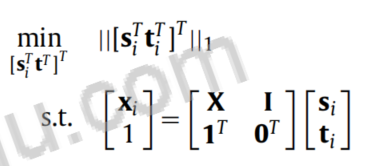 (16)
(16)
其中t i t_iti是m mm维向量。
2.2 保持稀疏重构权重
通过上述计算,我们可以得到稀疏权重矩阵S SS,类似于LLE和NPE,有以下目标函数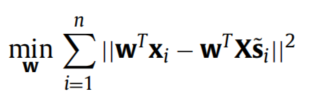
从而:
添加约束w ′ X X ′ w = 1 w'XX'w=1w′XX′w=1,得到: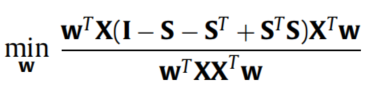
令S β = S + S ′ − S ′ S S_{\beta}=S+S'-S'SSβ=S+S′−S′S得到: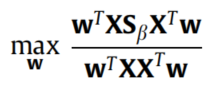
类似于PCA,NPE,最优的w ww就是下面广义特征值问题的前d dd个最大的特征向量: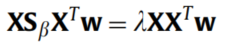 (22)
(22)
基于上述讨论,总结得到SPP的算法如下:
注:对于许多高维数据,矩阵X X ′ XX'XX′通常是奇异的,因为训练样本数比特征维数要小的多。为了解决这个问题,训练样本首先被投影到PCA子空间通过对应的特征向量W p c a = [ w 1 , w 2 , . . . , w d ’ ] W_{pca}=[w_1,w_2,...,w_{d’}]Wpca=[w1,w2,...,wd’],然后矩阵X X ′ XX'XX′近似为: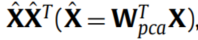
显然这是非奇异的!