今天主要想说的是,分形中的差分盒子维数的原理,基于分形的基础概念就不在这里说啦.
分形维数可以用于定量描述图像表面的空间复杂程度,能够定量的表现图像的纹理特征. 采用不同的维数进行纹理特征描述时,精度有所区别,我们今天主要来说一下比较简单的盒子维.
1.差分盒子维数
Gangepain 和 Roques-Carms 在1986年提出基于盒计数(Box-counting)的分形维数,通过计算覆盖图像表面的最小盒子数来度量.
说得详细一点:将一幅大小为
注:一般灰度图像的灰度级为 L = 256.若在第
覆盖整个盒子的数为
由此可求分形维数D为:
式中:
通过改变网格
2.实验
我们先来看一下,将灰度图像看作三维物体的表面灰度集是怎么样呢?
① 实现灰度图像的表面灰度集,采用matlab程序,如下:
function Show_GraySurface(filename)
% 把一幅图像看成三维空间的曲面,
% 像素的位置(x,y)构成xoy坐标面,
% 像素的灰度值看成z轴的值由此构成灰度曲面
picture_dir = 'D:Matlabworktest';
I = imread([picture_dir,filename]);
if (length(size(I)) > 2)
I = rgb2gray(I);
end
M = size(I,1);
Temp = diag(1:256)*ones(256,256);
x = reshape(Temp.',1,M*M);
y = reshape(Temp,1,M*M);
z = reshape(I,1,M*M);
tri = delaunay(x,y);
trisurf(tri,x,y,z);
shading interp
view(3);grid on;colorbar
end附加:python程序
import cv2
import numpy as np
import matplotlib.pyplot as plt
def surface(img):
X = np.arange(0, 363, 1) # cols of the image
Y = np.arange(0, 480, 1) # rows of the image
X,Y = np.meshgrid(X,Y) # extending points
Z = np.array(img) #2 dimension
fig, ax = plt.subplots(subplot_kw = {"projection": "3d"})
surf = ax.plot_surface(X, Y, Z, cmap = "rainbow", linewidth = 0, antialiased = False)
ax.contour(X, Y, Z, zdir = 'z', offset = 75, cmap = plt.get_cmap('rainbow')) # projection
fig.colorbar(surf) # colorbar
plt.show()
if __name__ == "__main__":
img = cv2.imread("3.jpg", 0)
surface(img)
注:matlab程序中,图像大小256 x 256.效果如下:
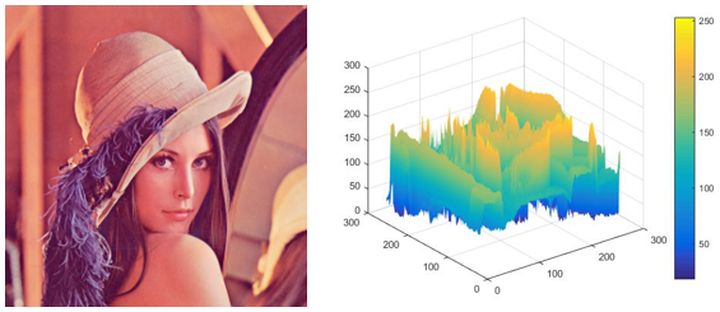
② 计算差分盒维数,采用Python程序.
★ 主程序文件:main.py
import cv2
from DBC import Fractal
src = cv2.imread("D5.jpg", cv2.IMREAD_UNCHANGED)
# create an object
obj = Fractal()
#linear fitting for solveing differential box dimension(DBC)
obj.execute(src)★ 子程序文件:DBC.py
import numpy as np
import cv2
import math
from matplotlib import pyplot as plt
class Fractal():
def __init__(self):
pass
# method of image graying
def gray(self, src):
gray_img = np.uint8(src[:,:, 0] * 0.144 + src[:, :, 1] * 0.587 + src[:, :, 2] * 0.299)
# cla_img = cv2.bilateralFilter(gray_img, 3, 64, 64)
# #clahe processing
# clahe = cv2.createCLAHE(clipLimit = 3, tileGridSize = (32, 32))
# cla_img = clahe.apply(bil_img)
return gray_img
# differential box dimension counting (DBC)
def differential_box_counting (self, gray_img):
h, w = gray_img.shape[:2]
M = min(h,w)
Nr = []
for s in range(2,M//2+1,1): # the box side length: 2 ~ M//2
H = 255*s/M # high of the box
box_num = 0 # initialization of the box number
for row in range(h//s): # h//s: the number of rows in the box; w//s: the number of columns in the box
for col in range(w//s):
nr = math.ceil((np.max(gray_img[row*s:(row+1)*s, col*s:(col+1)*s])-np.min(gray_img[row*s:(row+1)*s, col*s:(col+1)*s]))/H +1)
box_num += nr
Nr.append(box_num)
return Nr,M
def least_squares(self, x , y):
"""
(1) input datesets of x and y
(2) the straight line is fitted by Least-square method
(3) output a coefficient(w), intercept(b) and coefficient of determination (r)
(4) the fitting straight line : y = wx + b
"""
x_ = x.mean()
y_ = y.mean()
m1 = np.zeros(1)
m2 = np.zeros(1)
m3 = np.zeros(1)
k1 = np.zeros(1)
k2 = np.zeros(1)
k3 = np.zeros(1)
for i in np.arange(len(x)):
m1 += (x[i] - x_)* y[i]
m2 += np.square(x[i])
m3 += x[i]
k1 += (x[i]-x_) * (y[i]-y_)
k2 += np.square(x[i] - x_)
k3 += np.square(y[i] - y_)
w = m1/(m2 - 1/len(x) * np.square(m3))
b = y_ - w * x_
r = k1 / np.sqrt(k2 * k3)
return w, b, r
def plot_line(self, x, y, w, b, r):
# print(w, b, r ** 2)
y_pred = w * x + b
# create a fig and an axes
fig, ax = plt.subplots(figsize = (10, 5))
# fontsyle: SimHei(黑体),support chinese
plt.rcParams['font.sans-serif'] = ['SimHei']
ax.plot(x, y, 'co', markersize = 6, label = 'scatter datas')
ax.plot(x, y_pred, 'r-', linewidth = 2, label = 'y = %.4fx + %.4f' %(w, b))
# set xlim and yxlim
ax.set_aspect("0.5")
ax.set_xlim(1, 6)
ax.set_ylim(2, 12)
# set x_ticks and y_ticks
ax.tick_params(labelsize = 16)
labels = ax.get_xticklabels() + ax.get_yticklabels()
[label.set_fontname('Times New Roman') for label in labels]
# create grids
ax.grid(which = "major", axis = "both")
# display labels
font1 = {'family': 'Times New Roman', 'weight': 'normal', 'size': 16}
ax.legend(prop = font1)
#set x_label and y_label
font2 = {'family': 'Times New Roman', 'weight': 'normal', 'size': 20}
ax.set_xlabel("ln 1/r", fontdict = font2)
ax.set_ylabel("ln Nr", fontdict = font2)
# set a position of "R^2"
ax.text(3.5, 7.8, 'R^2 = %.4f' % float(r * r), fontdict = font1,
verticalalignment='center', horizontalalignment ='left', rotation=0)
plt.savefig("line.jpg", dpi = 300, bbox_inches = "tight")
plt.show()
def execute(self, img):
gray_img = self.gray(img)
Nr, M = self.differential_box_counting(gray_img)
x = np.log([round(M/s) for s in range(2,M//2+1,1)])
y = np.log(Nr)
#fitting a straight line
w, b, r = self.least_squares(x, y)
self.plot_line(x, y, w, b, r)
我们来看一下效果图:用最小二乘法进行拟合,斜率就是我们需要的维数.
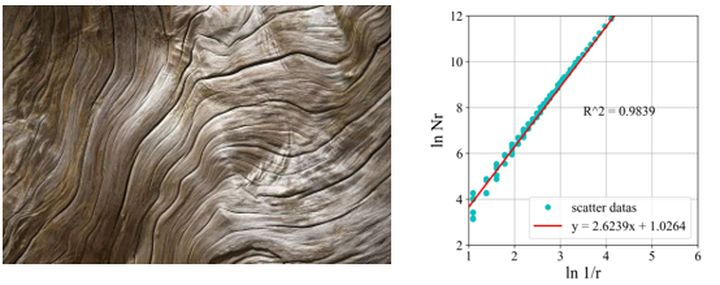
# 其实最小二乘法,也可以通过sklearn库直接调用.
import cv2
import numpy as np
import math
from matplotlib import pyplot as plt
from sklearn import linear_model
from sklearn.metrics import r2_score
from numba import jit
@jit
def differential_box_counting (gray_img):
# cv2.imshow("gray_img",gray_img)
h, w = gray_img.shape[:2]
M = min(h,w)
Nr = []
for s in range(2,M//2+1,1): #盒子边长从2到图片最小尺寸的二分之一,每次边长加1
H = 255*s/M #盒子柱高l
box_num = 0 #初始化盒子数
for row in range(h//s): #(h//s)为盒子的行数,(w//s)为盒子的列数
for col in range(w//s):
nr = math.ceil((np.max(gray_img[row*s:(row+1)*s, col*s:(col+1)*s])-np.min(gray_img[row*s:(row+1)*s, col*s:(col+1)*s]))/H +1)
box_num += nr
Nr.append(box_num)
return Nr,M
def Least_squares():
x = np.log([round(M/s) for s in range(2,M//2+1,1)])
x = np.array(x).reshape((-1, 1)) # transform list to numpy.ndarray
y = np.log(Nr)
y = np.array(y).reshape((-1, 1)) # transform list to numpy.ndarray
# Create linear regression object
regr = linear_model.LinearRegression() # is equivalent to # regr = linear_model.Ridge(alpha = 0)
# Train the model using the sets
regr.fit(x, y)
y_pred = regr.predict(x)
# The coefficients
print('Coefficients: ', regr.coef_)
#The intercept
print('Intercept: ', regr.intercept_)
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.8f'
% r2_score(y, y_pred))
plt.scatter(x, y, color='black')
plt.plot(x, y_pred, color='blue', linewidth=3)
plt.show()
if __name__ == "__main__":
gray_img = cv2.imread("D3.jpg", cv2.IMREAD_GRAYSCALE)
# thresh = cv2.threshold(gray_img, 220, 255, cv2.THRESH_BINARY)[1]
Nr,M = differential_box_counting(gray_img)
Least_squares()喜欢的话,给予鼓励,点个赞...
版权声明:本文为weixin_35717340原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。