定义

最简单的最常用的数据结构，以排队的方式去组织数据

线性，就是像线一样，前面是谁，后面是谁，串联好的次序

一对一：每个数据前面只能有一个数据，后面也只能有一个数据。前面没数据的就是起点，后面没数据的就是终点。

官方概念：线性表是0个或多个数据元素的有限序列。（0个元素则叫做空表）

线性表的一个数据元素可以有多个数据项。

操作

这里只写了一些最基本的使用最普遍的，实际上不同的应用中，需要线性表的操作可能多种多样，但是一般都可以用下面这些基本操作的组合来实现。
比如A和B两个线性表的并就是把A和B两个表的元素都插入到一个新的线性表中，但是重复项只插入一次

创建，初始化：建立一个空的线性表
重置为空表
查找：根据数据的位序找到数据元素，就像数组根据索引找值
查找某个元素是否存在
获得线性表的长度
插入一个数据
删除一个数据

//操作，没写返回值，其中参数为指针的都可以改为引用或者按值传递
InitList(*L);//参数是指向List的指针
IsListEmpty(*L);//如果为空，返回true
ClearList(*L);//清空重置
GetElem(*L, index, *e);//把线性表中index处的内容给e指向的位置
LocateElem(*L, e);//查找线性表中有无元素e,如果有，返回位置（索引），否则返回0
ListInsert(*L, index, e);//在index处插入元素e
ListDelete(*L, index, *e);//删除线性表的index处的元素，放入e指向位置
ListLength(*L);//返回元素个数，即线性表长度

假设把线性表A和B的union放入A：

void ListUnion(*La, *Lb)
{
	unsigned int len_a = ListLength(*La);
	unsigned int len_b = ListLength(*Lb);
	ElemType e;
	int i;
	for (i = 0; i < len_b; ++i)
	{
		GetElem(*Lb, i, *e);//这里只是伪代码，注意实际中不能这样，没初始化就解引用
		if (!LocateElem(*La, e))
		{
			ListInsert(*La, ++len_a, e);
		}
	}
}

两种物理结构

在这里插入图片描述

顺序存储结构

在这里插入图片描述

关键词：地址连续，每个数据元素的数据类型都一样

用一维数组实现顺序存储结构的线性表

描述顺序存储结构需要三个属性：

起始位置
线性表最大存储容量
线性表当前长度（小于等于最大长度）

可以用C语言实现，或者其他语言：

typedef int Type;//增加代码的通用性
const int MAXSIZE = 10;//最大容量
typedef struct
{
	Type data[MAXSIZE];//data数组名，就是起始位置
	int length;//当前长度
}SqList;

随机存取结构：存取时间性能是 0(1)的存储结构

由于一维数组这种线性表的起始位置知道，地址又连续，所以其中任意位置的地址可以被很简单地立即算出，用时间复杂度的概念来说就是:存取时间性能是O（1）。

这种存储结构我们就成为随机存储结构。

所以顺序结构的线性表是一种随机存储结构。

获得元素操作（非常简单）

对于顺序结构的线性表，返回某个位置的元素非常简单，这就是随机访问，因为顺序存储线性表就是随机存储结构。

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;

Status GetElem(SqList L, int i, ElemType *e)
{
	if (L.length == 0 || i < 0 || i > L.length)
		return ERROR;
	*e = L.data[i];
	return OK;
}

插入操作（复杂）

在这里插入图片描述

Status ListInsert(SqList * L, int i, ElemType e)
{
	int k;
	if (L->length == MAXSIZE)
		return ERROR;
	if (i < 0 || i > L->length)
		return ERROR;
	if (i < L->length - 1)//插入位置不在表尾
	{
		for (k = L->length-2;k>=i;k--)
			L->data[k+1] = L->data[k];
	}
	L->data[i] = e;//插入新元素
	L->length++;
	return OK;
}

复杂度：

最好情况：插入位置是线性表的末尾，不需要移动元素，所以复杂度O(1)
最坏情况：插入位置是线性表的起始位置，即第一个位置，需要所有元素后移一步，所以复杂度O(n),n是线性表长度
平均情况：插入到第i个位置，需要移动n-i个元素，如果i靠前，则移动的元素就多，反之反之。平均起来，i取n/2，则复杂度 $O(\frac{n-1}{2})$ ,忽略常数，即仍然是O(n).

所以，线性表的顺序存储结构在存入或者读取数据时的复杂度是O(1);在插入或者删除数据的复杂度是O(n).所以他很适合不经常插入和删除，而是经常读取和存入（不是插入）的应用场景。

删除操作

队列长度如果为0，抛出异常
再看索引范围是否正确，删除位置不合理则抛出异常
取出删除元素
从索引i+1开始，一直到length-1的元素全部往前移动一位
长度减1

Status DeleteList(SqList * L, int i, ElemType & e)
{
	int k;
	if (L->length == 0)
		return ERROR;
	if (i < 0 || i > L->length-1)
		return ERROR;
	e = L->data[i];//取出元素，这里由于要保证函数执行完毕后e的值不丢失，使用引用类型
	for (k = i + 1; k < length; ++k)
	{
		L->data[k-1] = L->data[k];
 	}
 	L->length--;
 	return OK;
}

删除操作的算法复杂度和插入一毛一样。

优缺点

在这里插入图片描述
优点第一点：比如链表就需要除了数据项以外，还要给一个指针分配空间，用于指向下一个数据项的位置。

链式存储结构：“乱”中有“序”

如图，物理内存位置乱七八糟，不像顺序结构那样紧紧挨着排成一列，非常集中，可以相邻也可以不相邻，是一种动态的零散的结构；但是逻辑位置却又十分有序，是一个线性的单链。我觉得乱中有序来形容链表，双重意味，最贴切不过。

在这里插入图片描述

但是链式结构需要额外空间存储下一个元素的地址，不仅要处处数据项。存数据的域叫做数据域，存后继元素地址的域叫做指针域。这两部分组合在一起，成为一个数据元素的存储映像，被称为结点Node.
在这里插入图片描述

单链表：结点只有一个指针域

如果每个结点只有一个指针域，就叫做单链表。因为这唯一的一个指针域中存储的是指向后继结点的指针next，只能访问后继结点，所以是单向的。

头指针：指向第一个元素，不可能为空指针

第一个结点的内存位置叫做头指针，即指向第一个元素

就算链表是空的，头指针也不可能是空的,因为头指针一定会指向第一个结点，如果是空链表，也会有第一个结点，只不过第一个结点的数据域不存东西，指针域存空指针（这就表示这个结点也是最后一个结点）。

他是链表的必需元素，不能没有

但是如果链表有头结点，则头指针是头结点指针域中存储的那个指针

尾指针：NULL，空指针

在这里插入图片描述

头结点(可以没有但一般都会用，因为它可以让空链表和非空链表的处理一致)

有时候会专门给链表附加一个头结点，不是为了存储数据，只是为了操作方便和统一设立的，数据域可以不存东西，也可以存整个链表的长度信息。

方便：可以直接获取到链表长度，无需遍历一次
统一：有了头结点，则对第一个元素前面插入元素，以及删除第一个元素的操作，就和其他节点一致了;且头结点使得所有链表（即使是空链表）的头指针都不为空指针(空链表的头结点的指针域中的指针为空指针)。这种统一性是头结点带来的最大的好处。

当有头结点的时候，头指针指向头结点，头结点指针域的指针指向第一个常规结点；

没有头结点的时候，头指针指向第一个常规结点（存储数据）。

头指针并不是头结点的指针域中的内容！

没有头结点的单链表（头指针指向第一个常规结点，尾结点指针域的符号表示空指针）
有头结点的单链表（头指针指向头结点，头结点指针域的指针指向第一个常规结点）
头结点的数据域是黑色代表没有数据项，但是可以存其他附加信息

在这里插入图片描述

有头结点的空链表（头指针指向头结点，头结点指针域的指针指向第一个常规结点）

这时候头结点的指针域存储空指针

所以头结点的好处是：使得空链表中头指针也不为空指针！！空链表的头结点的指针域中的指针为空指针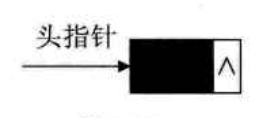
在这里插入图片描述

用C的结构实现结点

typedef struct
{
	ElemType data;//数据域
	Struct Node * next;//指针域
}Node, *LinkList;

//typedef struct Node * LinkList;

如果p是一个指针，且p->data = $a_i$ ,则p->next->data= $a_{i+1}$

获取元素操作:遍历，指针右移

只能遍历，一个一个找。核心就是利用指针的右移一个一个地遍历，其实很多算法都要用到这种技术。
在这里插入图片描述

Status GetElem(LinkList L, int i, ElemType & e)
{
	LinkList p = L->next;//L是头指针，指向头结点，p被初始化为第一个结点的地址,即指向第一个结点
	int j = 0;
	while (p && j < i)
	{
		p = p->next;
		++j;
	}
	if (j == i)
	{
		e = p->data;
		return OK;
	}
	return ERROR;//无此数据
}

算法时间复杂度取决于i的位置：
最好情况，i=0，则立刻就找到了，不需要遍历
最坏情况，i=n-1，n为链表长度，则需要遍历n-1次，最坏情况时间复杂度是O(n)

插入和删除

都是先遍历找到索引为i的元素，然后插入或者删除。时间复杂度也和i的位置有关，i=0是最好情况，无需遍历，最坏情况i=n-1，光遍历的时间复杂度就是O(n)，但是插入和删除的核心操作都只是一句代码的事，时间复杂度是O(1)。

所以插入和删除的时间复杂度总的来说都是O(n)，主要时间都花在遍历上了。

插入操作

在这里插入图片描述

s->next = p->next;
p->next = s;

在这里插入图片描述

Status InsertItem(LinkList L, int i, ElemType e)
{
	LinkList s;
	LinkList p = L->next;//L指向头结点，p指向第一个结点
	int j = 0;
	while (p && j < i)
	{
		p = p->next;
		++j;
    }
    if (!p)
    	return ERROR;
    LinkList s = new LinkList;//C++可以在任何位置声明变量
    //C形式,要在函数最前面声明s
    //s = (LinkList)malloc(sizeof(Node));
    
    s->data = e;
    s->next = p->next;//p现在指向第i-1个元素
    p->next = s;
    return OK;
}

删除操作

在这里插入图片描述

Status DeleteItem(LinkList L, int i, ElemType * e)
{
	//L是头结点中存的指针，指向第一个常规结点
	LinkList p = L->next;
	int j = 0;
	while (p->next && j < i)
	{
		p = p->next;
		++j;
	}
	if (!(p->next))
		return ERROR;
	LinkList q = p->next;//必须用q存住p->next以释放它
	*e = p->next->data;
	p->next = p->next->next;//核心代码就这一句
	free(q);
	return OK;
}

单链表的动态创建

顺序结构的线性表的创建，实际上就是初始化一个数组，只需要告诉数组元素的数据类型和数组长度；

但是链表是动态结构，事先不知道链表长度，所以不能事先分配，只能根据需求即时生成一个结点并插入到链表中。

头插法：把新结点插在头结点后面，做第一个常规结点

每次把新结点插在头结点后面。做第一个常规结点。

void CreateListHead(LinkList *L, int n)
{
	//L是指向头指针(*L)的指针，因为LinkList 是struct Node *
	//n是要创建的项数
	LinkList p;
	int i;
	srand(time(0));//设置随机数种子
	//先创建空链表：只有头结点，且头结点的指针域中存空指针
	*L = (LinkList)malloc(sizeof(Node));//*L是头指针，指向刚分配的结点：头结点
	(*L)->next = NULL;//空链表创建成功

	for (i = 0; i < n; ++i)
	{
		//生成新节点
		p = (LinkList)malloc(sizeof(Node));
		p->data = rand() %100 + 1;
		//把新节点p插入到第一个位置
		p->next = (*L)->next;
		(*L)->next = p;
	}
}

彻底被这几个指针搞晕了，拿了纸笔一通分析，得到以下结论：

L是指向头指针的指针，头指针指向头结点，头结点的指针域中存的指针指向第一个常规结点！，L是LinkList *类型
*L是头指针，指向头结点，而头结点的指针域中存的那个指针指向第一个结点（非头结点，第一个存内容的常规结点）。*L，解引用一下，是LinkList类型，即struct Node *类型。
**L是头结点。对*L再解引用一下，得到Node类型。

我画了个草图：
在这里插入图片描述

尾插法

每次把新结点插在前一个新结点后面，即终端节点的后面，先来后到。

这里要用一个指向尾结点的指针rear

void CreateListTail(LinkList * L, int n)
{
	LinkList p, r;
	int i;
	srand(time(0));
	//先创建空链表
	*L = (LinkList)malloc(sizeof(Node));
	(*L)->next = NULL;
	r = *L;//指向尾结点
	
	//循环创建新结点，并随机给数据域赋值
	for (i = 0; i < n; ++i)
	{
		p = (LinkList)malloc(sizeof(Node));//新结点
		p->data = rand()%100 + 1;
		r->next = p;
		r = p;
	}
	r->next = NULL;
}

在这里插入图片描述

单链表的整表删除：在内存中释放掉它占用的空间

由于链表的每一个结点都是动态创建的，是动态分配地堆内存，所以删除链表必须要释放每一个结点的地址，否则就会有内存泄漏的危险。

考虑挨个释放，先把第一个free，问题来了，第二个结点在哪儿都不知道了······因为第二个结点的位置在第一个结点里。所以:

声明新结点p和q
把第一个结点赋给p
循环：

把下一结点给q
释放p
把q赋给p

Status ClearList(LinkList *L)
{
	//*L是头指针
	LinkList p, q;
	p = (*L)->next;//p指向第一个结点
	while (p)
	{
		q = p->next;
		free(p);
		p = q;
	}
	//至此p为空指针
	(*L)->next = NULL;//头结点的指针域存储空指针，表示空链表
	return OK;
}

顺序结构和单链表结构的对比

在这里插入图片描述

说白了就是单链表更灵活。

顺序结构的唯一优点：查找快。如果非要再加一个，那就是代码不好写点。

单链表的唯一缺点：查找慢。如果非要再加一个，那就是代码好写点。

这么看的话，我还是乖乖用链表吧。

当然，我上面两句总结有些偏颇，不能说链表就一定比顺序结构的数组好，要看应用场景，有时候还真是数组合适一些。

在这里插入图片描述

原文链接：https://blog.csdn.net/qq_36607894/article/details/105281530

m数据结构 day2 线性表List（一）数组，单链表

文章目录

定义

操作

两种物理结构

顺序存储结构

用一维数组实现顺序存储结构的线性表

随机存取结构：存取时间性能是 0(1)的存储结构

获得元素操作（非常简单）

插入操作（复杂）

删除操作

优缺点

链式存储结构：“乱”中有“序”

单链表：结点只有一个指针域

头指针：指向第一个元素，不可能为空指针

尾指针：NULL，空指针

头结点(可以没有但一般都会用，因为它可以让空链表和非空链表的处理一致)

用C的结构实现结点

获取元素操作:遍历，指针右移

插入和删除

插入操作

删除操作

单链表的动态创建

头插法：把新结点插在头结点后面，做第一个常规结点

尾插法

单链表的整表删除：在内存中释放掉它占用的空间

顺序结构和单链表结构的对比