完成了我们的专题1——树 部分的刷题练习之后 我们(终于!)来到了第二部分:数组与字符串
经历了专题1大量题目洗礼过后的我们 应该变得对刷题更有自信了!(没看过专题1的内容不妨回去看一眼~)那么 我们继续!
【1】先对
LeetBook中的内容进行一个学习
数组是数据结构中的基本模块之一。- 因为
字符串是由字符数组形成的,所以二者是相似的。
——我们面临的大多数面试问题都属于这个范畴。要刷的题目涉及如下专题——
(1)专题1 理解数组的基本概念及其操作方式;
(2)专题2 理解二维数组的基本概念,熟悉二维数组的使用;
(3)专题3 了解字符串的概念以及字符串所具有的不同特性;理解字符串匹配中的KMP 算法;
(4)专题4 能够运用双指针解决实际问题。
【2】在解决
LeetBook中推荐的题目的过程中 我发现了非常有趣的两个专题——
(1)专题5 前缀和思想求解子数组&子串问题
(2)专题6 二分查找数组中元素问题
文章目录
本专题有三道题
都是需要通过一定的数学知识 找到规律 然后利用循环解题!
[2]二维数组简介
多维数组适合像表/矩阵这样更复杂的结构
本章中我们围绕二维数组解释——
- 二维数组在内存中是如何存放的
- 如何运用二维数组来解决问题
二维数组是一种结构较为特殊的数组,只是将数组中的每个元素变成了一维数组。
所以二维数组的本质上仍然是一个一位数组
另外 其内部的一位数组仍然从索引0开始
我们可以将它看作一个矩阵 并处理矩阵的相关问题
示例
类似一维数组,对于一个二维数组 A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]]
计算机同样会在内存中申请一段 连续 的空间,并记录第一行数组的索引位置 即 A[0][0] 的内存地址
它的索引与内存地址的关系如下图所示——
注意 实际数组中的元素由于类型的不同 会占用不同的的字节数 因此每个方格地址之间的差值可能不为1
实际题目中 往往使用二维数组处理矩阵类相关问题
包括矩阵旋转 对角线遍历 以及对子矩阵的操作等
做三道题练习一下二维数组 都是围绕着矩阵来玩儿~
面试题 01.07. 旋转矩阵 medium
本题与主站 48 题 旋转图像相同:
给你一幅由 N × N 矩阵表示的图像,其中每个像素的大小为 4 字节。请你设计一种算法,将图像旋转 90 度。
不占用额外内存空间能否做到?
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
解题思路
【1】使用 辅助数组 这个应该就是easy级别的做法了
诶就很简单
需要注意的是
题目的输入是一个数组 最后返回的也是这个数组
所以最后需要把辅助数组的内容全部赋给输入的数组(这个一开始没注意到 结果一跑结果发现 诶 为啥没变化)
复杂度分析
- 时间复杂度:O(N2),其中 N 是 matrix的边长。
- 空间复杂度:O(N2),我们需要使用一个和 matrix 大小相同的辅助数组。
【2】原地旋转 medium级别的高级
以下方法都参考了官方题解辽
想不出来不用辅助数组的方法嘤嘤嘤
详情康官方题解吧~这里就不复现了
【3】用翻转代替旋转 medium级别的更好想的做法
(但还是好难想呐!小声bb)
步骤为:
【1】先根据水平轴翻转
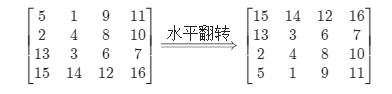
【2】再根据主对角线翻转
为啥?
因为经过这两步操作之后 发现得到了一个很眼熟的公式
做题的时候把图画出来 会更好想哦~
注意对角线翻转的写法 第一次就很智障地写错了。跑完发现结果和水平翻转完恰好一样 才发现给的测试用例恰好就满足这么个情况…
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){//注意是i嗷
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
- 时间复杂度:O(N2),其中 N 是 matrix的边长。对于每一次翻转操作 我们都需要枚举矩阵中一半的元素
- 空间复杂度:O(1),为原地翻转得到的原地旋转。
Java代码
【1】辅助数组法
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
int[][] matrix_new = new int [n][n];//初始化二维数组(有数组长度的情况下)
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix.length; j++) {
matrix_new[i][j] = matrix[n - j - 1][i];
}
}
//把辅助数组的的内容赋给结果数组
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix.length; j++) {
matrix[i][j] = matrix_new[i][j];
}
}
}
}
很简单的方法 试几个数就出来了嗷
【2】官方题解:用翻转操作代替旋转操作
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//水平翻转
for(int i = 0; i < n /2; i++){
for(int j = 0;j < n; j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = temp;
}
}
// 根据主对角线翻转
for(int i = 0; i < n; i++){
for(int j = 0; j < i; j++){//注意这里是j<i 嘤嘤嘤 你沿对角线翻转再错就打你脑袋,
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
}
面试题01.08.零矩阵 medium
时隔5天之后 重新开始刷题!规律学习生活!启动!
编写一种算法,若M × N矩阵中某个元素为0,则将其所在的行与列清零。
示例 1:
输入:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
输出:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
示例 2:
输入:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
输出:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
解题思路
我的方法
比较笨的一个方法
但是比较好想哈哈哈
写了三个循环
注释里都说明原因了
另外主要是因为本做法是这样想的——看到有等于0的元素 就把对应的位置全改成0
这就会造成 “改了一个0之后 它继续辐射影响周围本不应该是0的位置”
所以——只能整一个辅助数组先存一下原数组之后再赋值过去。
与官方题解的方法一——
方法一:使用标记数组
我们可以用两个标记数组分别记录每一行和每一列是否有零出现。
具体地,我们首先遍历该数组一次,如果某个元素为 0,那么就将该元素所在的行和列所对应标记数组的位置置为 true。最后我们再次遍历该数组,用标记数组更新原数组即可。
class Solution { public void setZeroes(int[][] matrix) { int m = matrix.length, n = matrix[0].length; boolean[] row = new boolean[m]; boolean[] col = new boolean[n];//这两个标记数组用的比我的方法巧妙多了hhh for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (matrix[i][j] == 0) { row[i] = col[j] = true; } } } for (int i = 0; i < m; i++) { for (int j = 0; j < n; j++) { if (row[i] || col[j]) {//只要这个位置沾上了“和0元素同行 row[i] = true" 或 ”和0元素同列 col[i] = true“ //就把 matrix[i][j] = 0; } } } } }
比较类似
时间复杂度:
O(mn),其中 m 是矩阵的行数,n 是矩阵的列数。我们至多只需要遍历该矩阵两次。空间复杂度:
O(m+n),其中 m 是矩阵的行数,n 是矩阵的列数。我们需要分别记录每一行或每一列是否有零出现。
官方题解达到O(1)
Java代码
我的方法
//这个方法不够巧妙!虽说很好想 但是不建议使用!看上面那个官方题解一 (使用标记数组)更巧妙
//没想到使用俩标记数组做一个“0元素具体位置”的存储是我的问题QAQ
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
int[][] matrix_new = new int [m][n];//整一个辅助数组
// 把原始数组的值赋给辅助数组
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
matrix_new[i][j] = matrix[i][j];
}
}
// 将原始数组中为0的值找出来 并把辅助数组中对应的行和列全部赋0
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(matrix[i][j] == 0){
for(int a = 0; a < n; a++){
// 第i行的全赋0
matrix_new[i][a] = 0;
}
for(int b = 0; b < m; b++){
// 第j列的全赋0
matrix_new[b][j] = 0;
}
}
}
}
// 把辅助数组的值再赋给要返回的那个数组
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
matrix[i][j] = matrix_new[i][j];
}
}
}
}
达到O(1)
498.对角线遍历 medium
给定一个含有 M x N 个元素的矩阵(M 行,N 列)
请以对角线遍历的顺序返回这个矩阵中的所有元素,对角线遍历如下图所示。
示例:
输入:
[
[ 1, 2, 3 ],
[ 4, 5, 6 ],
[ 7, 8, 9 ]
]
输出: [1,2,4,7,5,3,6,8,9]
解释:

解题思路
先点出来
int m = matrix.length;//行数
int n = matrix[0].length;//列数
首先考虑了要走多少趟—— m + n - 1趟
再分奇数偶数讨论一下
举几个例子
【1】三行三列
【2】三行四列
最后也没搞出来答案。这块儿规律确实是有点难找
参考大佬的题解
【对角线遍历】小白看过来,最直白易理解版本!!手把手解释代码!!!
关键就是找边界
Java代码
class Solution {
public int[] findDiagonalOrder(int[][] mat) {
int row = mat.length;//行数
int col = mat[0].length;//列数
int count = row + col - 1;一共会走row+col-1趟
int[] ans = new int[row * col];
int ansIndex = 0;
int a = 0;
int b = 0;//a b 代表横纵坐标 控制奇数偶数的趟数
//只要横坐标不减到负数,纵坐标不大于列数 往数组添加元素的动作就可以继续下去,
//一共会走row+col-1趟
// 偶数趟是先打印上面的
for(int i = 0; i < count; i++){
if(i % 2 == 0){
while(a >= 0 && b < col){
ans[ansIndex] = mat[a][b];
ansIndex++;
a--;
b++;
}
if(b < col){
a++;
}
else{
a = a + 2;
b--;
}
}
// 奇数趟是 先打印底下的
else {
while(a < row && b >= 0){
ans[ansIndex] = mat[a][b];
ansIndex++;
a++;
b--;
}
if(a < row){
b++;
}
else{
a--;
b = b + 2;
}
}
}
return ans;
}
}

