树是一种非线性结构的数据结构,有一个点没有前驱,被称为根节点,它可以有多种变化,普通二叉树,N叉树,二叉搜索树(BST),红黑树(RBTree),B树等等,上述所说的树中,普通二叉树就算是比较简单的数据结构。
二叉树的存储:
二叉树的存储方式分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式。
我们使用孩子表示法来给大家解释一下
class TreeNode {
public char val;//数据
public TreeNode left;//左孩子的引用,常常代表左孩子为根的整棵左子树
public TreeNode right;// 右孩子的引用,常常代表右孩子为根的整棵右子树
}还有一种孩子双亲表示法,我们这里不进行过多介绍。
树的遍历:
树的遍历分为四种:先序遍历,中序遍历,后序遍历,层序遍历。
我们一般用递归来求遍历结果,如果想要用迭代来求递归结果需要借用栈或者队列来进行求解。
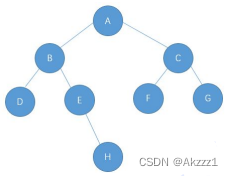
先序遍历:先序遍历的遍历顺序是 根→左→右的顺序打印,我们先打印根节点,在打印左孩子,最后打印右孩子,如上图,我们先打印A,然后打印B,发现B也有左孩子,之后我们以B为根节点再进行一次跟左右遍历,打印D,之后我们准备打印B的右孩子就是E,发现E有右孩子,所以我们这边又以E作为根节点,进行跟左右操作,以此类推,得到最后的结果是:ABDEHCFG。
中序遍历:先序遍历的遍历顺序是 左→根→右的顺序打印,我们一开始准备打印A的左孩子B,发现B也有左孩子然后以B为根节点进行左→根→右进行打印,所以我们一开始打印的是D这个节点,中序遍历和先序遍历的思维差不多,无非就是打印顺序的调整。最后的结果为:DBEHAFCG。
后序遍历:先序遍历的遍历顺序是 左→右→根的顺序打印,跟前面两种遍历方式类似,就是打印的顺序不同,我们应该先遍历完左右孩子再进行根节点的打印。最后的结果是:DHEBFGCA。
层序遍历:层序遍历就比较简单,层序遍历就是按照各层顺序打印结果,如上图的层序遍历就是:ABCDEFGH。
遍历我们一般用递归方式,以下是递归方式实现的前中后序的遍历代码:
//前序遍历
void preOrderTraversal(TreeNode root) {
if (root == null) {
return;
} else {
System.out.print(root.val + " ");
preOrderTraversal(root.left);
preOrderTraversal(root.right);
}
}
//中序遍历
void inOrderTraversal(TreeNode root) {
if (root == null) {
return;
} else {
inOrderTraversal(root.left);
System.out.print(root.val + " ");
inOrderTraversal(root.right);
}
}
//后序遍历
void poseOrderTraversal(TreeNode root) {
if (root == null) {
return;
} else {
poseOrderTraversal(root.left);
poseOrderTraversal(root.right);
System.out.print(root.val + " ");
}
}我们也可以使用迭代来实现前中后序的递归,我们利用栈这个数据结构来辅助我们实现遍历。
//非递归的前序遍历
void preOrderTraversalNor(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
System.out.print(cur.val + " ");
cur = cur.left;
}
TreeNode top = stack.pop();
cur = top.right;
}
}
//非递归的中序遍历
void inOrderTraversalNor(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
TreeNode top = stack.pop();
System.out.print(top.val + " ");
cur = top.right;
}
}
//非递归的后序遍历
void poseOrderTraversalNor(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
TreeNode cur = root;
while (cur != null || !stack.empty()) {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.peek();
if (cur.right == null||pre==cur.right) {
TreeNode top = stack.pop();
System.out.print(top.val+ " ");
pre=cur;
cur=null;
} else {
cur=cur.right;
}
}
}层序遍历我们一般使用迭代来实现,我们利用队列这个数据结构来辅助我们。
void levelOderTraversal(TreeNode root) {
Queue<TreeNode> q1 = new LinkedList<>();
if (root == null) {
return;
}
q1.offer(root);
while (!q1.isEmpty()) {
TreeNode top = q1.poll();
System.out.print(top.val + " ");
if (top.left != null) {
q1.offer(top.left);
}
if (top.right != null) {
q1.offer(top.right);
}
}
System.out.println();
}