并查集是一种树型的数据结构,用于处理一些不相加集合的合并和查询问题。在使用中常常以森林来表示。 并查集也是用来维护集合的,和前面学习的set不同之处在于,并查集能很方便地同时维护很多集合。如果用set来维护会非常的麻烦。并查集的核心思想是记录每个结点的父亲结点是哪个结点。

1) 初始化:初始的时候每个结点各自为一个集合,father[i]表示结点 i 的父亲结点,如果 father[i]=i,我们认为这个结点是当前集合根结点。

void init() {
    for (int i = 1; i <= n; ++i) {
        father[i] = i;
    }
}

2) 查找:查找结点所在集合的根结点,结点 x 的根结点必然也是其父亲结点的根结点。

int get(int x) {
    if (father[x] == x) { // x 结点就是根结点
        return x; 
    }
    return get(father[x]); // 返回父结点的根结点
}

3) 合并:将两个元素所在的集合合并在一起,通常来说,合并之前先判断两个元素是否属于同一集合。

void merge(int x, int y) {
    x = get(x);
    y = get(y);
    if (x != y) { // 不在同一个集合
        father[y] = x;
    }
}

上面三个操作是并查集常用的操作

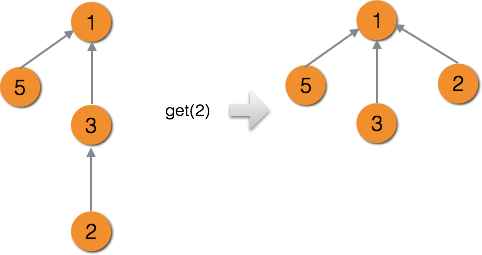
前面的并查集的复杂度实际上在有些极端情况会很慢。比如树的结构正好是一条链，那么最坏情况下，每次查询的复杂度达到了O(n) 。这并不是我们期望的结果。路径压缩的思想是，我们只关心每个结点的父结点，而并不太关心树的真正的结构。

这样我们在一次查询的时候，可以把查询路径上的所有结点的father[i]都赋值成为根结点。只需要在我们之前的查询函数上面进行很小的改动

int get(int x) {
    if (father[x] == x) { // x 结点就是根结点
        return x; 
    }
    return father[x] = get(father[x]); // 返回父结点的根结点，并另当前结点父结点直接为根结点
}

路径压缩在实际应用中效率很高,其一次查询复杂度平摊下来可以认为是一个常数。并且在实际应用中,我们基本都用带路径压缩的并查集。

带权并查集

所谓带权并查集，是指结点存有权值信息的并查集。并查集以森林的形式存在，而结点的权值，大多是记录该结点与祖先关系的信息。比如权值可以记录该结点到根节点的距离。

例题

在排队过程中，初始时，一人一列。一共有如下两种操作。

• 合并：令其中的两个队列 A，B 合并，也就是将队列 A 排在队列 B 的后面。
• 查询：询问某个人在其所在队列中排在第几位。

例题解析
我们不妨设 size[]为集合中的元素个数，dist[]为元素到队首的距离，合并时，dist[A.root]需要加上size[B.root] (每个元素到队首的距离应该是到根路径上所有点的dist[]求和)，size[B.root]需要加上size[A.root] (每个元素所在集合的元素个数只需查询该集合中根的size[x.root])。

1)初始化：

void init() {
    for(int i = 1; i <= n; i++)  {
        father[i] = i, dist[i] = 0, size[i] = 1;
    }
}

2)查找：查找元素所在的集合，即根节点。

int get(int x) {
    if(father[x] == x) {
        return x;        
    }
    int y = father[x];
    father[x] = get(y);
    dist[x] += dist[y];  // x 到根结点的距离等于 x 到之前父亲结点距离加上之前父亲结点到根结点的距离
    return father[x];
}

路径压缩的时候，不需要考虑 size[]，但 dist[] 需要更新成到整个集合根的距离。

3)合并
将两个元素所在的集合合并为一个集合。

通常来说，合并之前，应先判断两个元素是否属于同一个集合，这可用上面的“查找”操作实现。

void merge(int a, int b) {
    a = get(a);
    b = get(b);
    if(a != b) {  // 判断两个元素是否属于同一集合
        father[a] = b;
        dist[a] = size[b];
        size[b] += size[a];
    }
}

通过小小的改动，我们就可以查询并查集这一森林中，每个元素到祖先的相关信息。

怎么样，明白些了吗？

我们来做一道题目吧！

找朋友

样例输入

6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

Yes
Yes
No

题解：：

#include<iostream>  
#include<algorithm>  
#include<string.h>  
using namespace std;  
int mark[5005],fa[5005];  
int get(int x)
{  
    if(fa[x]==x)
        return x;  
    return fa[x]=get(fa[x]);  
}  
int main()
{  
    int n,m,p;
    cin>>n>>m>>p;  
    int a,b;   
    memset(mark,0,sizeof(mark));  
    for(int i=1;i<=n;i++)
        fa[i]=i;  
    while(m--)
    {  
        cin>>a>>b;  
        a=get(a);  
        b=get(b);  
        if(a!=b)
        {  
            fa[a]=b;  
        }  
    }  
    for(int i=1;i<=p;i++)
    {  
        cin>>a>>b;  
        a=get(a);
        b=get(b);  
        if(a==b)
            mark[i]=1;  
    }  
    for(int i=1;i<=p;i++)
    {  
        if(mark[i])
            cout<<"Yes"<<endl;  
        else 
            cout<<"No"<<endl;  
    }  
    return 0;  
}

谢谢