Word2Vec Tutorial

Idea

Word2Vec 是一个可以将单词转换为固定维度向量的工具。

Two model

Skip-Gram(SG)
- 基本思想
  给定中心词，去预测窗口范围内的词。
  例如给定句子：{...,"prolems", "turning", ’into", ’banking", "crises’, "as",...}
  给定窗口 $m = 2$ ，中心词为 banking。
- 模型

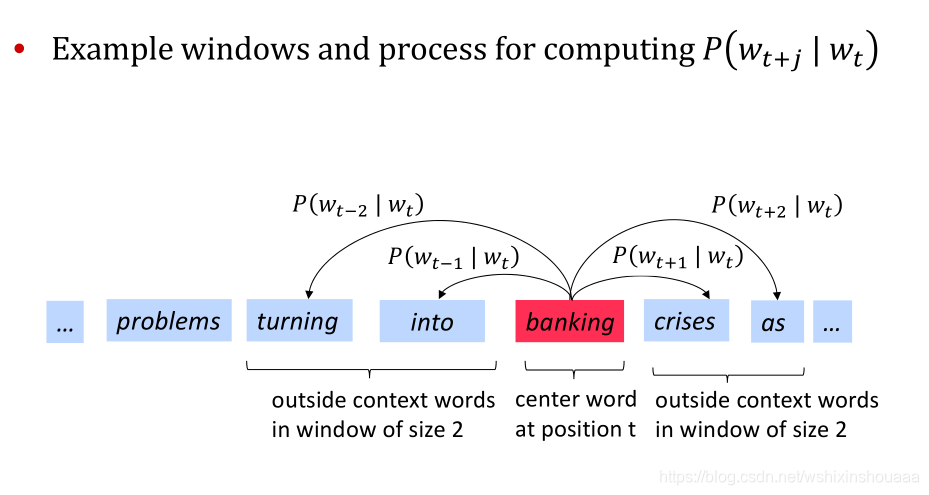
在这里插入图片描述

过程
- 参数
  在开始训练前，把所有的单词以 one-hot 向量表示，输入中心词 x 的时候就是输入该词的 one-hot 向量表示，在输出预测词 $y^{'} $ 的时候是一个概率向量，这个后面会讲，但是这个预测词对应的真实标签 $y $ 则是一个 one-hot 向量。
  每个词 $w_{i}$ 都分别有 $v_{i}$ 和 $u_{i}$ 两个向量表示：
  1. 当 $w_{i}$ 作为中心词输入时，使用 $v_{i}$ 参与计算；
  2. 当 $w_{i}$ 作为上下文词时，使用 $u_{i}$ 参与计算。
  所以还需要两个重要的矩阵 $V $ 和 $U $ ，即模型图中的权重矩阵 $W_{V*N}$ 和 $W'_{N*V} $ ：
  $n $ 是设定好词向量的维度。
  数组 $V $ 如下图所示：
  
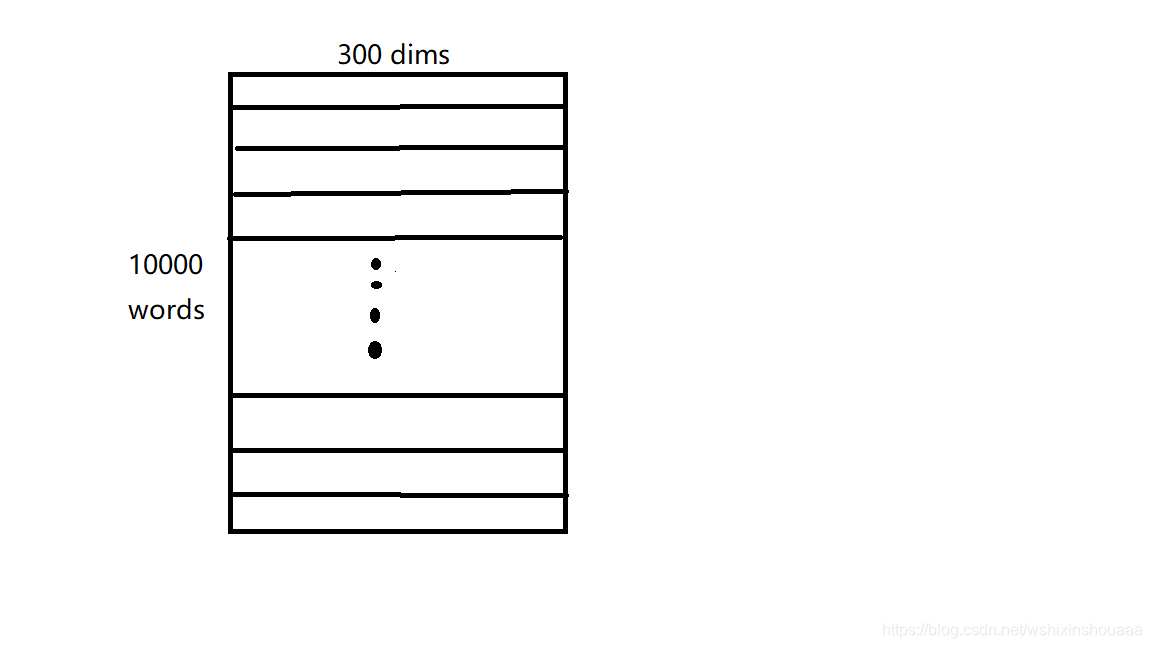
  数组 $U $ 如下图所示：
- 前向过程
- 后向过程
  1. 目标函数
    单词个数为 $T$ ，窗口大小为 $m$ ，所有单词的向量表示为 $\theta$ 。
    目的是通过训练得到合适的 $\theta$ ，最大化似然函数 $L(\theta)$ ，即最小化负的对数似然函数 $J(\theta)$ 。
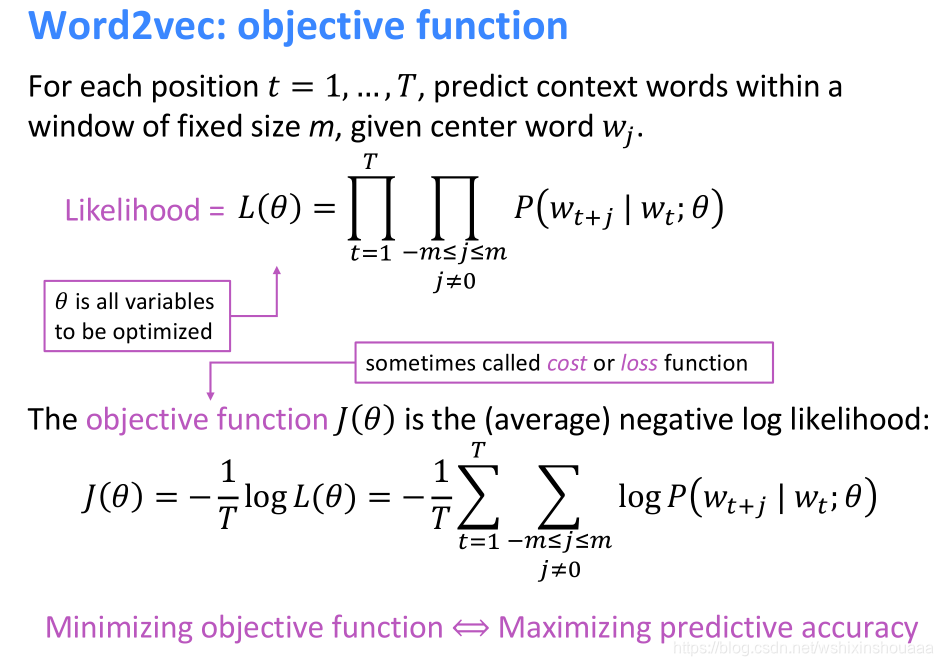
  2. 推导过程
    对中心词求导：
  1. 使用梯度优化算法更新所有的词向量 $u_{c}$ 和 $v_{j}$ 。
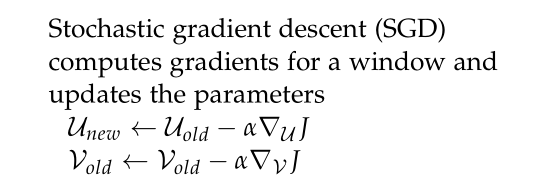
Continuous Bag of Words(CBOW)
- 基本思想
  给定窗口范围内的词，去预测窗口中间的词。
  例如句子：{"The", "cat", ’jumped", ’over", "the’, "puddle"}，窗口大小为 2 ，预测 jump的概率。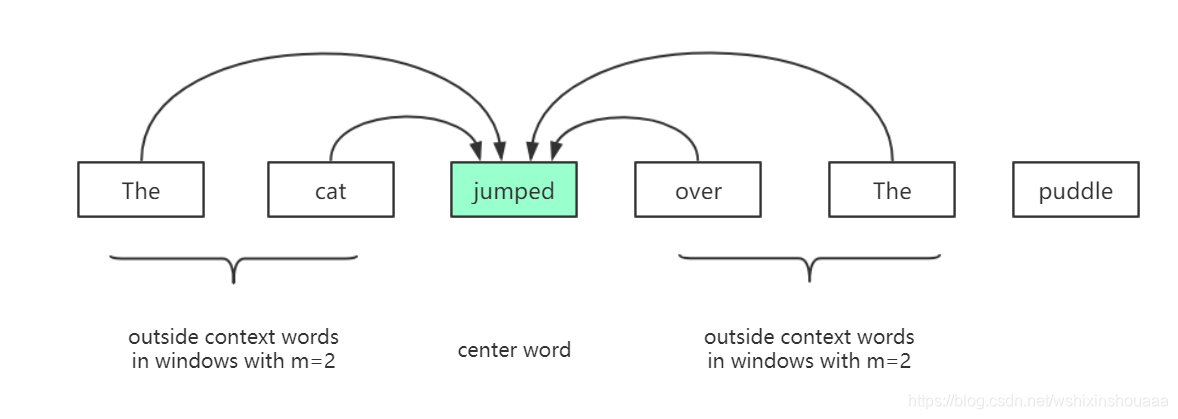
- 本质
  依次计算输入的中心词 $v_{c}$ 与窗口内的上下词 $u_{o}$ 的点积相似度(可换成余弦相似度)，并进行 Softmax 归一化。
- 模型
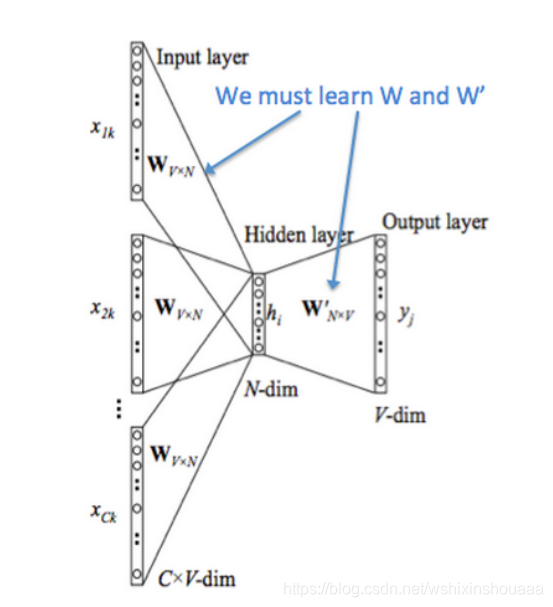
  单词的个数为 $V$ ，单词向量空间维度为 $N$ ，上下文单词的个数为 $C$ 。
- 过程
  - 前向过程
    简单来说：
    1. 输入是 C 个上下文词的 one-hot 向量，大小为 $C$ 个 $[1, V]$ 的向量。
    2. 分别将每个 one-hot 向量与权重矩阵 $W_{V*N}$ 进行点积操作，得到 $C$ 个 $[1, N]$ 的向量，然后累加求平均为一个向量，作为隐层向量的表示。实质上是根据 one-hot 向量中 1 的位置从 $W_{V*N}$ 中取出每个单词的向量进行累加，融合为一个可以表示这些词的总向量。
    3. 将得到的矩阵与权重矩阵 $W'_{N*V}$ 进行点积操作，得到大小为 $[1, V]$ 的矩阵。实质上是将第二步得到的C个词总向量与 $W'_{N*V}$ 中的每一列（每一个单词的向量表示）做点积相似度计算。
    4. $[1, V] $ 的矩阵经过 Softmax 函数变换为概率矩阵 $\hat y$ ，其中数值最大的那个就代表预测出来的中间词 $v_{c}$ 的索引。
    5. 与真实的中间词 $v_{c}$ 的 one-hot 向量比较，计算误差。
  - 后向过程
    前向过程已经说明有了 $V$ 和 $U$ 向量，即权重矩阵 $W_{V*N}$ 和 $W'_{N*V}$ ，模型是如何训练的。后向过程则会说明如何优化参数 $V$ 和 $U$ 。
    1. 使用交叉熵作为损失函数：
      $\hat{y}, y) = - \sum_{j=1}^{V} y_{j}log(\hat{y_{j}})$
      $\hat{y_{j}}$ 的结果是经过 Softmax 计算后的一个概率向量， $y_{j}$ 则是一个 one-hot 向量。
    2. 最小化损失函数：
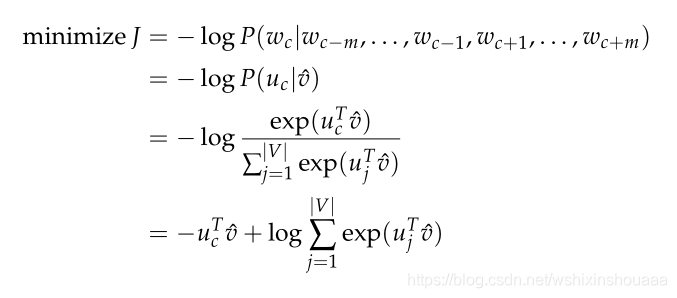
    3. 使用梯度优化算法更新所有的词向量 $u_{c}$ 和 $v_{j}$ 。

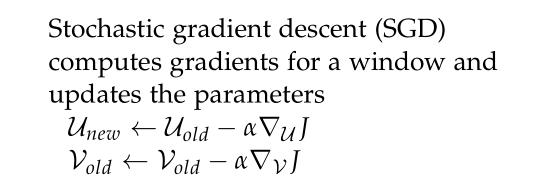
Two Training methods

Hierarchical softmax
- 原理
  1. 从隐藏层到输出层的 Softmax 时，需要计算 $\frac{exp(u_{o}^T v_{c})}{\sum_{w=1}^{\left| V \right|} exp(u_{o}^T v_{c})}$ ，然而分母里直接将中心词与所有词进行计算非常耗时，所以就引出了 层次softmax 。
  2. 根据单词的个数建立霍夫曼树，作为从隐藏层到实际单词的映射过程，取代了从隐藏层到输出层中 Softmax 的计算结果 $y^{'}$ 。
  3. 与霍夫曼树编码不同的是，往左时编码为 1，往右时辩吗为 0，刚好和霍夫曼树编码反过来。
  4. 每个叶子结点都是一个单词 $w $ ，叶子结点总数为词汇表的大小 $V $ 。
  5. 非叶子结点作为其左右子树中所有单词的集合，用符号 $\theta =n(w_{i},k)$ 表示， $k $ 表示该结点属于第几层， $\theta$ 是该结点的向量表示。
  6. 每一个非叶子结点都要进行一次二分类，既然是二分类，那就用 sigmoid 函数来进行判断。往右走的概率为： $\sigma(x_{w}, \theta) = \frac{1}{1 + exp(-x_{w}\theta)}$ ，往坐走的概率为： $\sigma(x_{w}, \theta)$ 。
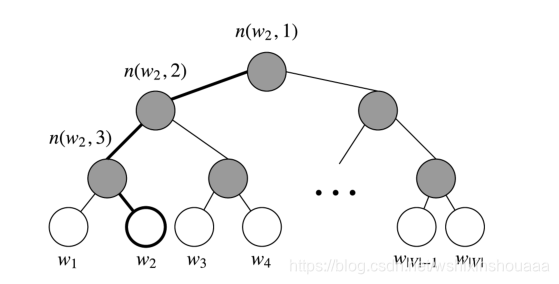
- 目标
  找到合适的词向量 $x_{w}$ 和结点 $\theta$ ，以找到词 $w_{2}$ 为例，最大化似然函数：
  $\prod_{i=1}^{3}P(n(w_{2}, i)) = [1-\sigma(x_{w_{2}},\theta_1)][1-\sigma(x_{w_{2}},\theta_2)]\sigma(x_{w_{2}},\theta_3) $
  所以，给定要寻找的某个输出词 $w$ 所经过的某个结点的概率可以定义为：
  $$P(d_i|x_w,\theta_{i-1})=
  \begin{cases}
  1 - \sigma(x_w \theta_{i-1}) & d_i=1
  \sigma(x_w \theta_{i-1}) & d_i=0\
  \end{cases}$$
  其中 $d_i \in \{0,1\}, i=2,3,L(w)$ 为霍夫曼编码， $i = 1$ 为根结点，$L(w) $ 为到词 $w$ 的路径中做包含的结点个数。
  那么，设对于要查找的某个输出词 $w $ 的概率，即最大似然函数为：
  $\prod_{i=2}^{L(w)} P(d_i|x_w,\theta_{i-1}) = \prod_{i=2}^{L(w)}[1-\sigma(x_w)\theta_{i-1}]^{d_{i}} [\sigma(x_w)\theta_{i-1}]^{1-d_{i}} $
  所以，最后的目标函数为负的对数似然函数
  $L(x_w, \theta_i) = log \prod_{i=2}^{L(w)} P(d_i|x_w,\theta_{i-1}) = \sum_{i=2}^{L(w)} d_i log [1-\sigma(x_w)\theta_{i-1}] + d_i log [\sigma(x_w)\theta_{i-1}] $
  将其最小化即可：
  $L(x_w, \theta_i)$
- 优点
  1. 计算量由 $V$ 变为 $log_{2} V$ 。
  2. 使用频率越高的词离根结点越近，查找时间越短。
Negative sampling
将其最小化即可：
$L(x_w, \theta_i)$
- 优点
  1. 计算量由 $V$ 变为 $log_{2} V$ 。
  2. 使用频率越高的词离根结点越近，查找时间越短。
Negative sampling

原文链接：https://blog.csdn.net/wshixinshouaaa/article/details/100499719

Word2Vec Tutorial

Idea

Two model

Skip-Gram(SG)

基本思想

模型

过程

参数

前向过程

后向过程

目标函数

推导过程

Continuous Bag of Words(CBOW)

基本思想

本质

模型

过程

前向过程

后向过程

Two Training methods

Hierarchical softmax

原理

目标

优点

Negative sampling

优点

Negative sampling