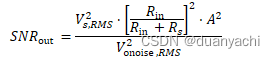- 概述
电噪声是一个电路中不需要的电流或电压信号。真正的信号是这种不需要的噪声和想要的信号之和。
噪声的类型包括:
1)由导线或器件中电荷的离散和随机运动产生的噪声(我们称之为固有的电路噪声,如热噪声、shot噪声或闪烁噪声);
2)量化噪声(将模拟信号变为数字信号时由有限的数字字大小产生);
3)耦合噪声(由相邻电路的信号相互馈入和干扰产生)。
本章中重点讨论固有噪声。
- 8.1信号
对于一个正弦信号
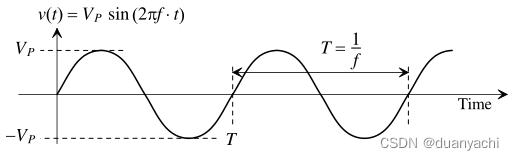
书上很有趣的比喻:
这个信号的平均值是零。这是否意味着,如果这个信号被施加在一个电阻上,平均功率的耗散为零?当然不是(否则许多人就不能做饭或取暖)。
电阻所耗散的瞬时功率(电阻在某一特定时间所耗散的功率t)写成
?inst ?=?2??=??2sin22?⋅???![]()
将这个功率在时间上相加,结果为
Energy =0∞??2sin22?⋅???⋅??
平均耗散的功率
Average power dissipated =1?0T??2???22?⋅???⋅??![]()
均方电压
Mean-squared voltage =?2=1?∫0???2sin22?⋅??⋅??=??22![]()
均方电压的平方根(其结果称为均方根,RMS)
2?2=????=21?∫0???2sin2(2??⋅?)⋅??=??22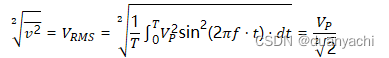
当VRMS=VDC时,正弦波或直流源的电阻耗散的功率是相同的。
计算多个正弦波电压叠加的电路时,一般通过对多个均方电压(而不是均方根电压)求和然后开根号除以总电阻获得电路总的均方根电压。而不是把你每个均方根电压求和。
- 8.2功率谱密度
频谱分析仪(SA)
频谱分析仪(SA)是一种评估信号的频谱内容的仪器。图8.4是频谱分析仪的框图。SA的输入被乘以一个正弦波的频率对输入信号进行移位。乘法后,带通滤波器将频率范围限制在fres的带宽内(测量的分辨率带宽)。然后测量带通滤波器的输出信号中的功率。计数指数n使测量从起始频率fstart到停止频率fstop变化。这个频率范围构成了我们频谱图的X轴
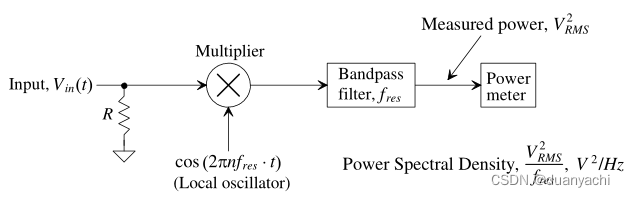
baker又开始举例子:假设我们想看一个从直流(f=0=fstart)到10kHz(=fstop)的信号的频谱,分辨率为100Hz(=fres)。假设我们想看的信号是一个1V的峰值振幅在4.05kHz的正弦波,与1V的直流电串联,???(?)=1+sin(2?⋅4.05kHz⋅?) V,计算指数n的范围,![]()
?stop =10kHz=?max⋅?res →?max=100。计数指数将从0到100变化。换句话说,图8.4中余弦信号的频率将从0到10kHz,以100Hz为单位变化。我们的图将有101个点。
应用我们的输入信号,测量第一点的功率,n=0(或者对于x轴f=0)。应用于乘法器的余弦项为1。整个输入信号被应用于带通滤波器。在一般的SA中,使用一个带通滤波器。在这个例子中,我们使用一个低通滤波器,因为DC<100Hz。施加在功率计的信号是(1V)2。对于这个位于f=0(和n=0)的第一点,y轴单位可以是峰值电压(=1 V)、均方(=1/2 V2)、有效值(=1/2V=VRMS)、功率(=1/2R=V2RMS/R W,其中R是图中看到的SA的输入2 VRMS 2 /R电阻。),功率谱密度(PSD)(= 1/[2Rfres],单位为W/Hz或Joules1),或电压谱密度(= VRMS /fres = 1/2·100 /fres )单位为W/??。
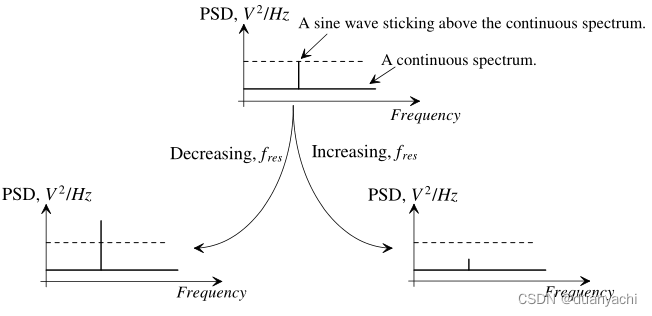
通常情况下,PSD的单位是V2/Hz。对于噪声来讲,我们在噪声分析中使用PSD(以及其他地方),因为对于一个连续的频谱(在这个例子中我们没有,但对于噪声信号来说是很常见的)。fres上升提高了我们测量的(V2RMS),导致V2RMS/fres是常数。所以连续频谱的PSD大小不随fres变化而变化。不幸的是,对于信号来讲,不幸的是,当测量一个单一的正弦波时,增加fres会降低正弦波的振幅PSD振幅,如图所示
继续我们的测量,当n=1,乘法器频率为100Hz时,乘法器的输出是
cos(2?⋅100⋅?)⋅(1+sin[2?⋅4.05kHz⋅?]) volts;cos?⋅sin?=12(sin[?−?]+sin[?+?])![]()
cos(2?⋅100?)+12(sin[2?(3.95?)?]+sin[2?(4.15?)?]) volts![]()
这个乘法器的输出信号(记住n=1)包含三个频率为100 Hz、3.95 kHz和4.15 kHz的正弦波。将这个信号通过滤波器,允许从直流到<100赫兹的频率通过,结果是测量功率为零。
这假定了一个理想的滤波器不会通过100赫兹(见本节末尾的评论)。事实上,很容易表明,在.nfres =4 kHz之前,我们得到的测量信号为零 当本地振荡器频率为4 kHz时,乘法器的输出为
cos(2?⋅4??)+12(sin[2?(50)?]+sin[2?(8.05?)?]) volts![]()
也就是一个包含50Hz、4kHz和8.05kHz频率的功率的信号。同样,滤波器将范围内的信号内容传递给功率计。0 f 100 Hz 从滤波器出来的是50 Hz的正弦波,峰值振幅为0.5 V。下一个测量点发生在 。应用于滤波器的信号(乘法器的4.1kHz输出)
cos(2?⋅4.1??)+12(sin[2?(−50)?]+sin[2?(8.15?)?])![]()
这里出现的负频率信号可以被认为是一个相移的正频率信号。因为正弦函数是一个奇数函数,sin(- 2π f ·t)=-sin( 2π f ·t)=-sin( 2π f ·t±π),在50赫兹仍有频谱内容。施加在仪表上的信号是50 Hz的正弦波,振幅为0.5 V。输入的4.05kHz分量的总(测量)信号振幅是4kHz和4.1kHz时测量的信号振幅之和(即1V之和)。当绘制nfres点时,测量的相邻点的振幅被相加。例如,当nfres为4kHz和4.1kHz时,我们可以在4.05kHz绘制一个振幅为1V的点,将测量的信号相加。我们可以在3.95和4.15kHz的位置上绘制出振幅为0.5V的点,因为在3.9kHz和4.2kHz,我们的测量信号为零。
- 8.2线路噪声
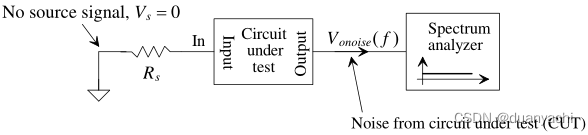
如图所示,从一个电路中出来的电噪声可以用SA来测量。8.6. 被测电路(CUT)被连接到频谱分析仪上,没有施加源信号,也就是说,输入端接地或终止于一个电阻,如50Ω。如果从CUT出来的噪声低于SA的本底噪声,则在CUT和SA之间插入一个低噪声放大器(LNA),以帮助噪声测量(然后测量的噪声由LNA的增益增加)。如上一节所述,我们通常绘制PSD与频率的关系,以最终描述信号的功率或信号的有效值。
- 8.2.1电路噪声的计算和建模
- 图8.7显示了一个噪声信号的时域表示。如果这个噪声信号的PSD被称为 ,我们可以用以下方法确定其有效值
????=∫?????noise 2(?)⋅?? Volts![]()
其中fL和fH是感兴趣的最低和最高频率。如果噪声PSD是平坦的(通常被称为 "白噪声频谱",因为白光包含所有可见波长的光谱内容),那么这个方程就简化为
????=??−??⋅?noise 2(?)=?⋅?noise 2(?)![]()
其中,测量的带宽,B,是fH fL。
输入-延迟噪声 I
噪声是在电路的输出上测量的。然而,它可以返回到电路的输入端,与输入信号进行比较。这种输入参考噪声并不真正存在于CUT的输入上。这对于CMOS电路尤其如此,CUT的输入可能是MOSFET的多晶硅栅极。虽然直接隧道门电流噪声可能存在,但它通常比平均(直流)隧道门电流要小得多,通常对测量的输出噪声贡献很小。
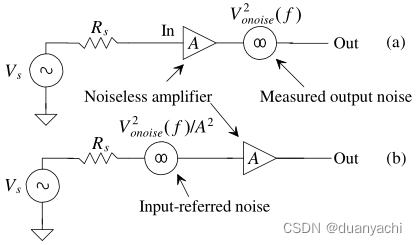
考虑一下图8.8中看到的放大器模型。图8.8a显示了测量的输出噪声PSD。我们可以计算输入参考PSD,图8.8b,简单地用输出PSD除以放大器的增益A的平方(或用电压谱密度=PSD,除以增益)。
噪声等效带宽
图 8.9a 显示了一个白噪声频谱。如果我们要从这个频谱计算噪声电压的 RMS 值,在无限带宽上,我们最终会得到一个无限 RMS 噪声电压。在实际电路中,信号和噪声是有带宽限制的(它们的频谱内容在某些频率下为零)。这种带宽限制可能是电路中有意添加或存在寄生电容的结果。
如果我们假设 CUT 具有单极衰减,如图 8.9b 所示,并且 CUT 的低频噪声是白噪声(再次如图 8.9b 所示),那么我们可以计算RMS 输出噪声使用
?onoise ,???2=∫0∞???, noise 21+???3??22?? ∫???2+?2=1?tan−1??+?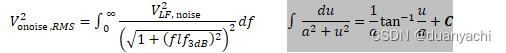
?onoise ,???2=???, noise 2⋅?3??⋅tan−1???3??0∞
=???, noise 2⋅?3??⋅?2???
其中 NEB 是噪声等效带宽
?onoise ,???=???⋅???, noise 2![]()
当然,这假设在频率接近 f3dB 之前是恒定的。
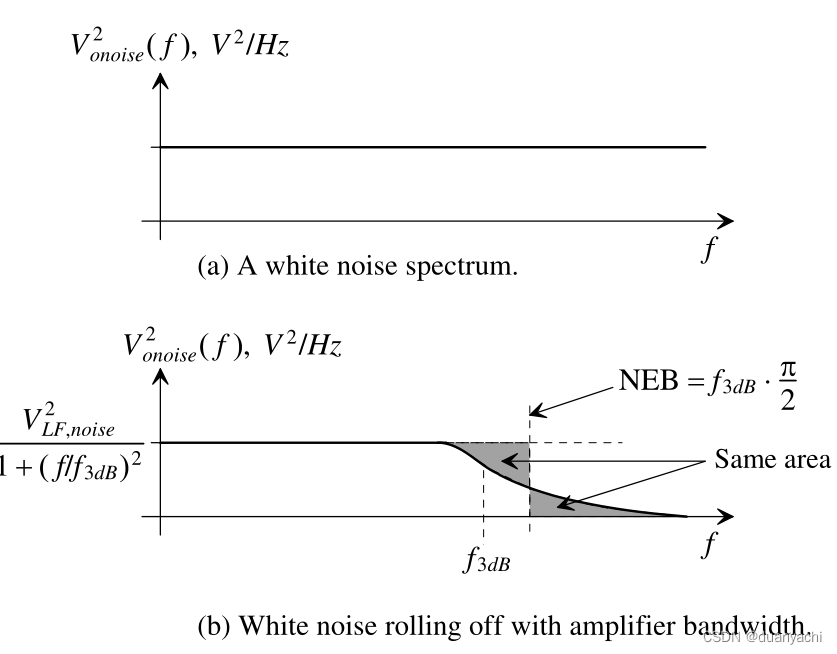
图 8.9b
在实践中,噪声的频率响应可能会跟随(与)放大器的频率响应相关。如果是这种情况,我们可以将放大器的频率响应写成
?(?)=?????in =???1+???3??=1001+???3??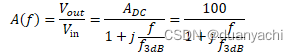
其中 f3dB = 1 MHz。我们可以使用以下方法确定输入参考噪声 PSD
?inoise 2(?)=?onoise 2(?)|?(?)|2=???, noise 21+?∣?3??2⋅1+?∣?3??2???2=???, noise 2???2![]()
显示输出噪声的输入参考 PSD 是从 DC 到无穷大的平坦频谱
这样做的问题是,如果为了确定 RMS 输入参考噪声,我们将这个 PSD 在无限带宽上积分,我们会得到无限 RMS 电压。我们必须记住,输入参考噪声用于对电路的输出噪声进行建模(有明显限制)(同样,您无法测量输入参考噪声,因为它并不真的存在!)。
输入参考噪声仅用于了解电路如何破坏输入信号。后一点很重要,因为具有相同带宽的两个放大器可能具有相同的输出噪声 PSD,但增益不同。具有较大增益的放大器将具有较小的输入参考噪声,从而产生具有更好信噪比的输出信号。知道输出噪声是带限的,并且输入参考 RMS 电压应该反映这一点,我们可以写
?inoise ,???=???⋅???, noise 2???=?onoise ,??????![]()
级联放大器中的输入参考噪声
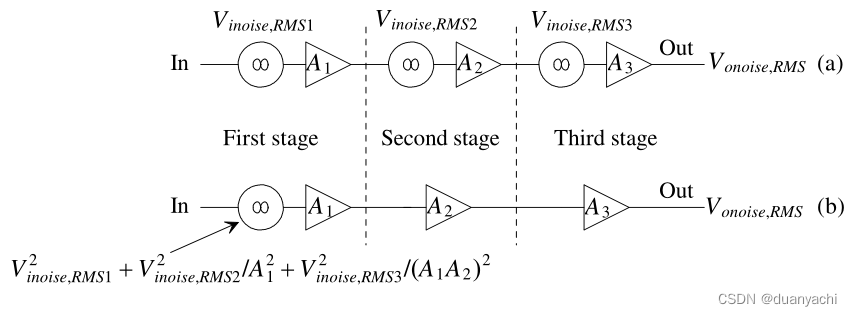
图 8.11a 显示了具有相应输入参考噪声源的噪声放大器级联。 (a) 中的输出噪声功率可以写成
![]()
再次记住我们添加了每个放大器的噪声功率。 (b) 中的输入参考噪声由下式给出
![]()
这里要注意的关键点是,第一个放大器的噪声对放大器链的噪声性能影响最大。为了获得良好的噪声性能,第一级的设计至关重要。
例 8.3 评论方程的局限性。 (8.21) 和 (8.22) 用于计算噪声。
测量的输出噪声通常包括源电阻的热噪声。如果在我们级联放大器时有效源电阻发生变化,则为输入参考噪声计算的值 Vinoise,RMS 也会发生变化。一个可能更重要的问题是噪声带宽的变化。
级联放大器会降低电路的带宽。方程的点。 (8.21) 和 (8.22) 仍然有效,即第一级的输出噪声和增益(相当于说“输入参考噪声”)对于整体低噪声性能至关重要。但是,要准确确定输入参考噪声,最好测量级联输出上的噪声,然后将其返回到级联输入。冒着明显的风险,级联放大器的增益是通过在放大器的通带内(不太高或太低)的频率向级联输入应用一个小的正弦波信号来确定的。将级联的输出正弦波幅度与输入正弦波幅度之比称为增益。然后,输入参考噪声是输出 RMS 噪声除以整个级联的增益。
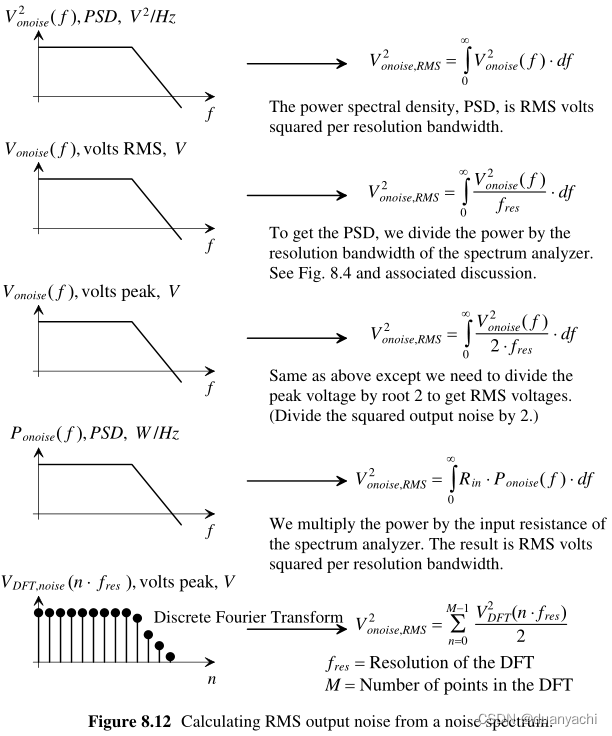
- 8.2.2热噪声
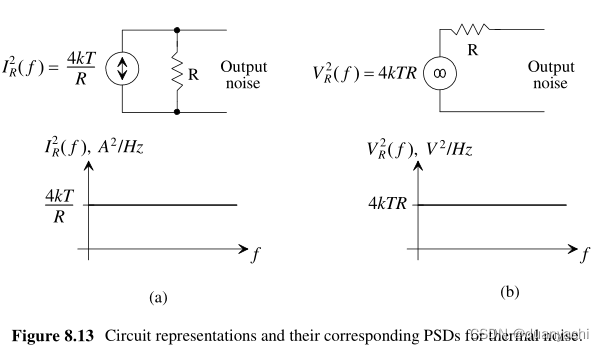
电阻器中的噪声主要是由于热效应引起的电子随机运动的结果。这种类型的噪声被称为热噪声、约翰逊噪声、奈奎斯特噪声(在 John B. Johnson 或 Harry Nyquist 之后,Johnson 第一次观察到这种效应并且奈奎斯特解释了它)或 Johnson-Nyquist 噪声。电阻器中的热噪声可以通过 PSD 来表征
??2(?)=4??? with units of V2/Hz(注意热噪声是白色的并且与频率无关)其中k = Boltzmann’s constant = 13.8 x 10–24 Watt ·sec/° K (or J/° K)T = temperature in °KR = resistance in![]()
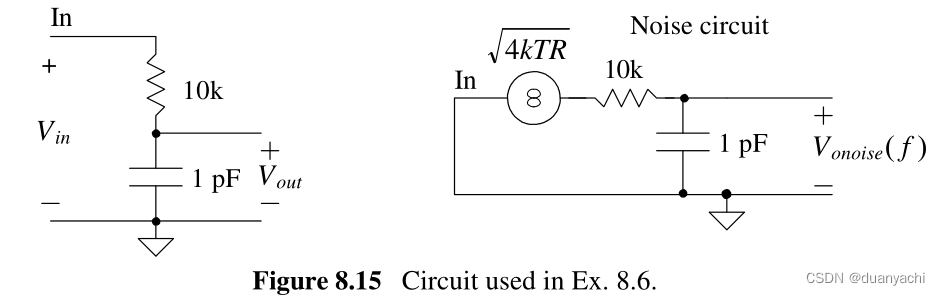
该电路中唯一产生噪声的元件是电阻器。它会产生热噪声。电阻器的噪声电压谱密度为 。4ktr 噪声谱密度为![]()
?onoise (?)=4???1/???1/???+?=4???1+???3?? units, ?/??![]()
?onoise 2?=4???1+???3??2=4???1+???3??22=4???1+???3??2 ?3??=1/2???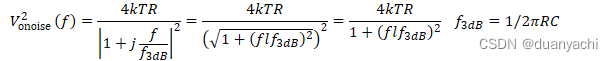
这种单极衰减是我们之前讨论的 噪声等效带宽 (NEB) 的原因,例如。 8.2.使用方程式。 (8.17),输出RMS噪声电压为
?onoise ,???=12???⋅?2⋅4???=???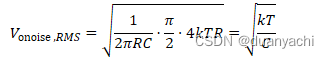
- 8.3.2信噪比
信噪比 (SNR) 可以通过以下一般术语定义:
???= desired signal power, ?? undesired signal power (noise), ?noise ![]()
SNR 可以使用 dB 指定为
???=10log???noise ![]()
如果功率归一化为 1-负载(例如 ),我们可以写
???=10log???noise =20log???noise =20log??,????noise ,???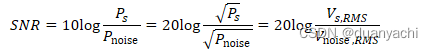
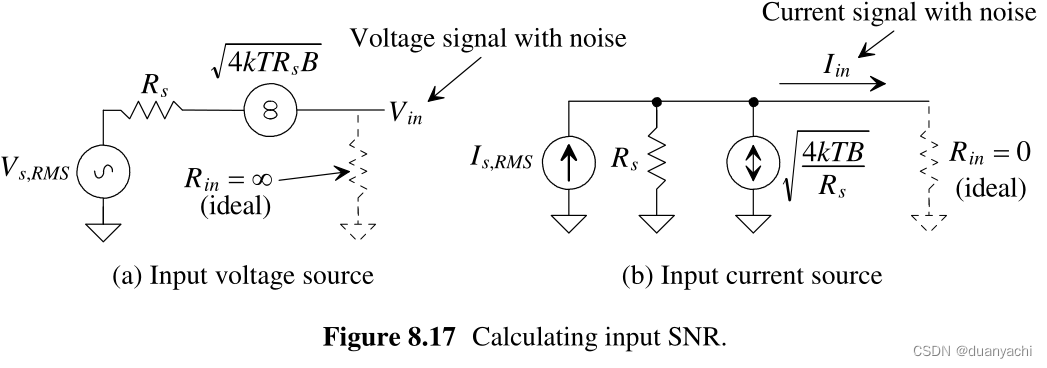
图 8.17 显示了两个具有相关热噪声模型的等效输入源。对于理想的 Rin,与这些电路相关的 SNR 是(注意 Vs,RMS 2 )开路(电压输入)或短路(电流输入)
?????=??,???24?????=??,???24???/??![]()
在图 8.17a 中,Vin 通过无限 Rin(开路)下降。在图 8.17b 中,Iin 驱动零 Rin(短路)。在实际情况下,Rin 是有限且非零的。对于图 8.17a,输入信号和噪声由 Rs 和 Rin 之间形成的分压器衰减
?????=??,???2⋅????in +??24?????⋅??????+??2=??,???24?????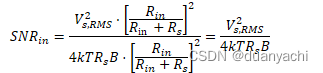
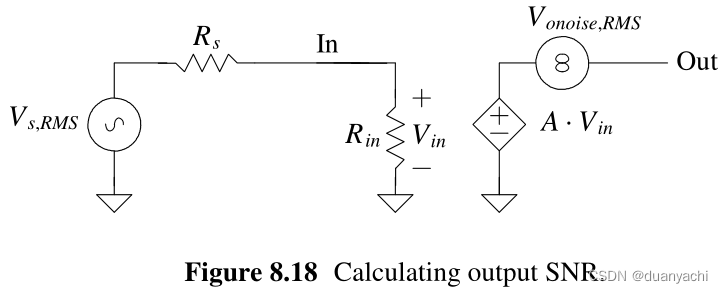
检查带有噪声的放大器模型,如图 8.18 所示。输出噪声 Vonoise,RMS 包括来自 Rs 的热噪声贡献。我们在源连接到放大器的情况下测量了输出噪声(见图 8.6 和 8.8)。然后,与放大器输出相关的 SNR(其中噪声由放大器引起,而来自 Rs 的热噪声)为
???out =??,???2⋅?in ?in +??2⋅?2?onoise ,???2