之前看过高斯过程(GP)，不过当时也没太看懂，最近花时间认真研究了一下，感觉总算是明白咋回事了，本文基于回归问题解释GP模型的思想和方法。文中的想法是自己思考总结得来，并不一定准确，也可能存在错误性。
为什么要用GP？
回顾一下我们之前在解决回归问题时，就拿线性回归举例，我们为了学习映射函数，总是把函数参数化，例如假设
，然后计算参数
的后验分布，把参数估计出来之后，就得到了我们想要学习的函数，接着就可以用这个函数去做预测了。
但是有时候我们并不知道数据到底用什么形式的函数去拟合比较好(是1次的，2次的还是10次的？)。这个时候高斯过程(GP)就闪亮登场了，GP说：“我不需要用参数去刻画函数，你就告诉我训练数据是什么，你想要预测哪些数据，我就能给你预测出结果。“这样一来，我们就省去了去选择刻画函数参数的这样一个过程。
GP是怎么来的？
那么GP是怎么做到的呢？我们先来看这样一件有趣的事情：
假设我们的函数定义域和值域都是
,那么如果你的训练集是包含了所有定义域的，那么这个函数
我们就得到了，你给任何一个点，我都能通过查表的方式告诉你结果是多少。第二种情况我们的训练集中缺少了
这四个点，并且这四个点就是我们需要进行预测的点，如果我们可以通过某种方式建立一个4维的概率分布
，其中
分别代表
的预测值，那么我们是不是就可以就可以利用这个概率分布，找到对应的概率最高的点把最终的结果给估计出来。
然而，事实上虽然很多实际问题（比如房价的预测），它的定义域和值域都是
(或者是某个连续的区间)，但是我们的训练数据是有限的，而基于这些训练数据，我们要对整个实数域进行预测，如果我们继续利用上面的思想的话，我们需要建立一个无穷维度的概率分布（因为我们需要进行预测的数据点事无穷个的），这显然不可能，不过庆幸的是，在每一次我们需要进行预测的时候，我们所需要进行预测的数据是有限的。假设有N个训练数据
,有N*个需要进行预测的数据
,
表示
，那么我们最终其实就是希望得到
(
代表了
所有预测值的变量的集合)。
高斯过程(GP)
下面我们就开始正式的介绍高斯过程(GP)，它是怎么得到这个
，然后去做预测的。在GP中，首先基于训练数据和测试数据，定义了基于定义域
的函数的概率分布
其中
。
是正定的核函数。
代表了
所有预测值的变量的集合。这里有一个关键的思想，如果核函数认为两个输入是非常相似的，那么函数给出的输出值也会非常的相似。(在这样的刻画中，我们发现
其实好像并没有太大的作用，事实上，我们通常令
)。这个定义总体给出了三个信息：
- 在本次训练中，我们的定义域是
。
- 在这个定义域中，如果
基于核函数是非常接近的，那么你们的输出值也会非常接近。
- 我们是用高斯分布去进行刻画（用高斯的好处，至少有一点条件概率密度函数很好算）。
我们把上面的概率分布展开：
其中
利用高斯分布的性质（通过联合分布计算条件分布），我们可以得到
这样我们计算出了我们希望得到的
。至此为止，整个GP就结束了。关于GP那么它有什么优点呢，我认为有两点：
- 这一点也是我们上面就说过的，GP是无参的，对于任何一组数据，你不需要知道他的结构是什么，你也不需要去用参数刻画它函数的样子，GP就可以帮你做预测。
- GP它刻画出了函数的概率分布。这个非常有用。回顾之前的线性回归的方法，当你把参数
估计出来后，你的函数就确定了，接下来我拿出任何一个数，你都会“毫无感情的”给我一个预测值。但是GP不一样，当我们知道我们预测函数的不确定度（不确定度很高，这个预测的结果就不可靠）之后，我们能探索最不可能实现高效训练的数据区域。这也是贝叶斯优化背后的主要思想。下面这句话我觉得写得非常贴切：如果你给我几张猫和狗的图片，要我对一张新的猫咪照片分类，我可以
有噪声观测的情况下
在有噪观测的情况下，我们假设观测模型是这样的
，其中
，那么观测的核函数则更新为
（假设不同观测之间是独立的），基于这样的假设，联合概率分布和条件概率分布分别是：
，
核函数参数的影响
那么核函数对GP有什么影响呢，假设我们选择SE核函数：
（
表示p=q时取1，否则取0）
这个核函数有三个参数，分别是
，
和
，分别控制着水平尺度，垂直尺度，以及噪声的方差。通过三幅图我们来看看这三个参数是怎么控制预测的结果的：
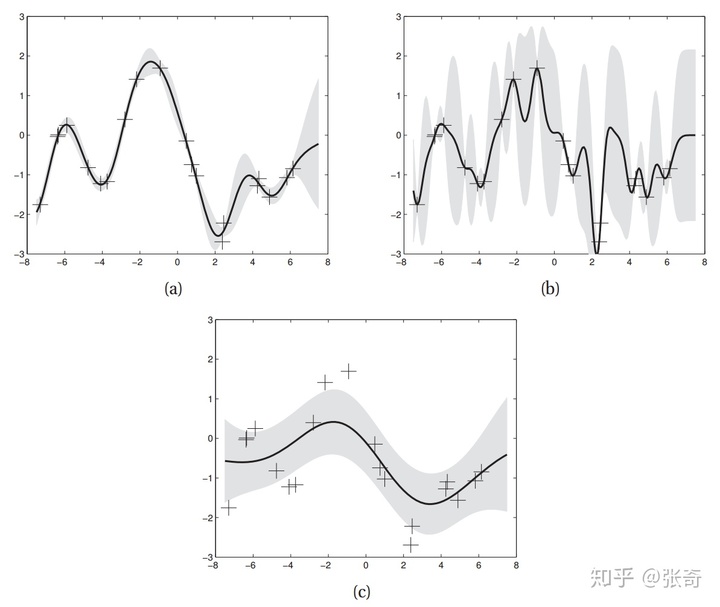
三幅图的超参数
分别是：
。（只改变
，其他的参数是通过优化边际似然函数得到的）
我们可以看到（a）图整体看上去是估计的比较好的，（b）图中，减小了
,我们发现图变得弯弯曲曲的，而且一旦预测的数据点稍微远离训练的数据点，这个不确定度就大大的上升（因为只要输入的距离稍微大一点点，核函数就认为它们已经非常不相似了）。（c）图中，
为3，函数看上去更加的平滑了，但是拟合的效果就显得很差。
