深度学习中的梯度消失与梯度爆炸及解决方案

1.梯度消失与梯度爆炸

反向传播算法在神经网络中非常常见，可以说是整个深度学习的基石。在反向传播中，经常会出现梯度消失与梯度爆炸的问题。梯度消失产生的原因一般有两种情况：一是结构较深的网络，二是采用了不太合适的激活函数。而梯度爆炸一般也有两种情况：一是结构较深的网络，二是初始化权重不合适，权重值太大。

从网上找了一张深度网络示例图，简单说明一下梯度消失或者爆炸的问题。

其中${\sigma }^{\prime }(z_4)$表示激活层的导数，$w_4$是该层的权重。${\sigma }^{\prime }(z_4)w_4$这部分如果大于1，那么层数增多的时候，最终的梯度会以指数方式增加，这个时候会发生梯度爆炸。而如果这部分小于1，那么层数增多的时候，最终的梯度会以指数的形式衰减，这个时候就会发生梯度消失。

2.梯度消失/爆炸的解决方案

2.1 梯度裁剪

梯度裁剪主要是针对梯度爆炸提出。其思想也比较简单，训练时候设置一个阈值，梯度更新的时候，如果梯度超过阈值，那么就将梯度强制限制在该范围内，这时可以防止梯度爆炸。
权重正则化（weithts regularization)也可以解决梯度爆炸的问题，其思想就是我们常见的正则方式。

$$Loss=(y-w^{T}x{)}^2+\alpha ||w|{|}^2$$

$\alpha$是正则化系数。如果发生梯度爆炸，||w||的平方会变得非常大，这样就可以一定程度避免梯度爆照。

2.2.relu等激活函数

relu我们就非常常见了，在AlexNet网络中最先提出。relu激活函数的导数为1，那么就不存在梯度消失爆炸的问题，不同层之间的梯度基本保持一致。
而relu的缺点则是，负数部分恒为0，所以存在一定‘死区’，会导致一些神经元无法被激活，可以通过elu等来改善死区的问题。

2.3.batch normalization

batch normalization目前已经被广泛的应用到了各大网络中，具有加速网络收敛速度，提升训练稳定性的效果.BN本质上是解决反向传播过程中的梯度问题，通过规范化操作将输出信号x规范化到均值为0，方差为1保证网络的稳定性。

在我们前面推导的反向传播求导公式中，含有$w$项，所以w的大小影响了梯度的消失和爆炸。BN就是通过对每一层的输出规范为均值和方差一致的方法，消除了w带来的放大缩小的影响，进而解决梯度消失和爆炸的问题。

2.4 ResNet 残差结构

Residual Net中包含残差的shortcut(捷径)部分，shortcut的网络结构为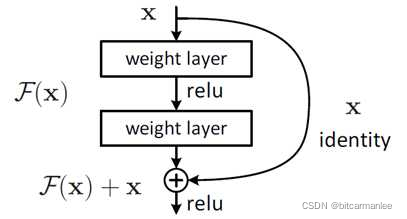

残差网络主要是为了解决梯度消失的问题。从上面的网络结构可以看出，由于shortcut的存在，残差网络的输出在对于输入求导时，总有一个x保证有一个常数梯度1(除非F(X)刚好求导为-1这样导数求和为0，但这种概率太小)，所以一定程度能解决梯度消失的问题。如果从输入到输出，恒等映射是最优解，那么将残差F(x)直接设置为0即可。