语音识别——语言模型

本博客主要是摘写洪青阳教授的《语言识别-原理与应用》的笔记，不足之处还请谅解。

语音识别为：根据输入的观察值序列O，找到最可能的词序列 $\hat{W}$ 。按照贝叶斯准则，识别任务可做如下转化：
$\hat{W}= {\underset {W}{\operatorname {arg max} }}\,P(W|O)=\arg\,\max\frac{P(W)P(O|W)}{P(O)}$
其中， $P (O)$ 和识别结果 $W$ 无关，可忽略不急，因此 $\hat{W}$ 的求解可进一步简化为：
$\hat{W}={\underset {W}{\operatorname{arg\,max}}}\,P(W)P(O|W)$
要找到最可能的词序列，必须使上式右侧两项的乘积最大。其中， $P (O ∣ W)$ 由声学模型决定， $P (W)$ 由语言模型决定。

声学模型就是前面学过的，通过声音进行分析的模型。

语言模型用来表示词序列出现的可能性，用文本数据训练而成，是语音识别系统重要的组成部分，如下图所示。

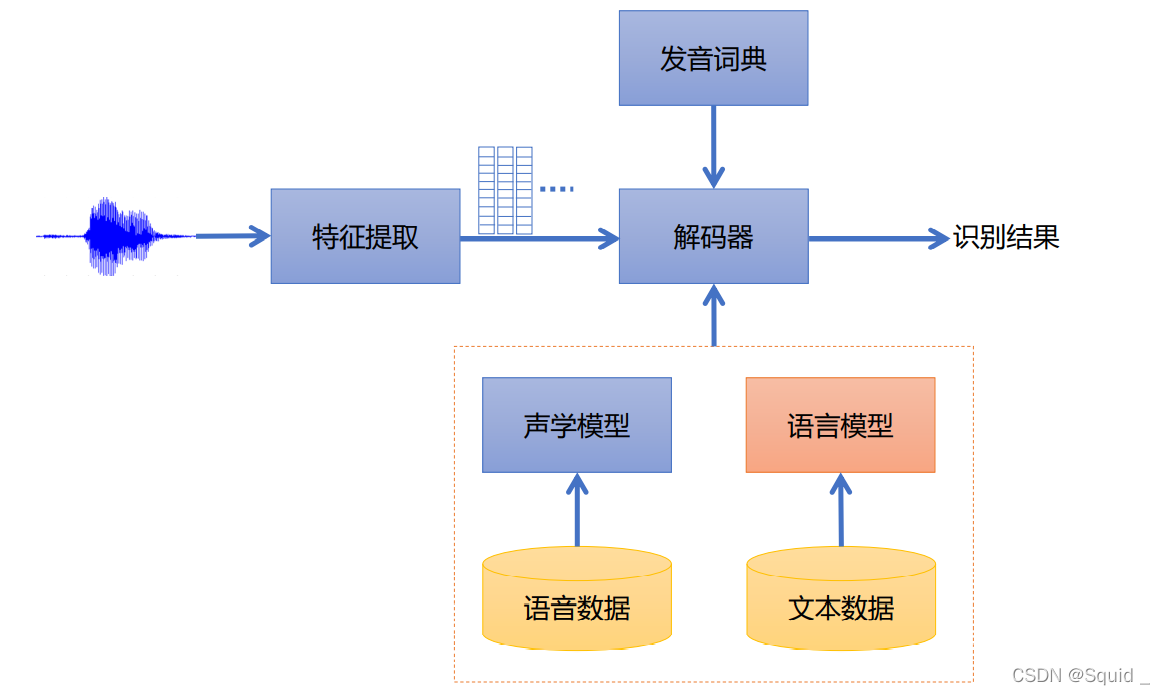
请添加图片描述

上图即为我们熟知的语音识别框架。

语言模型用来表示词语序列出现的可能性，可以基于语法规则，也可以基于统计方法。

基于规则的语言模型：来源于语言学家掌握的语言学知识和领域知识，或者根据特定应用设定语法规则，一般仅能约束受限领域内的句子。

统计语言模型：通过对大量文本语料进行处理，获取给定词序列的概率分布，从而能够客观描述隐含的规律，适合于处理大规模真实文本。统计语言模型已被广泛应用于语音识别、机器翻译、文本校对等多个领域。

而要训练一个适用性强的统计语言模型，就需要大量的、不同的、能覆盖用户各种表达方式的文本语料。

请添加图片描述

所有的句子都有开始位置和结束位置，分别用<s>和</s>表示，可认为这两个特殊标记是两个词。语言模型刻画词与词之间的组合可能性，通过分词，将句子进一步转换为词与词之间的组合概率关系。

即统计语言模型的目标是计算出给定词序列 $w_1,\cdots,w_{t-1},w_t$ 的组合概率：
$P(W)=P(w_1w_2\cdots w_{t-1}w_t)\\ =P(w_1)P(w_2|w_1)P(w_3|w_1w_2)\cdots P(w_t|w_1w_2\cdots w_{t-1})$
其中，条件概率 $P(w_1),P(w_2|w_1),P(w_3|w_1w_2),\cdots,P(w_t|w_1w_2\cdots w_{t-1})$ 就是语言模型。

计算所有这些概率值的复杂度较高，特别是长句子的计算量很大，因此需做简化，一般采用最多n个词组合的n-gram模型。

n-gram模型

所谓n-gram模型，表示n个词之间的组合概率模型。在n-gram模型中，每个预测变量 $w_t$ 之与长度为n-1的上下文：
$P(w_t|w_1\cdots w_{t-1})=P(w_t|w_{t-n+1}w_{t-n+2}\cdots w_{t-1})$
即n-gram预测的词概率值依赖于前n-1个词，更长距离的上下文依赖被忽略。考虑到计算代价，在实际应用中一般取 $1\leq n \leq 5$ 。

当n=1,2和3时，相应的模型分别成为一元模型、二元模型和三元模型。

一元模型和多元模型有明显的区别，一元模型没有引入“语境”，对句子的约束最小，其中的竞争最多。而多元模型对句子有更好的约束能力，解码效果更好。

但相应地，n越大，语言模型就越大，解码速度也越慢。

而语言模型的概率均从大量文本语料估计得到。针对一元模型，可简单地计算词的出现次数。

假设有1000个句子，其中：

“我们”出现100次，“明年”出现30次，“日子”出现10次，······
总共有21000个词标签，其中包括1000个结束符</s>

请添加图片描述

一元模型的计算如下：

P(“我们”) = 100/21000
P(“明年”) = 30/21000
P(“日子”) = 10/21000
P(</s>) = 1000/21000

一元模型的示意图如下：

请添加图片描述

而二元模型的计算如下。假设这1000句语料中出现下面两个词的组合情况如下：

10句以“我们”开头，5句以“明天”开头，……
2句以“日子”结尾，……
1次出现“我们明年”，3次出现“我们彼此”，……

则二元模型计算如下：

P(“我们”|) = 10/1000
P(“明天”|) = 5/1000
P(</s>| “日子”) = 2/10 ，“日子”出现10次
P(“明年”|“我们”) = 1/100 ，“我们”出现100次
P(“彼此”|“我们”) = 3/100

得到下表：

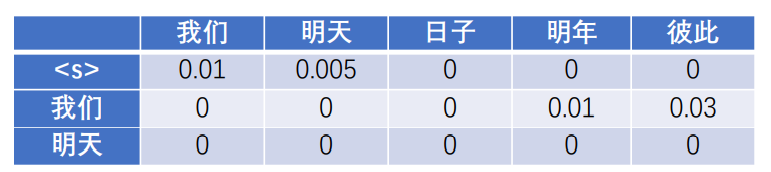
请添加图片描述

所以，二元模型的组合图如下：

请添加图片描述

三元模型用来表示前后三个词之间的组合可能性，其概率计算公式为
$P(w_3|w_1w_2)=count(w_1w_2w_3)/count(w_1w_2)$
假设“我们明天”出现2次，“我们明天开始”出现1次，则
$P (开始 ∣ 我们明天) = 1 / 2$
当句子只有一个词，例如”是“，其实也表示三个词，即”<s>是</s>“，因此要单独识别"是"，也得有这样一个词的句子。

三元模型的概率关系图如下：

请添加图片描述

评价指标——困惑度

给定句子S,其包含词序列 $w_1,w_2,\cdots,w_T$ ，T是句子长度，则困惑度（Perplexity）表示为：
$PPL(W)=P(w_1w_2\cdots w_T)^{-\frac{1}{T}}=\sqrt[T]{\frac{1}{P(w_1w_2\cdots w_T)}}$
Perplexity又称困惑度(PPL)， PPL越小，?(??) 则越大，句子?出现的概率就越高。

理论上，困惑度越小，语言模型越好，预测能力越强。

请添加图片描述

平滑技术

由于统计语料有限，会存在数据稀疏的情况，这可能导致零概率或估计不准的问题，因此对语料中未出现或少量出现的词序列，需要采用平滑技术进行简介预测。

平滑技术分为三种：

折扣法：从已有观察值概率调配一些给未观察值概率，如Good-Turing（古德-图灵）折扣法
插值法：将高阶模型和低阶模型做线性组合，如Jelinek-Mercer插值法，也可做非线性组合，如Kneser-Ney插值法。
回退法：基于低阶模型估计未观察到的高阶模型，例如Katz回退法。

Good-Turing折扣法

设总词数为 $N$ ，平滑前出现1次的词数为 $N_1$ ，出现 $c$ 次的词数为 $N_c$ 。
平滑后，概率 $P^*(出现0次的词)=\frac{N_1}{N}$ ，出现次数 $c^*=\frac{(c+1)N_{c+1}}{N_c}$ ，对应概率为： $P_{GT}=\frac{c^*}{N}$ 。

例子：

分词后句子语料（假设只有2句）：

“我们明年会有全新的开始”
“我们彼此祝福着等待再见那一天”

词频数：“我们”2次，“明年”1次，……，“天”1次

平滑前： $N = 16, N_1 = 14 , N_2 = 1$

平滑后： $N^*_0=\frac{N_1}{N}=\frac{14}{16},N^*_1=\frac{(1+1)N_2}{N_1}=\frac{2}{14}$
对应的概率为： $P^*_0=\frac{N_1}{N}=\frac{14}{16},P^*_1=\frac{c^*_1}{N}=\frac{2}{14*16}$

Jelinek-Mercer插值法

为了避免出现 $P (w) = 0$ 或接近于零的情况，可以用三元、二元和一元相对概率做插值。
$\hat{P}(w_t|w_{t-2}w_{t-1})=\lambda_1P(w_t|w_{t-2}w_{t-1})+\lambda_2P(w_t|w_{t-1})+\lambda_3P(w_t)$
其中 $\lambda_1+\lambda_2+\lambda_3=1$ 。

Kneser-Ney插值法

当训练数据非常少的情况下，特别适合采用Kneser-Ney 插值法。Kneser-Ney 是一种非线性插值法，从Absolute discounting（绝对折扣）插值方法演变而来。

Absolute discounting

Absolute discounting方法充分利用高阶和低阶语言模型，把高阶的概率信息分配给低阶的一元模型。例如，针对二元语言模型，Absolute discounting平滑公式表示如下：
$P_{abs}(w_t|w_{t-1})=\frac{max(c(w_{t-1}w_t)-d,0)}{\sum_{w'}c(w_{t-1}w')}+\lambda P_{abs}(w_t)$
其中 $c(w_{t-1}w')$ 表示 $w_{t-1}w'$ 的组合次数， $w^{'}$ 是任意一个词， $d$ 是固定的一个折扣值， $\lambda$ 是一个规整容量。 $P_{abs}(w_t)$ 是一元模型，按单词出现次数统计。

但 $P_{abs}(w_t)$ 可能会存在异常偏大现象。比如“杯子”出现频次较高，因此单独的“杯子”按出现次数可能会比 “茶”多，即 $P_{abs}(杯子) > P_{abs}(茶)$ ，这样会使Absolute discounting平滑公式因 $P_{abs}(w_t)$ 值过大出现“喝杯子”比“喝茶”概率高的奇怪现象。

Kneser-Ney

Kneser-Ney插值法对此做了改进，平滑公式如下：
$P_{KN}(w_t|w_{t-1})=\frac{max(c(w_{t-1}w_t)-d,0)}{\sum_{w'}c(w_{t-1}w')}+\lambda\frac{|\{w_{t-1}:c(w_{t-1},w_t)>0\}|}{|\{w_{j-1}:c(w_{j-1},w_j)>0\}|}$
其中 $\lambda$ 是规整的常量， $d$ 是固定的一个折扣值， $w_{j-1}w_j$ 是任意两个词的组合。第一部分的分母可进一步表示为一元模型统计，因此Kneser-Ney 平滑公式还可简化为：
$P_{KN}(w_t|w_{t-1})=\frac{max(c(w_{t-1}w_t)-d,0)}{c(w_{t-1})}+\lambda\frac{|\{w_{t-1}:c(w_{t-1},w_t)>0\}|}{|\{w_{j-1}:c(w_{j-1},w_j)>0\}|}$

Katz回退法

采用Katz平滑技术的概率估计公式如下：
$P(w_t|w_{t-2}w_{t-1})= \begin{cases} \frac{C(w_{t-2}w_{t-1}w_t)}{C(w_{t-2}w_{t-1})}, &当C>C'\\ d\frac{C(w_{t-2}w_{t-1}w_t)}{C(w_{t-2}w_{t-1})}, &当0<C<C'\\ backoff(w_{t-2}w_{t-1})P(w_t|w_{t-1}) \end{cases}$
其中 $C$ 是 $C(w_{t-2}w_{t-1}w_t)$ 的简写，表示三个词同时出现的次数， $C^{'}$ 是一个计数阈值，当 $C > C^{'}$ 时，直接采用最大似然方法估计概率；当 $0 < C < C^{'}$ 时，则采用Good-Turing折扣法， $d$ 是折扣系数。

$backoff(w_{t-2}w_{t-1})$ 是回退权重，回退权重的计算如下：
$backoff(w_{t-2}w_{t-1})=\frac{1-\sum{P(w|w_{t-2}w_{t-1})}}{\sum{P(w'|w_{t-2}w_{t-1})}}$
其中 $w$ 是在训练语料中 $w_{t-2}w_{t-1}$ 之后出现的词， $w^{'}$ 是在训练语料中 $w_{t-2}w_{t-1}$ 之后未出现的词。