Github链接
回顾前深度学习时代的推荐模型仍是非常必要的，因为：

1. 协同过滤、逻辑回归、因子分解机等传统推荐模型仍然凭借其可解释性强、硬件环境要求低、易于快速训练和部署等不可替代的优势，拥有大量适用的应用场景。
2. 传统推荐模型是深度学习推荐模型的基础

1 传统推荐模型的演化关系

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Cxq2rPYT-1653567457047)(https://raw.githubusercontent.com/SNIKCHS/MDImage/main/img/traditional_recsys_model_evolution.png)]

传统推荐模型的发展脉络主要由以下几部分组成。

(1) 协同过滤算法族

经典的协同过滤算法曾是推荐系统的首选模型，从物品相似度和用户相似度角度出发，分为物品协同过滤(ltemCF)和用户协同过滤(UserCF) 。为了使协同过滤能够更好地处理稀疏共现矩阵问题、增强模型的泛化能力，从协同过滤衍生出矩阵分解模型（ Matrix Factorization, MF ），并发展出矩阵分解的各分支模型。

(2) 逻辑回归模型族

与协同过滤仅利用用户和物品之间的显式或隐式反馈信息相比，逻辑回归能够利用和融合更多用户、物品及上下文特征。从LR 模型衍生出的模型同样“枝繁叶茂”，包括增强了非线性能力的大规模分片线性模型( Large Scale Piece-wise Linear Model, LS-PLM ），由逻辑回归发展出来的FM 模型，以及与多种不同模型配合使用后的组合模型，等等。

(3) 因子分解机模型族

因子分解机在传统逻辑回归的基础上，加入了二阶部分，使模型具备了进行特征组合的能力。更进一步，在因子分解机基础上发展出来的域感知因子分解机（ Field-aware Factorization Machi时， FFM ）则通过加入特征域的概念，进一步加强了因子分解机特征交叉的能力。

(4) 组合模型。

为了融合多个模型的优点，将不同模型组合使用是构建推荐模型常用的方法。Facebook 提出的GBDT+LR【梯度提升决策树（ Gradient Boosting Decision Tree）＋逻辑回归】组合模型是在业界影响力较大的组合方式。此外，组合模型中体现出的特征工程模型化的思想，也成了深度学习推荐模型的引子和核心思想之一。

2 协同过滤——经典的推荐算法

经典的协同过滤算法从物品相似度和用户相似度角度出发，分为物品协同过滤(ltemCF)和用户协同过滤(UserCF) 。

协同过滤使用的数据为用户与物品之间的交互矩阵，或称共现矩阵。以电商网站场景为例，用户作为矩阵行坐标，商品作为列坐标，将用户对物品评分数据转换为矩阵中相应的元素值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IY0ChSEn-1653567457048)(https://raw.githubusercontent.com/SNIKCHS/MDImage/main/img/CF_process.png)]

2.1 UserCF

2.1.1 用户相似度

UserCF中用户相似度的计算是算法中最关键的一步。常用的相似度计算方法有如下几种。

(1) 余弦相似度。余弦相似度(Cosine Similarity)衡量了用户向量t和用户向量j之间的向量夹角大小。显然，夹角越小，证明余弦相似度越大，两个用户越相似。

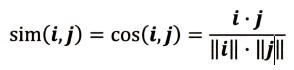
(2) 皮尔逊相关系数。相比余弦相似度，皮尔逊相关系数通过使用用户平均分对各独立评分进行修正，减小了用户评分偏置的影响。(有的用户总喜欢对所有物品打高分或者低分，通过消除偏置获取物品间相对的评分)

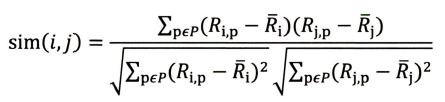
$R_{i,p}$代表用户i对物品p的评分。${\overline{R}}_i$代表用户i对所有物品的平均评分，P代表所有物品的集合。

(3) 基于皮尔逊系数的思路，还可以通过引入物品平均分的方式，减少物品评分偏置对结果的影响。

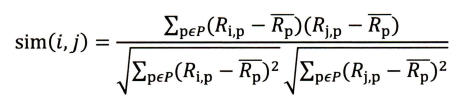
${\overline{R}}_p$代表物品p得到所有评分的平均分。

2.1.2最终结果的排序

在获得Top n 相似用户之后，假设“目标用户与其相似用户的喜好是相似的”，可根据相似用户的已有评价对目标用户的偏好进行预测。最常用的方式是利用用户相似度和相似用户的评价的加权平均获得目标用户的评价预测

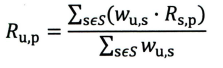
权重$w_{u,s}$是用户u和用户s的相似度，$R_{s,p}$是用户s对物品p的评分。在获得用户u对不同物品的评价预测后，最终的推荐列表根据预测得分进行排序即可得到。

2.1.3 UserCF的缺点

1. 互联网应用场景下一般用户数往往远大于物品数，而UserCF 需要维护用户相似度矩阵以便快速找出Top n 相似用户，存储开销非常大，为$n^2$
2. 用户的历史数据向量往往非常稀疏，对于只有几次购买或者点击行为的用户来说，找到相似用户的准确度是非常低的，这导致UserCF 不适用于那些正反馈获取较困难的应用场景

2.2 ItemCF

ItemCF 是基于物品相似度进行推荐的协同过滤算法。通过计算共现矩阵中物品列向量的相似度得到物品之间的相似矩阵，再找到用户的历史正反馈物品的相似物品进行进一步排序和推荐， ItemCF 的具体步骤如下：

( 1 ）基于历史数据，构建以用户（假设用户总数为m）为行坐标，物品（物品总数为n ） 为列坐标的m ×n 维的共现矩阵。

( 2 ）计算共现矩阵两两列向量间的相似性（相似度的计算方式与用户相似度的计算方式相同），构建n ×n 维的物品相似度矩阵。

( 3 ）获得用户历史行为数据中的正反馈物品列表。

( 4 ）利用物品相似度矩阵，针对目标用户历史行为中的正反馈物品，找出相似的Top k 个物品，组成相似物品集合。

( 5 ）对相似物品集合中的物品，利用相似度分值进行排序，生成最终的推荐列表。如果一个物品与多个用户行为历史中的正反馈物品相似，那么该物品最终的相似度应该是多个相似度的累加，如下式

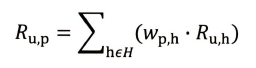
H 是目标用户的正反馈物品集合，$W_{p,h}$是物品p与物品h的物品相似度，$R_{u,h}$是用户u 对物品h 的已有评分。

2.3 UserCF与ItemCF的应用场景

UserCF 基于用户相似度进行推荐，使其具备更强的社交特性，用户能够快速得知与自己兴趣相似的人最近喜欢的是什么，即使某个兴趣点以前不在自己的兴趣范围内，也有可能通过“朋友”的动态快速更新自己的推荐列表。这样的特点使其非常适用于新闻推荐场景。因为新闻本身的兴趣点往往是分散的，相比用户对不同新闻的兴趣偏好，新闻的及时性、热点性往往是其更重要的属性，而UserCF 正适用于发现热点，以及跟踪热点的趋势。

另一方面， ItemCF 更适用于兴趣变化较为稳定的应用。比如在Amazon 的电商场景中，用户在一个时间段内更倾向于寻找一类商品，这时利用物品相似度为其推荐相关物品是契合用户动机的。在Netflix 的视频推荐场景中，用户观看电影、电视剧的兴趣点往往比较稳定，因此利用ItemCF 推荐风格、类型相似的视频是更合理的选择。

2.4 协同过滤的下一步发展

协同过滤是一个非常直观、可解释性很强的模型，但泛化能力较差，即无法将两个物品相似这一信息推广到其他物品的相似性计算上。这导致热门的物品具有很强的头部效应，容易跟大量物品产生相似性；而尾部的物品由于特征向量稀疏，很少与其他物品产生相似性，导致很少被推荐。协同过滤的天然缺陷一一推荐结果的头部效应较明显，处理稀疏向量的能力弱。

为解决上述问题，同时增加模型的泛化能力，矩阵分解技术被提出。该方法在协同过滤共现矩阵的基础上，使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在一定程度上弥补了协同过滤模型处理稀疏矩阵能力不足的问题。

另外，协同过滤仅利用用户和物品的交互信息，无法有效地引人用户年龄、性别、商品描述、商品分类、当前时间等一系列用户特征、物品特征和上下文特征，这无疑造成了有效信息的遗漏。为了在推荐模型中引入这些特征，推荐系统逐渐发展到以逻辑回归模型为核心的、能够综合不同类型特征的机器学习模型的道路上。

3 矩阵分解(MF)算法——协同过滤的进化

矩阵分解在协同过滤算法中“共现矩阵”的基础上，加入了隐向量的概念，加强了模型处理稀疏矩阵的能力，针对性地解决了协同过滤存在的主要问题。

3.1 矩阵分解算法原理

矩阵分解算法则期望为每一个用户和视频生成一个隐向量，将用户和视频定位到隐向量的表示空间上，距离相近的用户和视频表明兴趣特点接近，在推荐过程中把距离相近的视频推荐给目标用户。

隐向量是通过分解协同过滤生成的共现矩阵得到的

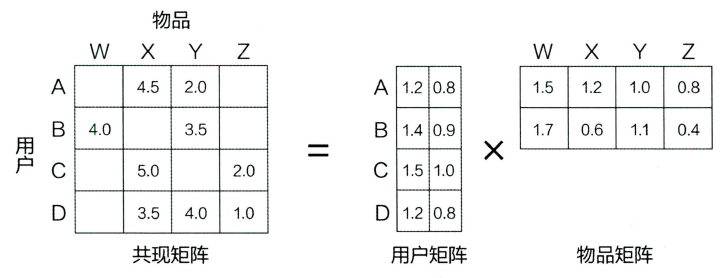
==矩阵分解算法将$m\times n$维的共现矩阵R 分解为$m\times k$维的用户矩阵U 和$k\times n$维的物品矩阵V 相乘的形式。==其中m是用户数量，n是物品数量， k 是隐向量的维度。k 的大小决定了隐向量表达能力的强弱。k 的取值越小，隐向量包含的信息越少，模型的泛化程度越高；反之， k 的取值越大，隐向量的表达能力越强，但泛化程度相应降低。此外， k 的取值还与矩阵分解的求解复杂度直接相关。

基于用户矩阵$\mathbf{U}\in {\mathbb{R}}^{n\times k}$和物品矩阵$\mathbf{V}\in {\mathbb{R}}^{m\times k}$，用户u 对物品i 的预估评分如下：

${\hat{r}}_{ui}=p_u{q}_i^T$

$p_u$是用户u 在用户矩阵U 中的对应行向量， $q_i$是物品i 在物品矩阵V中的对应行向量。

3.2 矩阵分解的求解过程

对矩阵进行矩阵分解的主要方法有三种：特征值分解（ Eigen Decomposition） 、奇异值分解（ Singular Value Decomposition , SYD ）和梯度下降（ Gradient Descent ） 。其中，特征值分解只能作用于方阵，显然不适用于分解用户－物品矩阵。

奇异值分解存在两点缺陷：

1. 奇异值分解要求原始的共现矩阵是稠密的。互联网场景下大部分用户的行为历史非常少，用户－物品的共现矩阵非常稀疏，这与奇异值分解的应用条件相悖。如果应用奇异值分解，就必须对缺失的元素值进行填充。
2. 传统奇异值分解的计算复杂度达到了$O(m{n}^2)$的级别，这对于商品数量动辄上百万、用户数量往往上千万的互联网场景来说几乎是不可接受的。

因此，梯度下降法成了进行矩阵分解的主要方法。

3.3 消除用户相物品打分的偏芜

为了消除用户和物品打分的偏差（ Bias ），常用的做法是在矩阵分解时加入用户和物品的偏差向量

${\hat{r}}_{ui}=\mu +b_i+bu+p_u{q}_i^T$

其中$\mu$是全局偏差常数，$b_i$是物品偏差系数，可使用物品i收到的所有评分的
均值， $b_u$是用户偏差系数，可使用用户u给出的所有评分的均值。

3.4矩阵分解的优点和局限性

相比协同过滤，矩阵分解有如下优点。

( 1 ）泛化能力强。在一定程度上解决了数据稀疏问题。

( 2 ）空间复杂度低。只需存储用户和物品隐向量。空间复杂度由$n^2$级别降低到$(n+m)\cdot k$级别。

( 3 ）更好的扩展性和灵活性。矩阵分解的最终产出是用户和物品隐向量，与深度学习中的Embedding 思想不谋而合，因此矩阵分解的结果也非常便于
与其他特征进行组合和拼接，并便于与深度学习网络进行无缝结合。

与此同时，也要意识到矩阵分解的局限性。与协同过滤一样，矩阵分解同样不方便加入用户、物品和上下文相关的特征，这使得矩阵分解丧失了利用很多有效信息的机会，同时在缺乏用户历史行为时，无法进行有效的推荐。为了解决这个问题，逻辑回归模型及其后续发展出的因子分解机等模型，凭借其天然的融合不同特征的能力，逐渐在推荐系统领域得到更广泛的应用。

4 逻辑回归——融合多种特征的推荐模塑

逻辑回归模型能够综合利用用户、物品、上下文等多种不同的特征，生成较为“全面”的推荐结果。

相比协同过滤和矩阵分解利用用户和物品的“相似度”进行推荐，逻辑回归将推荐问题看成一个分类问题，通过预测正样本的概率对物品进行排序。逻辑回归模型将推荐问题转换成了一个点击率（ Click Through Rate, CTR ）预估问题。

4.1基于逻辑回归模型的推荐流程

1. 将用户年龄、性别、物品属性、物品描述、当前时间、当前地点等特征
   转换成数值型特征向量。
2. 确定逻辑回归模型的优化目标（以优化“点击率”为例），利用已有样本数据对逻辑回归模型进行训练，确定逻辑回归模型的内部参数。
3. 在模型服务阶段，将特征向量输入逻辑回归模型，经过逻辑回归模型的推断，得到用户“点击”物品的概率。
4. 利用“点击”概率对所有候选物品进行排序，得到推荐列表。

4.2 逻辑回归模型的局限性

逻辑回归模型的表达能力不强，无法进行特征交叉、特征筛选等一系列较为“高级”的操作，因此不可避免地造成信息的损失。在进入深度学习时代之后，多层神经网络强大的表达能力可以完全替代逻辑回归模型

5 从FM 到FFM——自动特征交叉的解决方案

在仅利用单一特征而非交叉特征进行判断的情况下，有时不仅是信息损失的问题，甚至会得出错误的结论。

以辛普森悖论为例，在对样本集合进行分组研究时，在分组比较中都占优势的一方，在总评中有时反而是失势的一方。

无论男性用户还是女性用户，对视频B的点击率都高于视频A ， 显然推荐系统应该优先考虑向用户推荐视频B 。

但如果忽略性别这个维度，将数据汇总会发现视频A的点击率比视频B高

在辛普森悖论的例子中，分组实验相当于使用“性别” ＋ “视频id”的组合特征计算点击率， 而汇总实验则使用“视频id”这一单一特征计算点击率。汇总实验对高维特征进行了合井，损失了大量的有效信息，因此无法正确刻画数据模式。

逻辑回归只对单一特征做简单加权， 不具备进行特征交叉生成高维组合特征的能力， 因此表达能力很弱， 甚至可能得出像“辛普森悖论”那样的错误结论。因此需要通过改造逻辑回归模型，使其具备特征交叉的能力。

5.1 POLY2 模型一一特征交叉的开始

POLY2 模型的数学形式如下：

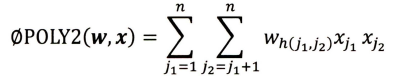
该模型对所有特征进行了两两交叉（特征$x_{j_1}$ 和$x_{j_2}$ ） ，并对所有的特征组合赋予权重$w_{h(j_1,j_2)}$ 。POLY2 通过暴力组合特征的方式，在一定程度上解决了特征组合的问题。POLY2 模型本质上仍是线性模型，其训练方法与逻辑回归并无区别，因此便于工程上的兼容。

但POLY2 模型存在两个较大的缺陷。

1. 在处理互联网数据时，经常采用one-hot 编码的方法处理类别型数据，致使特征向量极度稀疏， POLY2 进行元选择的特征交叉原本就非常稀疏的特征向量更加稀疏，导致大部分交叉特征的权重缺乏有效的数据进行训练，无法收敛。
2. 权重参数的数量由n 直接上升到肘，极大地增加了训练复杂度。

5.2 FM 模型——隐向量特征交叉

为了解决POLY2 模型的缺陷， 2010 年Rendle 提出了FM 模型。

下式是FM 二阶部分的数学形式，与POLY2 相比主要区别是用两个向量的内积（$w_{j_1}\cdot w_{j_2}$）取代了单一的权重系数$w_{h(j_1,j_2)}$ 。FM 为每个特征学习了一个隐权重向量（ latent vector ）。在特征交叉时，使用两个特征隐向量的内积作为交叉特征的权重。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6Ceuoxk3-1653567457050)(https://raw.githubusercontent.com/SNIKCHS/MDImage/main/img/FM.png)]

本质上， FM引入隐向量的做法，与矩阵分解用隐向量代表用户和物品的做法异曲同工。可以说， FM 是将矩阵分解隐向量的思想进行了进一步扩展，从单
纯的用户、物品隐向量扩展到了所有特征上。

FM 通过引入特征隐向量的方式，把POLY2 模型$n^2$级别的权重参数数量减少到了nk ( k 为隐向量维度， n>>k ）。在使用梯度下降法进行FM 训练的过程中， FM 的训练复杂度同样可被降低到nk级别，极大地降低了训练开销。

隐向量的引入使FM能更好地解决数据稀疏性的问题。在POLY2 中，只有当两种特征同时出现在一个训练样本中时模型才能学到这个组合特征对应的权重；而在FM 中，隐向量可以单独更新，这大幅降低了模型对数据稀疏性的要求。甚至具备计算从未出现过的特征组合权重的能力。相比POLY2, FM 虽然丢失了某些具体特征组合的精确记忆能力，但是泛化能力大大提高。

5.3 FFM模型——引入特征域的概念

相比FM 模型， FFM 模型引入了特征域感知（ field-aware ）这一概念，使模型的表达能力更强。

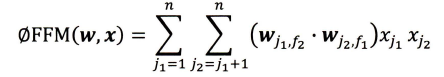
FFM与FM 的区别在于隐向量由原来的$w_{j_1}$变成了$w_{j_1,f_2}$这意味着每个特征对应的不是唯一一个隐向量，而是一组隐向量。当$x_{j_1}$特征与$x_{j_2}$特征进行交叉时，$x_{j_1}$特征会从$x_{j_1}$ 的这一组隐向量中挑出与特征$x_{j_2}$的域$f_2$对应的隐向量$w_{j_1,f_2}$进行交叉。同理， $x_{j_2}$也会用与$x_{j_1}$的域$f_2$对应的隐向量进行交叉。特征域也就是特征的种类。

在FFM 模型的训练过程中，需要学习n个特征在f个域上的k维隐向量，参数数量共$n\cdot k\cdot f$个。在训练方面， FFM 的二次项并不能像FM 那样简化，因此其复杂度为$k{n}^2$。

相比FM, FFM 引入了特征域的概念，为模型引入了更多有价值的信息，使模型的表达能力更强，但与此同时，FFM 的计算复杂度上升到$k{n}^2$，远大于FM的kn 。在实际工程应用中，需要在模型效果和工程投入之间进行权衡。

6 GBDT+LR——特征工程模型化的开端

FFM 模型采用引入特征域的方式增强了模型的特征交叉能力，但无论如何，FFM 只能做二阶的特征交叉，如果继续提高特征交叉的维度，会不可避免地产生组合爆炸和计算复杂度过高的问题。为了做到有效处理高维特征组合和筛选的问题呢，2014 年，Facebook 提出了基于GBDT+ LR组合模型的解决方案。

6.1 GBDT+LR 组合模型的结构

该模型利用GBDT 自动进行特征筛选和组合，进而生成新的离散特征向量，再把该特征向量当作LR 模型输入，预估CTR

用GBDT 构建特征工程，利用LR 预估CTR 这两步是独立训练的，所以不存在如何将LR 的梯度回传到GBDT 这类复杂的问题。

GBDT 的基本结构是决策树组成的树林， 学习的方式是梯度提升。(损失函数为二分之一平方误差，步长为1时，梯度下降法跟梯度提升是等价的。梯度提升的目的也是梯度下降，只不过相比于普通梯度下降通过直接更新参数来梯度下降，梯度提升通过累加弱学习器来梯度下降。)

GBDT是由多棵回归树组成的树林，后一棵树以前面树林的结果与真实结果的残差为拟合目标。每棵树生成的过程是一棵标准的回归树生成过程，因此回归树中每个节点的分裂是一个自然的特征选择的过程，而多层节点的结构则对特征进行了有效的自动组合。GBDT预测的方式是把所有子树的结果加起来，

6.2 GBDT 迸行特征转换的过程

GBDT 模型可以完成从原始特征向量到新的离散型特征向量的转化。

即用一个离散特征表示一串组合特征：

• 苹果重量509g，颜色红—>【500g<=苹果重量<750g，红色】==[0,1,0,0]
• 苹果重量450g，颜色绿—>【苹果重量<500g，绿色】== [0,0,0,1]

一个训练样本在输入GBDT 的某一子树后，会根据每个节点的规则最终落入某一叶子节点，把该叶子节点置为1，其他叶子节点置为0 ，所有叶子节点组成的向量即形成了该棵树的特征向量， 把GBDT 所有子树的特征向量连接起来，即形成了后续LR 模型输入的离散型特征向量。

以下图为例， GBDT 由三棵子树构成每棵子树有4 个叶子节点，输入一个训练样本后，其先后落入“子树1 ”的第3 个叶节点中，那么特征向量就是[0,0,1,0]，“子树2”的第1个叶节点，特征向量为[1,0,0,0]，“子树3 ”的第4 个叶节点，特征向量为[0,0,0,1]，最后连接所有特征向量，形成最终的特征向量[0,0,1,0,1,0,0,0,0,0,0,1]。

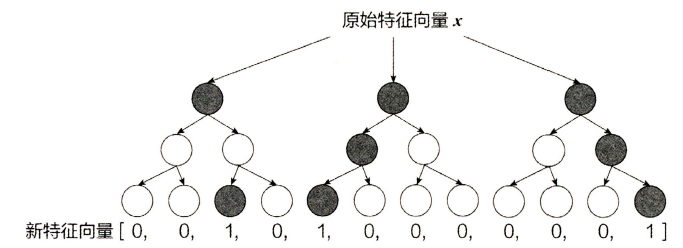
决策树的深度决定了特征交叉的阶数。如果决策树的深度为4 ，则通过3 次节点分裂，最终的叶节点实际上是进行三阶特征组合后的结果。GBDT拥有比FM强的特征组合能力，但GBDT 容易产生过拟合，以及GBDT 的特征转换方式实际上丢失了大量特征的数值信息。

6.3 GBDT+LR 组合模型开启特征工程新趋势

GBDT+LR 组合模型对于推荐系统领域的重要性在于，它大大推进了特征工程模型化这一重要趋势。在GBDT+LR 组合模型出现之前，特征工程的主要解决方法有两个： 一是进行人工的或半人工的特征组合和特征筛选； 二是通过改造目标函数，改进模型结构，增加特征交叉项的方式增强特征组合能力。但这两种方法都有弊端，第一种方法对算法工程师的经验和精力投入要求较高；第二种方法则要求从根本上改变模型结构，对模型设计能力的要求较高。

GBDT+LR 组合模型的提出，意味着特征工程可以完全交由一个独立的模型来完成，模型的输入可以是原始的特征向量，不必在特征工程上投入过多的人工筛选和模型设计的精力，实现真正的端到端（ End to End ）训练。

7 LS-PLM——阿里巴巴曾经的主流推荐模型

LS-PLM曾是阿里巴巴的主流推荐模型，其结构与三层神经网络极其相似，可以将它看作推荐系统领域连接深度学习时代的节点。

7.1 LS-PLM模型的主要结构

LS-PLM 又被称为MLR ( Mixed Logistic Regression ，混合逻辑回归）模型。本质上， LS-PLM 可以看作对逻辑回归的自然推广，它在逻辑回归的基础上采用分而治之的思路，先对样本进行分片，再在样本分片中应用逻辑回归进行CTR预估。

在逻辑回归的基础上加入聚类的思想，其灵感来自对广告推荐领域样本特点的观察。举例来说，如果CTR 模型要预估的是女性受众点击女装广告的CTR;那么显然，我们不希望把男性用户点击数码类产品的样本数据也考虑进来，因为这样的样本不仅与女性购买女装的广告场景毫无相关性，甚至会在模型训练过程中扰乱相关特征的权重。==为了让CTR 模型对不同用户群体、不同使用场景更有针对性，其采用的方法是先对全量样本进行聚类，再对每个分类施以逻辑回归模型进行CTR 预估。==LS-PLM 的实现思路就是由该灵感产生的。

LS-PLM 的数学形式如下图所示，首先用聚类函数π 对样本进行分类（这里的π 采用了softmax 函数对样本进行多分类），再用LR 模型计算样本在分片中具体的CTR ，然后将二者相乘后求和。

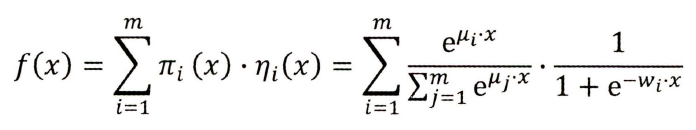
其中的超参数“分片数” m 可以较好地平衡模型的拟合与推广能力。当m=1时， LS-PLM 就退化为普通的逻辑回归。m 越大，模型的拟合能力越强。与此同时，模型参数规模也随m的增大而线性增长，模型收敛所需的训练样本也随之增长。在实践中，阿里巴巴给出的m 的经验值为12 。

7.2 LS-PLM模型的优点

LS-PLM 模型适用于工业级的推荐、广告等大规模稀疏数据的场景，主要是因为其具有以下两个优势。

1. 端到端的非线性学习能力： LS-PLM 具有样本分片的能力，因此能够挖掘出数据中蕴藏的非线性模式，省去了大量的人工样本处理和特征工程的过程，使LS-PLM 算法可以端到端地完成训练，便于用一个全局模型对不同应用领域、业务场景进行统一建模。
   就退化为普通的逻辑回归。m 越大，模型的拟合能力越强。与此同时，模型参数规模也随m的增大而线性增长，模型收敛所需的训练样本也随之增长。在实践中，阿里巴巴给出的m 的经验值为12 。

7.2 LS-PLM模型的优点

LS-PLM 模型适用于工业级的推荐、广告等大规模稀疏数据的场景，主要是因为其具有以下两个优势。

1. 端到端的非线性学习能力： LS-PLM 具有样本分片的能力，因此能够挖掘出数据中蕴藏的非线性模式，省去了大量的人工样本处理和特征工程的过程，使LS-PLM 算法可以端到端地完成训练，便于用一个全局模型对不同应用领域、业务场景进行统一建模。
2. 模型的稀疏性强： LS-PLM 在建模时引入了L1 和L2,1 范数，可以使最终训练出来的模型具有较高的稀疏度，使模型的部署更加轻量级。模型服务过程仅需使用权重非零特征，因此稀疏模型也使其在线推断的效率更高。