数据处理
对于一组数据,只有时间戳和加速度,怎么样进行傅立叶变换分析? 参考信号处理内容,首先模拟一组数据进行分析。
以下数据两个频率为1Hz与100Hz,经过采样和傅立叶变化之后,捕捉到信号对应的频率为1Hz与100Hz(还有其他信号)。
close all;
t = 0:0.01:3; % 真实世界时间
f1 = 1; % 频率
f2 = 200;
f3 = 50; % 设定两个复信号
f4 = -60;
F = @(t)(sin(2*pi*f1*t) + sin(2*pi*f2*t)+ exp(j*2*pi*f3*t) + exp(j*2*pi*f4*t)); % 信号函数
y = F(t); % 生成信号
% figure;subplot(3,1,1);plot(t , y); % 信号真实图
fs = 1000; % 采样率
dtc = 1/fs; % 采样间隔时间
tc = 0:dtc:4; % 采样时间序列
yc = F(tc); % 采样信号序列
%% 傅立叶变换以及画图
figure;
N = length(yc);
x = (-N/2+1:N/2)/N*fs;
semilogy(x , abs(fftshift(fft(yc))));
我们可以看到,复信号在幅度谱上表现是只有单侧有信号。而实信号在幅度谱上两侧均有信号。
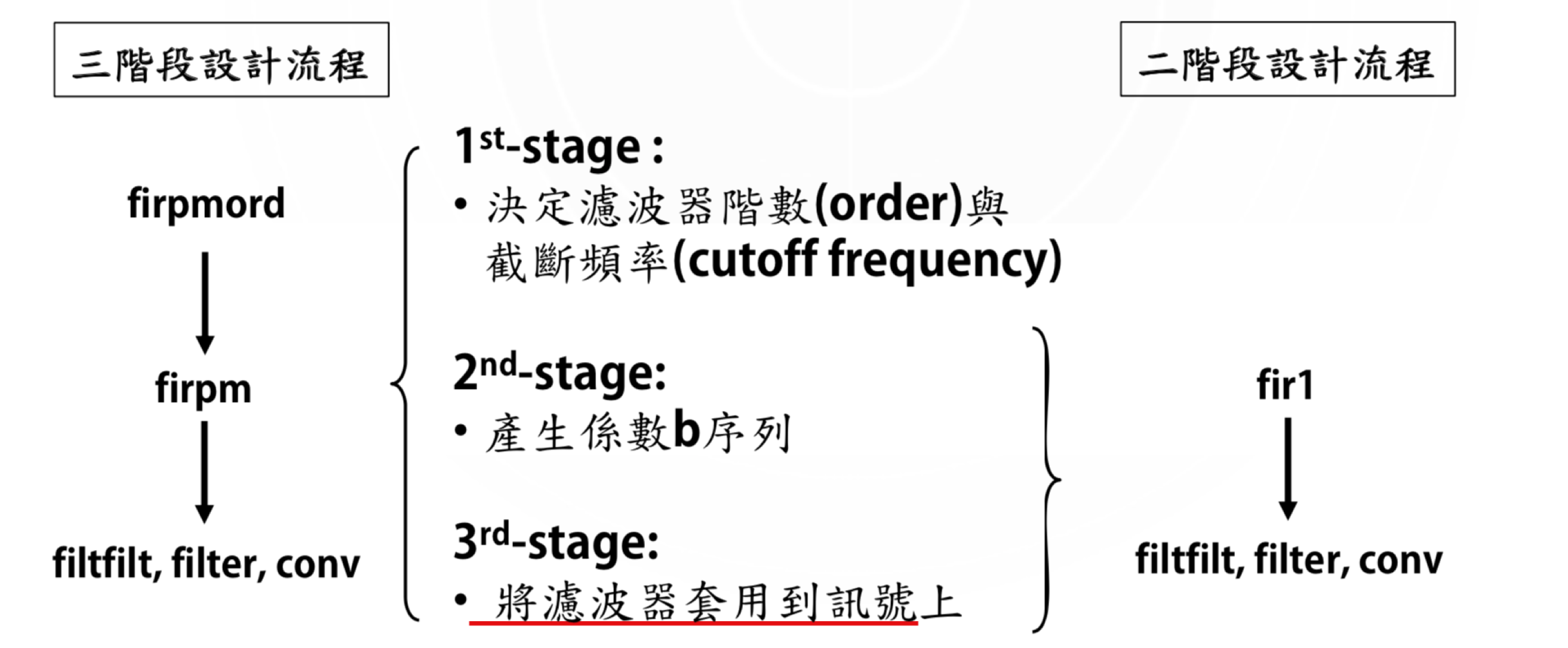
那么如何对数据进行信号处理呢?如何用fdatool设计滤波器?
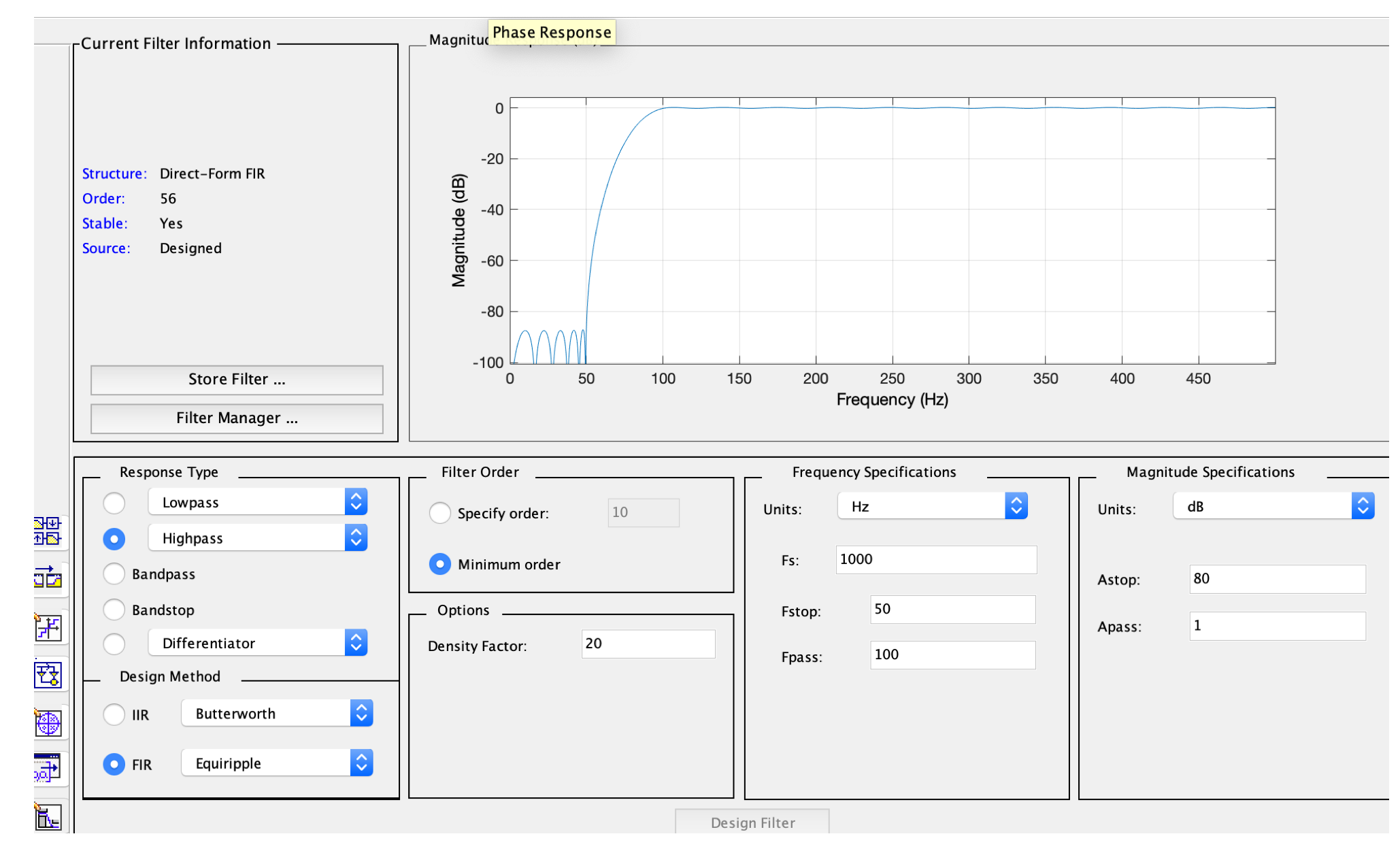
频域上表现如下:
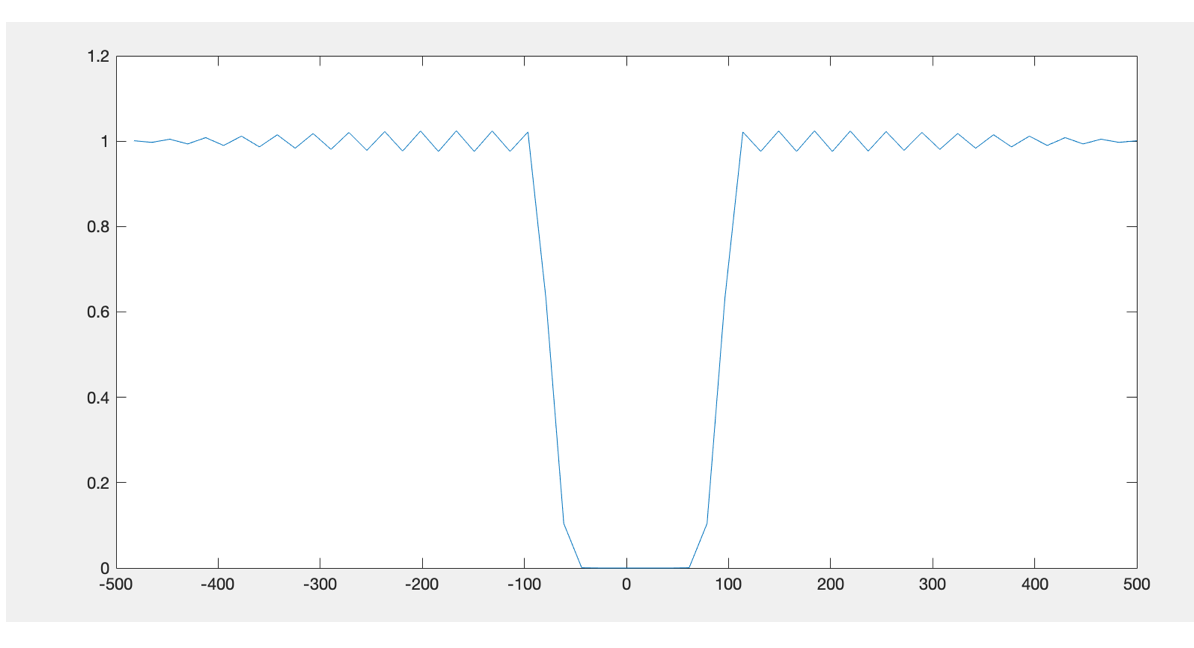
设计上述高通滤波器,与所有数据进行卷积,完成滤波。得到结果如下:
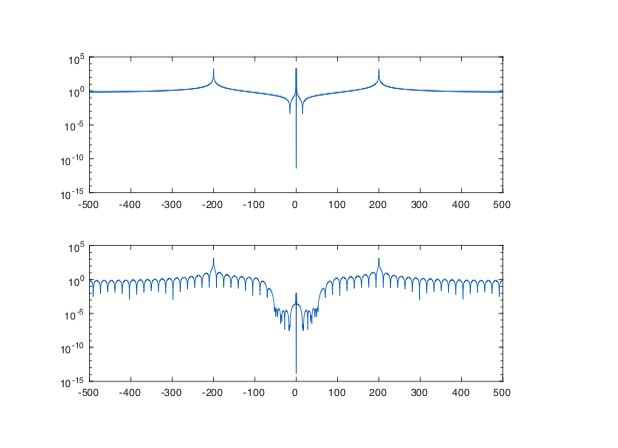
Fs = 1000; % Sampling Frequency
Fstop = 50; % Stopband Frequency
Fpass = 100; % Passband Frequency
Dstop = 0.0001; % Stopband Attenuation
Dpass = 0.057501127785; % Passband Ripple
dens = 20; % Density Factor
% Calculate the order from the parameters using FIRPMORD.
[N, Fo, Ao, W] = firpmord([Fstop, Fpass]/(Fs/2), [0 1], [Dstop, Dpass]);
% Calculate the coefficients using the FIRPM function.
b = firpm(N, Fo, Ao, W, {dens});
Hd = dfilt.dffir(b);
yf = conv( b , yc);% 滤波后的信号
信号时域频域的关系如下:
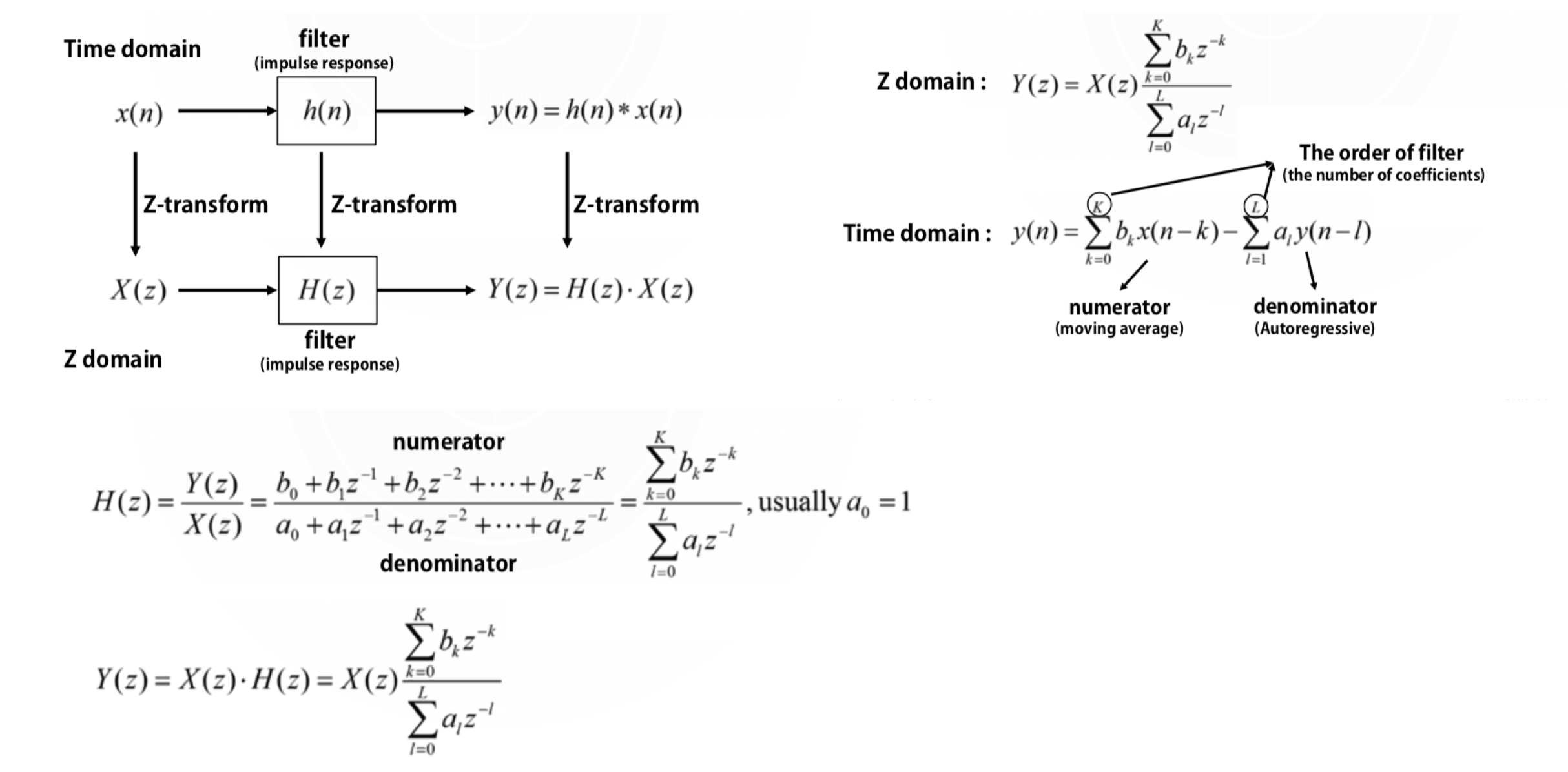
因此经常设计的滤波器一般有如下形式:
H(z)=0.2+0.5z−11−0.2z−1+0.8z−2H(z)=\frac{0.2+0.5 z^{-1}}{1-0.2 z^{-1}+0.8 z^{-2}}H(z)=1−0.2z−1+0.8z−20.2+0.5z−1
对应代码为:
clear, close all
%% initialize parameters
% 载波频率
samplerate = 1000; % in Hz 采样率
N = 512; % number of points, must be even, better be power of 2
%% define a and b coeffients of H (transfer function)
a = [1 -0.2 0.8]; % denominator terms
b = [0.2 0.5]; % numerator terms
%% option 1:compute the spectrum of H using fft
% H = fft(b,N)./fft(a,N); % compute H(f)
%
% mag = 20*log10(abs(H)); % get magnitude of spectrum in dB
% % 因为相位的变化会带来一定的相位偏移
% phase = angle(H)*2*pi; % get phase in deg.
%
% faxis = samplerate/2*linspace(0,1,N/2); % the axis of frequency
%% 或者下面:
N = 512;
[h1 , ftp] = freqz(b,1,N,fs);
mag = 20*log10(abs(h1)); % get magnitude of spectrum in dB
phase = angle(h1)/pi*180; % get phase in deg.
figure,
subplot(2,1,1),plot(ftp,mag)
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
grid on
subplot(2,1,2),plot(ftp,phase,'r')
xlabel('Frequency (Hz)'),ylabel('Phase (deg.)')
grid on
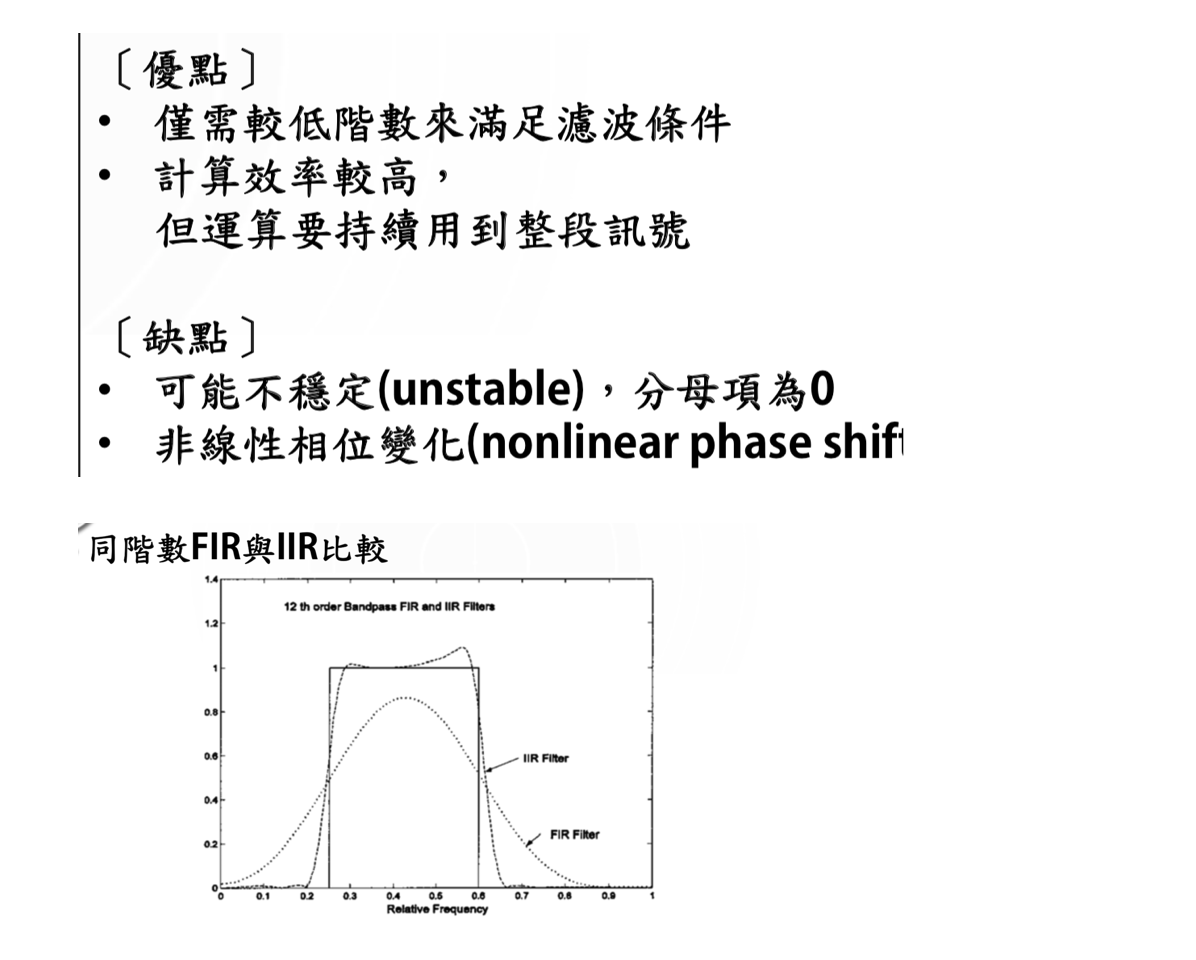
FIR滤波器
特点如下:

转换函数为:
H(z)=∑k=0Kbkz−kH(z)=\sum_{k=0}^{K} b_{k} z^{-k}H(z)=∑k=0Kbkz−k
对于上述fdatool设计的FIR滤波器,a为0,所以只用b进行卷积运算。下面画出了相位谱和幅度谱,下面作为示例。
%% 设计滤波器(FIR)
N = 512;
a = 1;
H = fft(b,N)/fft(a,N); % H矩阵
mag = 20*log10(abs(H)); % get magnitude of spectrum in dB 幅值
phase = angle(H)*2*pi; % get phase in deg.相位
faxis = samplerate/2*linspace(0,1,N/2); % the axis of frequency
%% plot the spectrum of H
figure,
subplot(2,1,1),plot(faxis,mag(1:N/2))
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
grid on
subplot(2,1,2),plot(faxis,phase(1:N/2),'r')
xlabel('Frequency (Hz)'),ylabel('Phase (deg.)')
grid on
滤波器设计离不开这个函数,具有特殊性质的函数sinc(t),如下:

所以设计以下低通滤波器:
b(k)=sin[2πfcTs(k−L/2)]π(k−L/2)b(k)=\frac{\sin \left[2 \pi f_{c} T_{s}(k-L / 2)\right]}{\pi(k-L / 2)}b(k)=π(k−L/2)sin[2πfcTs(k−L/2)]
fc代表截断频率,代码如下:
L = 57;
fs = 1000;
f2 = 100;
for k = 1:L
b(k) = sin(2*pi*f2*dtc*(k - L/2))/(pi*(k-L/2));
end
figure;
N = length(b);
x = (-N/2+1:N/2)/N*fs;
semilogy( x,abs(fftshift(fft(b))))
% 加窗
faxis = fs/2*linspace(0,1,N/2);
HW = fft(b.*hamming( length(b) )',N);
mag = 20*log10(abs(HW));
figure
plot(faxis,mag(1:N/2))
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
grid on
设计过程,可以参考下面:
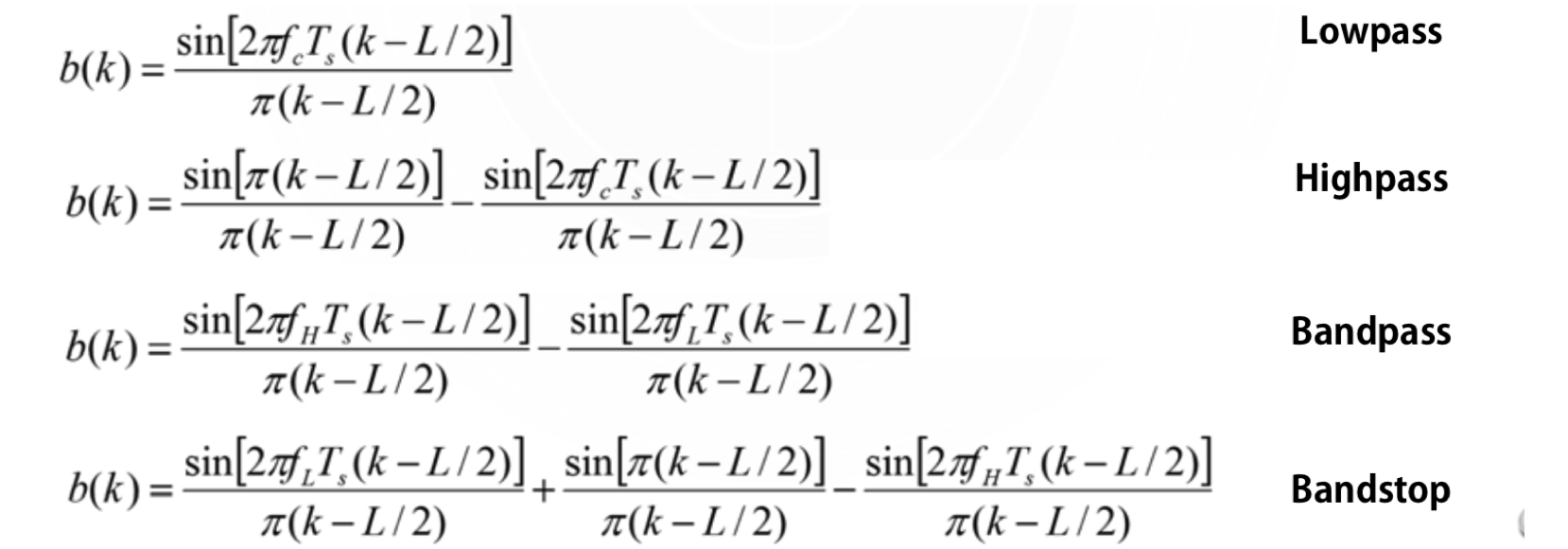
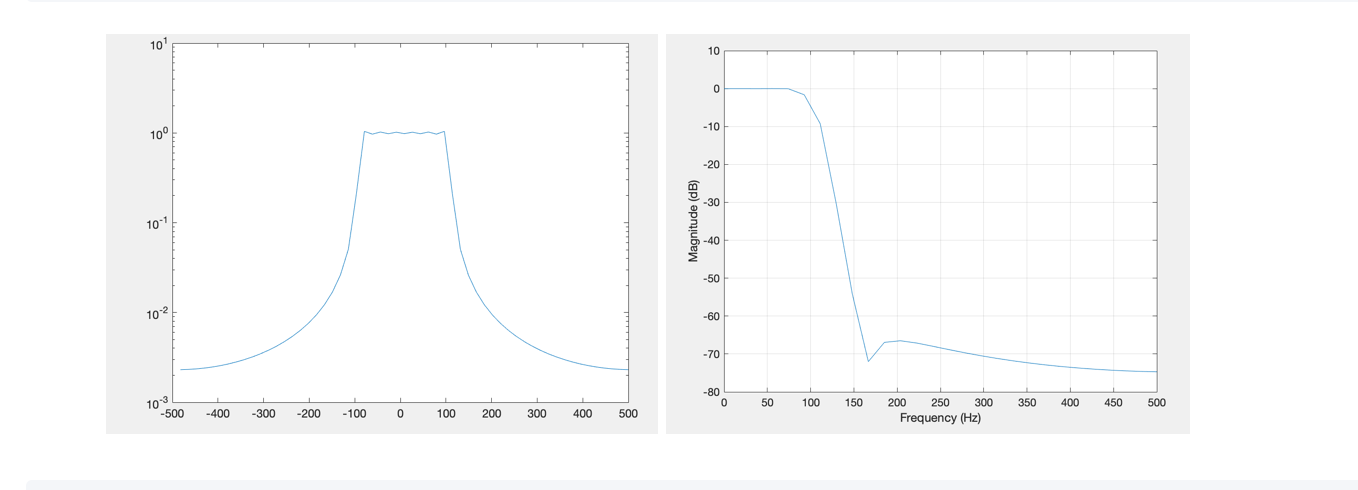
那么如何利用matlab代码生成滤波器?
fl=75; % low-cutoff frequency
fh=165; % high-cutoff frequency
trans_width=20; % in Hz. It is a half of transition band. if data length is not long enough, increase trans_width
rp=1; % in dB
rs=40; % in dB
%%% lowpass filter
[data_3sFIR,forder] = filter_3sFIR(data,[fl-trans_width fl+trans_width],[1 0],[0.1 0.001],samplerate);
%%% bandpass filter
[data_3sFIR,forder] = filter_3sFIR(data,[fl-trans_width fl+trans_width fh-trans_width fh+trans_width],[0 1 0],[0.001 0.1 0.001],samplerate);
%%% highpass filter
[data_3sFIR,forder] = filter_3sFIR(data,[fh-trans_width fh+trans_width],[0 1],[0.001 0.1],samplerate);
%%% bandstop filter
[data_3sFIR,forder] = filter_3sFIR(data,[fl-trans_width fl+trans_width fh-trans_width fh+trans_width],[1 0 1],[0.1 0.001 0.1],samplerate);
IIR 无限滤波器
%%% lowpass filter
[data_3sIIR,forder] = filter_3sIIR(data,fl-trans_width,fl+trans_width,rp,rs,samplerate,'low');
%%% bandpass filter
[data_3sIIR,forder] = filter_3sIIR(data,[fl+trans_width fh-trans_width],[fl-trans_width fh+trans_width],rp,rs,samplerate,'bandpass');
%%% highpass filter
[data_3sIIR,forder] = filter_3sIIR(data,fh+trans_width,fh-trans_width,rp,rs,samplerate,'high');
%%% bandstop filter
[data_3sIIR,forder] = filter_3sIIR(data,[fl-trans_width fh+trans_width],[fl+trans_width fh-trans_width],rp,rs,samplerate,'stop');
%% 简单如下
%% filter
sigfilter1=filter_2sIIR(EEGdata',fh,samplerate,forder,'low')';
sigfilter2=filter_2sIIR(EEGdata',fl,samplerate,forder,'high')';
sigfilter3=filter_2sIIR(EEGdata',[fl fh],samplerate,forder,'bandpass')';
小波变换
当信号随着时间发生变化时,可能信号的频率随着时间在不断增大,如何观测信号中的频率?其中低频的层粉需要较长的时间测量。
大概得到如下的结果:
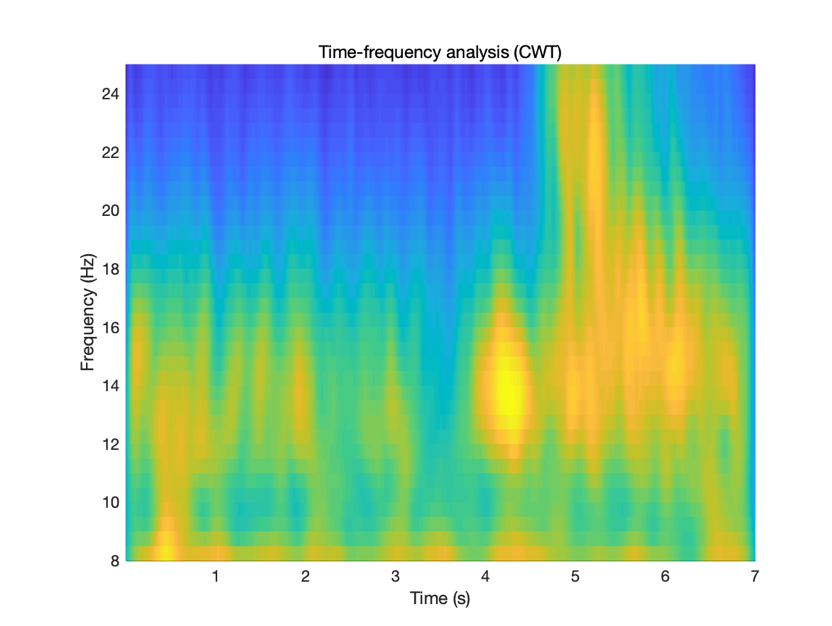
滤波器设计
容易想到的是,在这里做的数据的卷积处理,放在c语言中肯定是不合理的。那么在轨检模型中是如何完成计算的?怎么样与之同步起来?
下面给出了两个滤波器设计:
% FMIctrl中的滤波器幅频频特性
% ---------- 10 Hz(对于什么?) -------
fs = 500;
N = 80000;
b10 = [40000 0 0];
a10 = [4010000 -7600000 3610000];
[h10 f10]= freqz(b10,a10,N,'whole',fs);
%
mag = 20*log10(abs(h10)); % get magnitude of spectrum in dB
phase = angle(h10)/pi*180; % get phase in deg.
figure,
subplot(2,1,1),semilogx(f10,mag)
xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
grid on
subplot(2,1,2),semilogx(f10,phase,'r')
xlabel('Frequency (Hz)'),ylabel('Phase (deg.)')
grid on
suptitle('10Hz');
% ----------20 Hz-----------
coef1 = 40000;coef2= 1800000;
coef3=810000 ;coef4=10340000 ;
b20 = [coef1 0 0];
a20 = [coef4 -coef2 coef3];
figure();
[h20 f20]= freqz(b20,a20,N,'whole',fs);
subplot(2,1,1);semilogx(f20,20*log10(abs(h20)));xlabel('Frequency (Hz)'),ylabel('Magnitude (dB)')
subplot(2,1,2);semilogx(f20,angle(h20)*180/pi);xlabel('Frequency (Hz)'),ylabel('Phase (deg.)')
suptitle('20Hz');grid on;
模拟滤波器与数字滤波
模拟滤波器如下所示:
H(s)=B(s)A(s)=b(1)sn+b(2)sn−1+⋯+b(n+1)a(1)sm+a(2)sm−1+⋯+a(m+1)H(s)=\frac{B(s)}{A(s)}=\frac{b(1) s^{n}+b(2) s^{n-1}+\dots+b(n+1)}{a(1) s^{m}+a(2) s^{m-1}+\dots+a(m+1)}H(s)=A(s)B(s)=a(1)sm+a(2)sm−1+⋯+a(m+1)b(1)sn+b(2)sn−1+⋯+b(n+1)
由于存在:
λ=vttbs\lambda=v t_{t b s}λ=vttbs
二阶低通滤波器代码如下,该滤波器是从模拟滤波器转换而来。
% 二阶低通滤波器
w2 = (10^5)/(2^14);
v1= 15/3.6;
t1= 0.25/v1;
w2t1 = w2*t1;
b2 = [(w2t1)^2 0 0];
a2 = [1+w2t1+(w2t1)^2 ,- (2 + w2t1) ,1];
[h2 f2] = freqz(b2,a2,800000,500);
figure;suptitle ('二阶数字抗混叠滤波器和补偿滤波器');
semilogx(v1./f2,20*log10(abs(h2)));hold on;
标签:滤波器,filter,width,matlab,fh,trans,data,fdatool
来源: https://blog.csdn.net/chenshiming1995/article/details/104802212