数据挖掘：特征工程——特征处理与特征构建

这里贴一张网上特征工程的流程，供大家学习。

一、什么是特征工程

特征工程：其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。。就是获取更好的训练数据。主要有两个方面：

1. 获取更好的数据
2. 使机器学习算法达到最优

二、特征工程处理的意义

有这么一句话在业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。

1. 特征越好，灵活性越强
   只要特征选得好，即使是一般的模型（或算法）也能获得很好的性能，因为大多数模型（或算法）在好的数据特征下表现的性能都还不错。好特征的灵活性在于它允许你选择不复杂的模型，同时运行速度也更快，也更容易理解和维护。
2. 特征越好，构建的模型越简单
   有了好的特征，即便你的参数不是最优的，你的模型性能也依然会表现的很nice，所以你就不需要花太多的时间去寻找最有参数，这大大的降低了模型的复杂度，使模型趋于简单。
3. 特征越好，模型的性能越出色
   显然，这一点是毫无争议的，我们进行特征工程的最终目的就是提升模型的性能。

三、特征工程处理流程

特征工程处理流程主要包括以下四个方面特征处理，特征生成，特征提取，特征选择。本文主要介绍前两种方法。

四、特征处理与特征构建

在探索性数据分析中，我们已经对数据有了很深的了解，接下来要对数据中的特征进行处理和生成。

特征处理主要对数字，类别，顺序，时间序列，文本等类型数据进行处理，使得数据更适合模型的预测。
特征构建/衍生/生成：是根据对数据的了解，人为定出一些有意义的特征。这部分在之前探索性数据分析中有提到，其实进行EDA的目的就是为了更好地了解数据。

注：特征处理中也包含了特征清洗这一步骤，跟之前的数据预处理是一样的。关于这些没有太过明确的定义，主要学习整个处理数据的流程即可，不用对概念中的处理方式太过纠结。

4.1 数字特征的处理和构建

4.1.1 数据标准化、归一化

在数据挖掘数据处理过程中，不同评价指标往往具有不同的量纲和量纲单位，这样的情况会影响到数据分析的结果，为了消除指标之间的量纲影响，需要进行数据标准化处理，以解决数据指标之间的可比性。

数据标准化处理主要包括数据同趋化处理和无量纲化处理两个方面。

1. 数据同趋化处理主要解决不同性质数据问题，对不同性质指标直接加总不能正确反映不同作用力的综合结果，须先考虑改变逆指标数据性质，使所有指标对测评方案的作用力同趋化，再加总才能得出正确结果。
2. 数据无量纲化处理主要解决数据的可比性。经过上述标准化处理，原始数据均转换为无量纲化指标测评值，即各指标值（各特征）都处于同一个数量级别上，可以进行综合对比分析。

常见的数据标准化处理（这里先统称为数据标准化处理，其实数据标准化，归一化，中心化不一样）有以下四种，可以取消由于量纲不同、自身变异或者数值相差较大所引起的误差。

1.实现中心化和正态分布的Z-score
2.实现归一化的Max-Min
3.用于稀疏矩阵的MaxAbs
4.针对离群点的RobustScaler

sklearn的preprocessing提供了可以满足需求的方法。先用训练集训练标准化的类，然后用训练好的类分别转化训练集和测试集.

中心化：把数据整体移动到以0为中心点的位置。将数据减去这个数据集的平均值。
标准化：把整体的数据的中心移动到0，数据再除以一个数。在数据中心化之后，数据再除以数据集的标准差。
归一化：把数据的最小值移动到0，再除以数据集的最大值。对这个数据集的每一个数减去min，然后除以极差。
中心化、标准化、归一化定义

4.1.1.1 中心化与标准化(归一化)的处理意义

1.提升模型收敛速度
如下图，x1的取值为0-2000，而x2的取值为1-5，假如只有这两个特征，对其进行优化时，会得到一个窄长的椭圆形，导致在梯度下降时，梯度的方向为垂直等高线的方向而走之字形路线，这样会使迭代很慢，相比之下，右图的迭代就会很快（理解：也就是步长走多走少方向总是对的，不会走偏）。

2.提升模型精度
这在涉及到一些距离计算的算法时效果显著，比如算法要计算欧氏距离，如SVM，KNN等。上图中x2的取值范围比较小，涉及到距离计算时其对结果的影响远比x1带来的小，所以这就会造成精度的损失。所以归一化很有必要，他可以让各个特征对结果做出的贡献相同。而基于树的模型，可以不进行标准化，例如随机森林，bagging 和 boosting等。以 C4.5 算法为例，决策树在分裂结点时候主要依据数据集 D 关于特征 x 的信息增益比，而信息增益比和特征是否经过归一化是无关的，归一化不会改变样本在特征 x 上的信息增益。

在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用。因此，为了保证结果的可靠性，需要对原始指标数据进行标准化处理。

从经验上说，归一化是让不同维度之间的特征在数值上有一定比较性，可以大大提高分类器的准确性。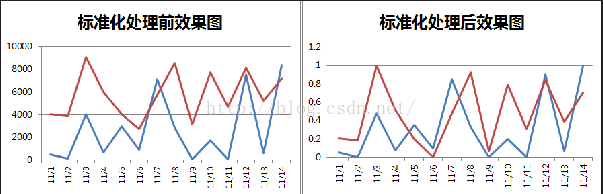

3. 深度学习中数据归一化可以防止模型梯度爆炸。

通过中心化和标准化处理，最终得到均值为0，标准差为1的服从标准正态分布的数据。可以取消由于量纲不同、自身变异或者数值相差较大所引起的误差。

在一些实际问题中，我们得到的样本数据都是多个维度的，即一个样本是用多个特征来表征的。比如在预测房价的问题中，影响房价的因素（特征）有房子面积、卧室数量等，很显然，这些特征的量纲和数值得量级都是不一样的，在预测房价时，如果直接使用原始的数据值，那么他们对房价的影响程度将是不一样的，而通过标准化处理，可以使得不同的特征具有相同的尺度（Scale）。简言之，当原始数据不同维度上的特征的尺度（单位）不一致时，需要标准化步骤对数据进行预处理。

下图中以二维数据为例：左图表示的是原始数据；中间的是中心化后的数据，数据被移动大原点周围；右图将中心化后的数据除以标准差，得到为标准化的数据，可以看出每个维度上的尺度是一致的（红色线段的长度表示尺度）。
其实，在不同的问题中，中心化和标准化有着不同的意义，比如在训练神经网络的过程中，通过将数据标准化，能够加速权重参数的收敛。对数据进行中心化预处理，这样做的目的是要增加基向量的正交性。

中心化 -PCA示例
下面两幅图是数据做中心化（centering）前后的对比，可以看到其实就是一个平移的过程，平移后所有数据的中心是（0，0）

在做PCA时，我们需要找出矩阵的特征向量，也就是主成分（PC）。比如说找到的第一个特征向量是a = [1, 2]，a在坐标平面上就是从原点出发到点 (1,2)的一个向量。
如果没有对数据做中心化，那算出来的第一主成分的方向可能就不是一个可以“描述”（或者说“概括”）数据的方向。
黑色线就是第一主成分的方向。只有中心化数据之后，计算得到的方向才能比较好的“概括”原来的数据。

中心化与标准化(归一化)的处理意义

4.1.1.2 Z-Score

Z-Score：即标准化。它是基于原始数据的均值和标准差，通过减去均值然后除以方差（或标准差），这种数据标准化方法经过处理后数据，符合标准正态分布，即均值为0，标准差为1。转化函数为：x =(x - ?)/?

注：

• 使用最多，处理后的数据均值为0，标准差为1.
• 其使用前提最好是特征值服从正态分布，只有原始数据是正态分布，转换后的数据才是标准正态，不然，即使进行转化，得到的也不是标准正态。
• 另外，如果数据中有较多异常值，此时直接做z-score标准化得到的高斯分布将偏离正常范围。改变了原始数据的结构，因此不适宜用于对稀疏矩阵做数据预处理。
  通常这种方法基本可用于有outlier的情况，但是，在计算方差和均值的时候outliers仍然会影响计算。所以，在出现outliers的情况下可能会出现转换后的数的不同feature分布完全不同的情况。
  如下图，经过StandardScaler之后，横坐标与纵坐标的分布出现了很大的差异，这可能是outliers造成的。
  

#Z-score标准化
zscore_scaler=preprocessing.StandardScaler()     #建立StandarScaler对象
data_scale_1=zscore_scaler.fit_transform(data)   #StandardScaler标准化处理

4.1.1.3 Max-Min

Max-Min：即区间缩放/归一化。该方法是用数据的最大值和最小值对原始数据进行预处理其是一种线性变换，将特征的取值区间缩放到某个特点的范围，例如[0, 1]等。转换函数为:x = (x-min)/(max-min)相当于将整体分布移动到从0开始的位置，但数据分布未变化，保留原始数据的结构。
注：

• 这种方法有个缺陷就是当有新数据加入时，可能导致max和min的变化，需要重新定义。不适合距离度量的场景，比如knn这种算法。
• 另外，这种方法对于outlier非常敏感，影响了max或min值，使得规范化后的值相近且均接近0。所以这种方法只适用于数据在一个范围内分布的情况。

#max-min标准化
minmax_scaler=preprocessing.MinMaxScaler()      #建立MinMaxScaler模型对象
data_scale_2=minmax_scaler.fit_transform(data)  #MinMax标准化处理

4.1.1.4 MaxAbs

MaxAbs：最大值绝对值标准化，和MaxMin方法类似，将数据落入一定的区间[-1,1]，但是MaxAbs具有不破坏数据结构的特点，可以用于稀疏数据，稀疏的CSR或CSC矩阵。（为矩阵的两种储存格式）。转换函数为:x’=x/|max|。

#MaxAbscaler标准化
maxab_scaler=preprocessing.MaxAbsScaler()          #建立MaxAbsScaler对象
data_scale_3=maxab_scaler.fit_transform(data)      #MaxAbScaler标准化处理

4.1.1.5 RobustScaler

RobustScaler：在某些情况下，假如数据中有离群点，我们使用均值和方差缩放，可能并不是一个很好的选择，因为异常点的特征往往在标准化后容易失去离群特征，此时就可以用RobustScaler 针对离群点做标准化处理。此方法对数据中心和数据范围有鲁棒性的估计。
这种方法去除了中位数并根据四分位距离(也就是说排除了离群值)，对数据进行标准化。即使用第一分位数到第三分位数之间的数据产生均值和标准差，然后做z-score标准化。

#RobustScaler标准化
robustscaler=preprocessing.RobustScaler()      #建立MaxAbsScaler对象
data_scale_4=robustscaler.fit_transform(data)  #MaxAbScaler标准化处理

各种处理方式的对比图：

4.1.1.6 关于[-1,1]和[0,1]

假设我们有一个只有一个hidden layer的多层感知机（MLP）的分类问题。每个hidden unit表示一个超平面，每个超平面是一个分类边界。参数w（weight）决定超平面的方向，参数b（bias）决定超平面离原点的距离。如果b是一些小的随机参数（事实上，b确实被初始化为很小的随机参数），那么所有的超平面都几乎穿过原点。所以，如果data没有中心化在原点周围，那么这个超平面可能没有穿过这些data，也就是说，这些data都在超平面的一侧。这样的话，局部极小点（local minima）很有可能出现。 所以，在这种情况下，标准化到[-1, 1]比[0, 1]更好。

1. 在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候，StandardScaler表现更好。

2. 在不涉及距离度量、协方差计算、数据不符合正太分布的时候，可以使用MinMaxScaler。比如图像处理中，将RGB图像转换为灰度图像后将其值限定在[0 255]的范围。
   原因是使用MinMaxScaler，其协方差产生了倍数值的缩放，因此这种方式无法消除量纲对方差、协方差的影响，对PCA分析影响巨大；同时，由于量纲的存在，使用不同的量纲、距离的计算结果会不同。
   而在StandardScaler中，新的数据由于对方差进行了归一化，这时候每个维度的量纲其实已经等价了，每个维度都服从均值为0、方差1的正态分布，在计算距离的时候，每个维度都是去量纲化的，避免了不同量纲的选取对距离计算产生的巨大影响。

4.1.2 数据变换

通过以上对数据标准化的说明可知，当数据为正态分布时，再进行处理的效果是很好的。但实际中我们遇到的数据大多都是非正态的，如果能把非正态数据转为状态数据，那么处理的结果将会更加准确。以下有三种转换方法，可以把非正态数据转为正态分布的数据。

1. 对指化
   对指化，即对数化和指数化。由于对数和指数的特点，可以把有些有偏数据转为正态分布的数据。右偏数据取对数，左偏数据取指数，减小较大值与较小值之间的差距。取对数的原因如下：
   1. 缩小数据范围。有时候变量数据很大，计算时可能超过计算机默认的取值范围。
   2. 可以讲乘法转换为加法。如对数收益率的可加性。
   3. 压缩变量尺度使数据更平稳，消除异方差。稳定方差，始终保持分布接近于正态分布并使得数据与分布的平均值无关。
   4. 取对数后回归得到的系数正好是经济学中弹性的定义。
   5. 数据存在负数时不能直接取对数，应该先对数据进行适当的平移后再取对数。
   6. 一般是对水平量数据取对数，而不是比例数据，如变化率等。
      为什么进行指数化
      建模时数据为什么要取对数？
      log1p和expm1
      注：由于两者是互相的反向操作。因此对数据进行转换后，记得要把数据转换回来。
2. Box-Cox转换
   其本质上是指数化，对数化。通过计算λ值，得出最佳的调整系数，进行转换。
   box-cox转换说明

from scipy.stats import boxcox
trains.SalePrice,lambda_=boxcox(trains.SalePrice)

from scipy.stats import boxcox_normmax
from scipy.special import boxcox1p
lambda_2=boxcox_normmax(trains.SalePrice+1)
print(lambda_2)
trains.SalePrice=boxcox1p(trains.SalePrice,lambda_2)

使用boxcox1p()可使数据的峰度变得更小，但偏度没有boxcox()的结果小。

4.1.2 二值化

定量特征的二值化的核心在于设定一个阈值，小于等于阈值的赋值为0，大于阈值的赋值为1，公式表达如下：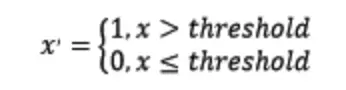

这种处理是对连续数据进行分组，但二值化用的比较少，一般是对数据进行多组的离散化处理。在数据探索性分析中有过描述，这里不再赘述。

from sklearn.preprocessing import Binarizer
# 二值化，阈值为3，返回值为二值化后的数据,参数threshold表示小于等于3的数表示为0，大于0.0的数据表示为1
Binarizer(threshold=3).fit_transform(iris.data)

4.1.3 数字特征构建

关于数字特征的构建可以从以下两个方面考虑：

1. 如果我们知道各个特征的具体含义，我们可以根据其含义来构造新特征，同时适当抛弃一些旧特征。比如金融类数据中利润=成本-支出。我们就可以构造一个利润特征。一般数字特征构建通过加减乘数四则运算。
2. 如果我们不知道各个特征的具体含义，我们可以用多项式变换构造一系列特征。构造后的特征我们再使用特征选择方法挑选出对模型贡献大的特征，其余特征抛弃。多用于去敏数据。
   常见的就是二项式变换:
   假如一个输入样本是２维的，形式如[a,b]，则多项式变换后的特征有（其实就是（a+b）*（a+b）的每一项加上原始的a和b）:a，b，a平方，b平方，2ab。更多项的多项式变换也类似。

from sklearn.preprocessing import PolynomialFeatures

#多项式转换
#参数degree为度，默认值为2
PolynomialFeatures().fit_transform(iris.data)

4.2 分类和有序特征的处理和构建

4.2.1 标签编码

有时我们得到的数据，不是数字型的，比如船舱等级ABC，受教育程度小学，中学，高中，性别中的男女等，这时无法直接将其放入模型中进行处理，因此我们需要将其转为123这种数字型。说白了就是替换。
sklearn中LabelEncoder可以将标签分配一个0—n_classes-1之间的编码。
pandas也有同样的函数。

还有一种替换方式为，根据字符出现的频率/频数，对原始数据进行替换。比如，性别这个数据中，男的出现频数为60，女的出现频数为40.那么久可以用60和40区替换男女，或者用频率去替代，这样相当于直接对数据进行了缩放。

但是这样得到的数据，也不能直接放入模型中，因为1,2,3之间对计算机来说是有具体大小的，而我们将其转为1,2,3，是为了让计算机能够处理这类数据。这样的连续输入，估计器会认为类别之间是有序的，但实际却是无序的。人对数字的理解跟计算机不一样。如下图，左边的结果并不是我们想要的。因此，还需要进行下一步，将数据“打散”。

4.2.2 独热编码

将离散特征通过one-hot编码映射到欧式空间，是因为，在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。类别型数据变为one_hot编码时，对于一个有k个取值的类别型特征，我们只需要k-1列one_hot编码就可以表示所有取值。

• one-hot编码为什么可以解决类别型数据的离散值问题
  首先，one-hot编码是N位状态寄存器为N个状态进行编码的方式
  eg：高、中、低不可分，用0 0 0 三位编码之后变得可分了，并且成为互相独立的事件。类似 SVM中，原本线性不可分的特征，经过project之后到高维之后变得可分了（核方法）。GBDT处理高维稀疏矩阵的时候效果并不好，即使是低维的稀疏矩阵也未必比SVM好。
  对于每一个特征，如果它有m个可能值，那么经过独热编码后，就变成了m个二元特征（如成绩这个特征有好，中，差变成one-hot就是100, 010, 001）。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。
  这样做的好处主要有：

  1. 解决了分类器不好处理属性数据的问题
  2. 在一定程度上也起到了扩充特征的作用

• 使用one-hot编码的例子
  比如，有一个离散型特征，代表工作类型，该离散型特征，共有三个取值，不使用one-hot编码，其表示分别是x_1 = (1), x_2 = (2), x_3 = (3)。两个工作之间的距离是，(x_1, x_2) = 1, d(x_2, x_3) = 1, d(x_1, x_3) = 2。那么x_1和x_3工作之间就越不相似吗？
  显然这样的表示，计算出来的特征的距离是不合理。那如果使用one-hot编码，则得到x_1 = (1, 0, 0), x_2 = (0, 1, 0), x_3 = (0, 0, 1)，那么两个工作之间的距离就都是sqrt(2).即每两个工作之间的距离是一样的，显得更合理。离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。

• 对多个类别使用one-hot编码更为合理
  将离散型特征进行one-hot编码的作用，是为了让距离计算更合理，但如果特征是离散的，并且不用one-hot编码就可以很合理的计算出距离，那么就没必要进行one-hot编码，比如，该离散特征共有1000个取值，我们分成两组，分别是400和600,两个小组之间的距离有合适的定义，组内的距离也有合适的定义，那就没必要用one-hot 编码。

• 树模型不太需要one-hot编码
  对于决策树来说，one-hot的本质是增加树的深度
  tree-model是在动态的过程中生成类似 One-Hot + Feature Crossing 的机制
  1.一个特征或者多个特征最终转换成一个叶子节点作为编码 ，one-hot可以理解成三个独立事件
  2.决策树是没有特征大小的概念的，只有特征处于他分布的哪一部分的概念
  one-hot可以解决线性可分问题 但是比不上label econding
  one-hot降维后的缺点： 降维前可以交叉的降维后可能变得不能交叉
  独热编码

注：对于类别型数据我们需要先观察其对于模型的贡献大不大，而不是全部变为one_hot编码。假如一个类别型数据有大量取值，但每个取值占总样本数的比例都很小（如5%以下），那么这个类别型数据进行one_hot编码化后每一列one_hot编码特征的方差都很小，对于模型的贡献极其有限。因此这个类别特征我们选择直接删除而不变为one_hot编码。

from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder()
enc.fit([[0,0,3],[1,1,0],[0,2,1],[1,0,2]])
enc.transform([[0, 1, 3]]).toarray()
array([[1., 0., 0., 1., 0., 0., 0., 0., 1.]])

说明：fit了4个数据3个特征，而transform了1个数据3个特征。第一个特征两种值(0: 10, 1: 01)，第二个特征三种值(0: 100, 1: 010, 2: 001)，第三个特征四种值(0: 1000, 1: 0100, 2: 0010, 3: 0001)。所以转换[0, 1, 3]为[ 1., 0., 0., 1., 0., 0., 0., 0., 1.]。

4.2.2 特征构建

关于类别特征的构建主要是用“相乘”。比如下面这个例子。通过pclass和sex通过相乘，得到新的特征，pclass=3的且sex=male的，把数据拆分得更细致。

4.4 时间特征的处理和构建

4.4.1 时间特征的处理

当我们拿到数据后，发现有时间特征，首先要做的就是把数据类型进行转换，因为大多数情况下，原始数据中的类型为object，我们需要转为datetime。可以用pandas中的to_datetime或者astype。转换代码to_datetime可以调整时间格式。

pd.to_datetime(pd.Series(['05/23/2005']))
2005-05-23 00:00:00
dtype: datetime64[ns]

pd.to_datetime(pd.Series(['05/23/2005']), format="%m/%d/%Y")
2005-05-23
dtype: datetime64[ns]

df['date'] = df['date'].astype('datetime64[ns]')
print(type(df_launath['date'].iloc[0]))
<class 'pandas._libs.tslib.Timestamp'># 时间戳格式

数据类型转换，注意其中error的应用，如果转换不过来，说明数据内有的数据不属于datetime类型，需要进行清洗后，再做应用。

4.4.2 时间特征的构建

关于时间特征的构建主要有以下三种方法：
1.时间信息提取。比如年月日，季度，周数，周几，小时分钟秒等。
2. 距离某一时刻过去了多久。比如，日期是否为节日，或者距离节日还有多少天，过了多少天等。

3. 时间差。时间1减去时间2


另外，也可以对时间序列数据进行one-hot编码。对于类似年-月-日形式的时间型特征，我们需要先将其变为三列年、月、日特征。然后观察我们的数据集标签与这三列特征有无线性关系，如果有，那么保留这些特征，转成one_hot编码；如果没有什么显著的关系，先保留。

4.5 文本特征的处理和构建

文本特征处理方法包括两个方面：词袋模型和词向量。由于本人对文本挖掘的知识了解过少，这里仅简单介绍下一些处理的方式。以后学了再补……

4.5.1 词袋模型

1. 词袋：文本数据预处理后，去掉停用词，剩下的词组成的list，在词库中的映射稀疏向量。Python中用CountVectorizer处理词袋。
   
2. 把词袋中的词扩充到n-gram：n-gram代表n个词的组合。比如“我喜欢你”、“你喜欢我”这两句话如果用词袋表示的话，分词后包含相同的三个词，组成一样的向量：“我 喜欢 你”。显然两句话不是同一个意思，用n-gram可以解决这个问题。如果用2-gram，那么“我喜欢你”的向量中会加上“我喜欢”和“喜欢你”，“你喜欢我”的向量中会加上“你喜欢”和“喜欢我”。这样就区分开来了。
   
3. 使用TF-IDF特征：TF-IDF是一种统计方法，用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加，但同时会随着它在语料库中出现的频率成反比下降。TF(t) = (词t在当前文中出现次数) / (t在全部文档中出现次数)，IDF(t) = ln(总文档数/ 含t的文档数)，TF-IDF权重 = TF(t) * IDF(t)。自然语言处理中经常会用到。
   
   TF：
   

IDF：

文字内容转自文本数据的简单处理

4.5.2 文本处理步骤

文本处理步骤主要有以下四步：文本大小写，词形还原，词干，停用词。

1. 大小写问题
   这个就是统一标准。好像sklearn中的文本处理的包可以自动忽略大小写的问题。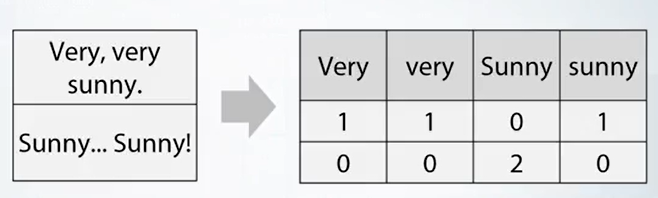
   
2. 词形还原，词干
   把词进行还原，比如going,went等转为go。词干，把握词最重要的部分，其他舍去。
   
3. 停用词
   比如a,this,the等常见的用语，可能在句子中并没有实际的意义，处理时将其删除。简化数据。
   

4.5.3 词向量

词向量是把词映射到向量的表示形式，word2vec。把文本转为向量，比较相似度（相似度一般用余弦定理）。

由于本人对文本挖掘了解，无法做过多的说明。这里贴上两篇文章，供参考学习。
通俗理解word2vec
小白都能理解的通俗易懂word2vec详解

五、总结

特征处理中sklearn的类。

以上是特征处理和特征生成相关的知识介绍。这块是数据挖掘的重中之重，数据处理的好坏和特征生成的优良直接影响模型的精度。
这篇文章是本人按照自己的理解和网上查阅相关资料写成的，其中难免会有错误的地方或者没有提到的处理方法，欢迎大家进行指正。如果这篇文章对您有帮助的话，也希望您能点赞关注下，后续会把特征工程写完，并且还有模型原理和模型评估的内容。

六、参考文献

特征工程的代码实现
https://www.cnblogs.com/jasonfreak/p/5448385.html
https://blog.csdn.net/Dream_angel_Z/article/details/49388733
https://blog.csdn.net/weixin_44327656/article/details/90180468
https://blog.csdn.net/zgcr654321/article/details/88419585
https://www.cnblogs.com/bjwu/p/8977141.html
https://blog.csdn.net/weixin_37536446/article/details/81435461