C. Good Subarrays（思维+前缀和）好题啊

codeforces Educational Codeforces Round 93 (Rated for Div. 2)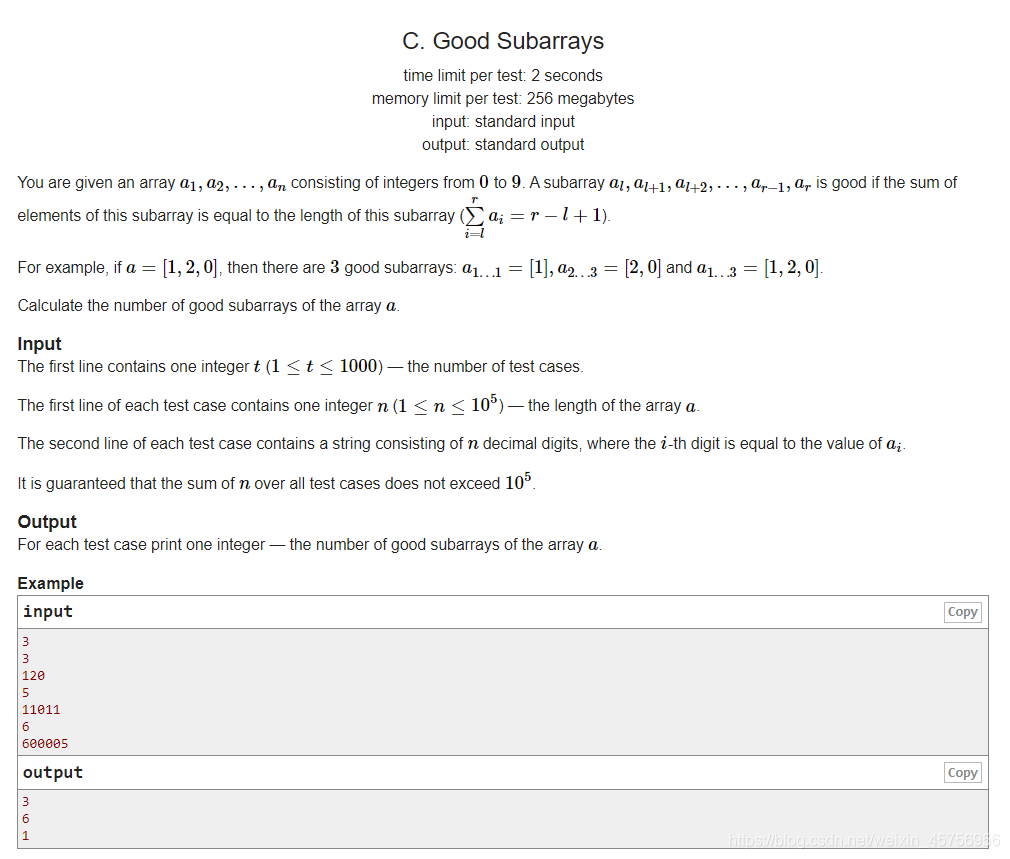

题意：求n长度数组中区间和和为区间长度的区间个数。
思路分析：首先想到用前缀和优化，如果直接前缀和判断每一个区间，时间复杂度为O(n*n),果不其然超时了。如果我们将数组中所有元素都-1，那么问题就简单了不少，符合条件的区间和为0。问题转换为求区间和为0的区间个数，就可以开始整活了。
我们首先维护一个map<int,int> M;
M[sum[i]]表示目前第i个元素为止前缀和为sum[i]出现的次数（不含第i个）。
众所周知，和为0的区间，减去和为0的区间，就可以找到一个和为0的新区间。（类似于集合运算的A-B）
同理可得，和为x的区间，减去区间和为x的区间，也是一个和为0的新区间。
综上所述，我们只需遍历一遍前缀和sum[i],如果sum[i]为0，ans++。再加上 前i-1个元素前缀和为当前sum[i]的个数，就是最终答案。
最终结论，这是一道好题，我还是太菜了。
ac代码：

#include<iostream>
#include<map> 
using namespace std;
const int N=1e5+5;
typedef long long ll;
ll a[N];
ll sum[N];
int main()
{
	int t;cin>>t;
	while(t--)
	{
		map<int,int>m;
		ll ans=0;
		int n;cin>>n;
		string s;cin>>s;
		for(int i=1;i<=n;i++)
		a[i]=s[i-1]-'0'-1;//转换和元素-1
		for(int i=1;i<=n;i++)
		sum[i]=sum[i-1]+a[i];//前缀和
		for(int i=1;i<=n;i++)
		{
			if(sum[i]==0)ans++;
			ans+=m[sum[i]];
			m[sum[i]]++;
		}
		cout<<ans<<endl;
	}
	return 0;
}