目标检测（损失函数）：目标定位损失—GIoU

- - 1、提出问题
  - 2、解决方案

C V P R 2019

有一篇介绍目标检测定位损失函数的

p a p e r

：

论文链接：Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression

1、提出问题

目标检测的主要任务之一是对目标定位。通常我们使用边界框来表示它。衡量目标检测定位性能的主要指标是交并比 $I o U$ 。但是我们在设计损失函数时通常使用 $m s e$ 等损失函数来优化模型对目标的定位结果。但是，这类损失函数并不总是能够很好地反映定位精度。如下图 $1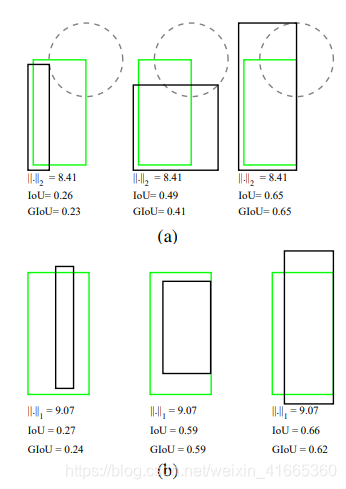$ 所示：
在这里插入图片描述

图 1: (a) $l_2$ 距离相等但是 $I o U$ 和 $G I o U$ 不相等；(b) $l_1$ 距离相等但是 $I o U$ 和 $G I o U$ 不相等

因此，考虑直接使用 $I o U$ 衡量目标定位损失。
$L_{IoU}=1-IoU$

$I o U$ 还有一个优点：尺度不变性

但是这样做也存在以下几点问题：

如果两个框没有相交，则 $I o U = 0$ 这时无法反映两个框的距离（相似程度）。并且损失函数此时不存在梯度，无法通过梯度下降进行训练。
即使相同的 $I o U$ 也不能代表检测框的定位效果相同。如图所示：
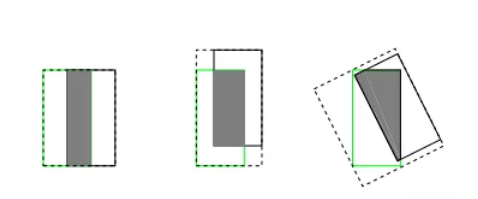
图 2: 以上几种情况下均有 $I o U = 0.33$ 但是显然从左到右定位效果越来越差。

2、解决方案

针对上述两个缺陷，作者提出新的指标： $G I o U$ ，计算方法如图 $3$ 所示。
在这里插入图片描述

图 3: $G I o U$ 计算方法

算法思路如下：
输入：任意两个凸几何
输出： $G I o U$
对于 $A$ 和 $B$ 首先计算最小闭包 $C$ 。
$IoU=\frac{|A\cap B|}{|A\cup B|}$
$\ ( A ∪ B ) ∣ ∣ C ∣ GIoU=IoU-\frac{|C\backslash(A\cup B)|}{|C|}$

$G I o U$ 具有如下特点：

$L_{GIoU}=1-GIoU$ 损失函数具有一般损失函数所有的性质，如，非负性。
对尺度不敏感，即尺度不变性。
$G I o U$ 是 $I o U$ 的一个下界，当两个几何越相似，该下界越紧。即， $\lim _{A \rightarrow B} GIoU(A, B)=IoU(A, B)$ 。
$\forall A, B \subseteq \mathbb{S}, 0 \leq IoU(A, B) \leq 1$ ，但是， $\forall A, B \subseteq \mathbb{S}, -1 \leq GIoU(A, B) \leq 1$
与 $I o U$ 只关注重叠区域不同， $G I o U$ 不仅关注重叠区域，还关注非重合区域，能更好的反映两者的重合度。

损失函数计算步骤如下图 $4$ ：
在这里插入图片描述

图 4: $L_{IoU}$ 和 $L_{GIoU}$ 计算方法

原文链接：https://blog.csdn.net/weixin_41665360/article/details/100126744