因子分析

跟主成分分析对比

• 主成分分析：

  • 主成分是各指标的线性组合
  • 选取主要的几个主成分包含了原始数据80%以上的信息
  • 实现降维

• 因子分析

  • 因子的线性组合构成原始变量（指标）
  • 每个指标有一个特殊因子。
  • 让特殊因子尽可能小，比如公共因子解释90%，特殊因子解释10%。就像回归分析的残差

• 主成分分析只是一个计算，也不需要构造模型

• 而因子分析是自己构造模型，模型随着我们需要的因子个数改变

• 因子分析有许多假定

• 因子分析比主成分分析好，在建模中优先用因子分析

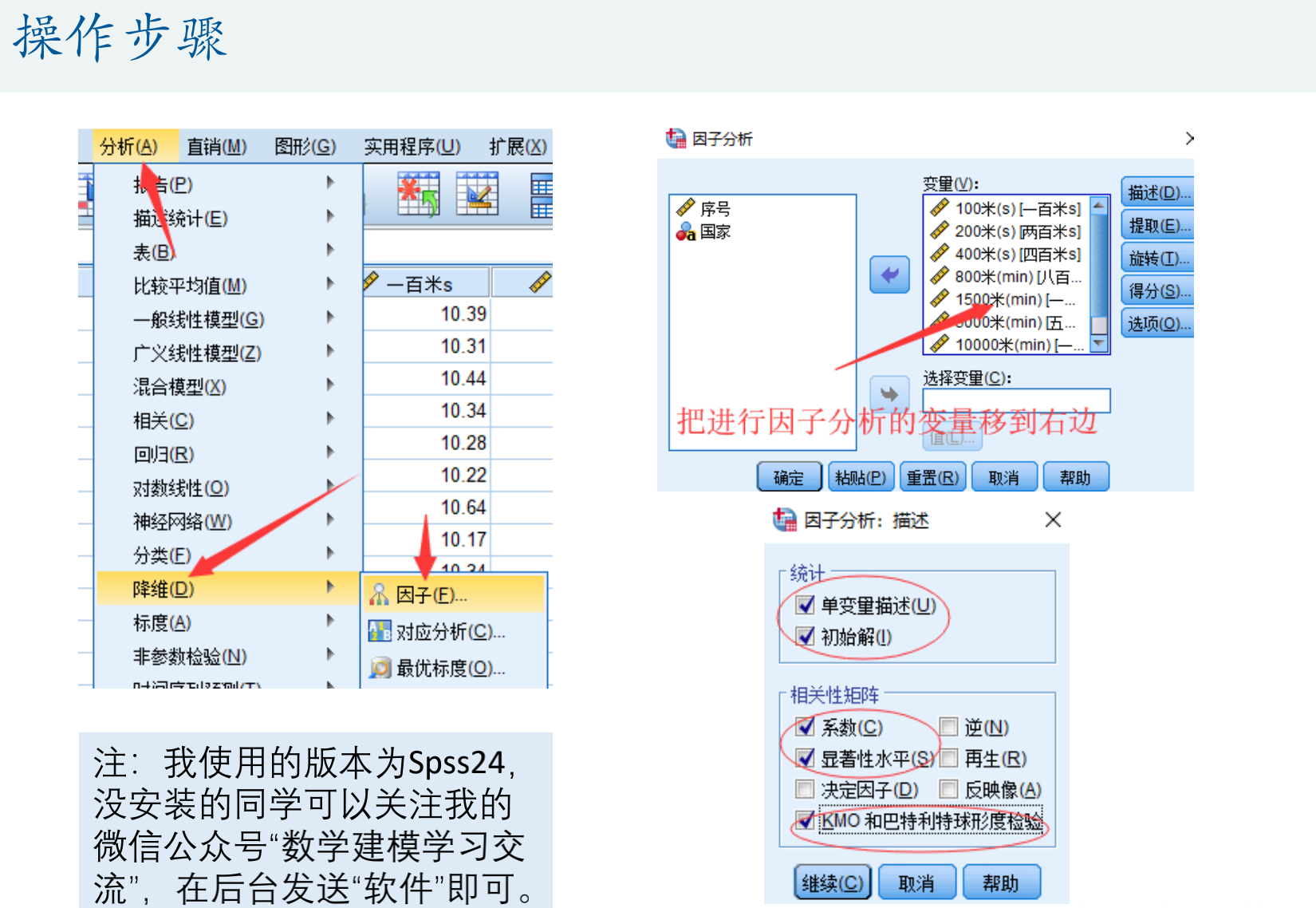
因子分析的实例

例1

• 对十个指标进行降维

例2

因子分析模型

原理

• u是均值
• 公共因子可以看作是每个原始变量共同拥有的某些特征
• 特殊因子可以理解为只影响这个指标的因子

用矩阵形式表现

• A是系数矩阵，也称为因子载荷矩阵
• 一般m<=p，公共因子个数小于原始变量个数，要降维嘛
• 一个重要假定：A（p*m矩阵）的秩为m，用回归的说法就是保证了没有完全多重共线性。求出来的系数是有效的
• 要因子分析，就是要求A这个矩阵

假设

求A，要进行一些假设

• 公共因子均值为0
• 公共因子协方差矩阵是单位矩阵
  • 说明公共因子彼此之间是不相关的，且具有单位方差
• 特殊因子协方差矩阵是一个对角矩阵
• 公共因子与特殊因子不相关
  • 类似回归里的变量不具有内生性，内生性会导致估计出来的结果失效，没有一致性
• 通过假设我们可以通过某种方法求出A

性质

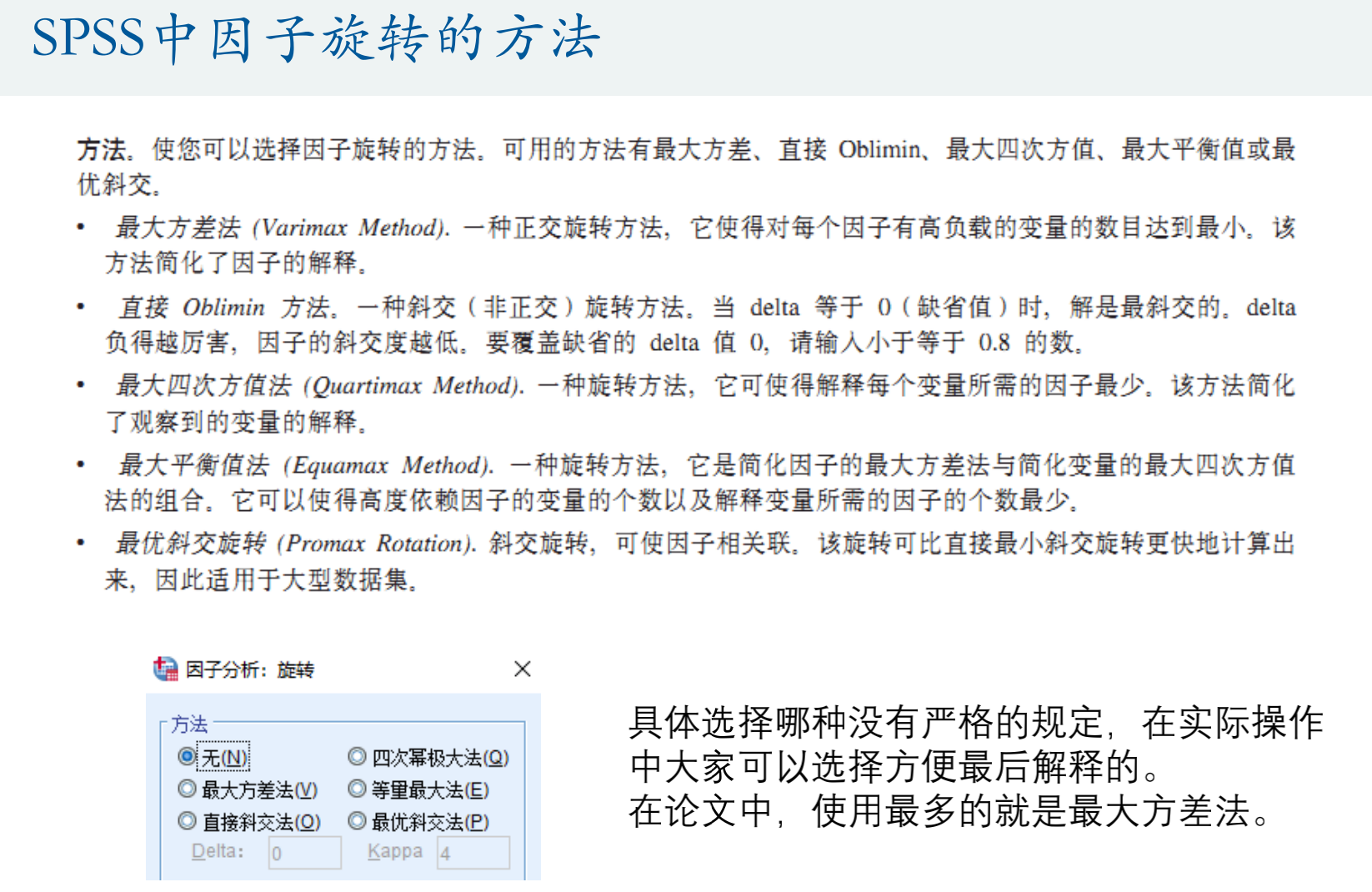
• 分解协方差矩阵

x的均值就是u

协方差矩阵的定义：

x-u变为Af+e，展开，每一项与假设结合处理

最后原始变量的协方差矩阵分解，等于A乘A转置，加上特殊因子的协方差矩阵

• 证明因子载荷矩阵不唯一

• 正交矩阵就是自己乘自己转置为单位矩阵
• 人为构造A*,f*发现仍然成立，说明只要乘一个正交矩阵，因子载荷矩阵不唯一
• 所以可以找到一个我们便于解释的因子载荷矩阵。可以通过乘一个特殊的正交矩阵的方式，相当于进行了一次旋转。我们称为因子旋转

因子载荷矩阵的意义

• $a_{ij}$
  • 原始变量$x_i$与公因子$f_i$的协方差
  • x标准化后就是相关系数
  • 默认经过了标准化
  • 证明也不是很难

• 行元素平方和$h_i^2$

  • 原始变量$x_i$对公因子的依赖程度

• $h_i^2$是公因子对$x_i$的影响，称为共性方差

• ${\sigma }_i^2$是特殊因子的方差，称为个性方差

• 由于标准化之后的$x_i$方差为1，所以$h_i^2+{\sigma }_i^2$为1

• 作用：如果$h_i^2$为0.9，就可以说明公因子解释了90%，特殊因子解释了10%

• 列元素平方和$g_i^2$
  • 反应公因子$f_i$对x的贡献
• 到时候SPSS会把这些都跑出来
• 这一块是写论文，跑出来的结果怎么解释的关键

参数估计

• 主成分、最大似然估计、主轴因子法用的比较多
• 数学建模时可以都试一下，看一下哪个更方便自己解释，就选哪个

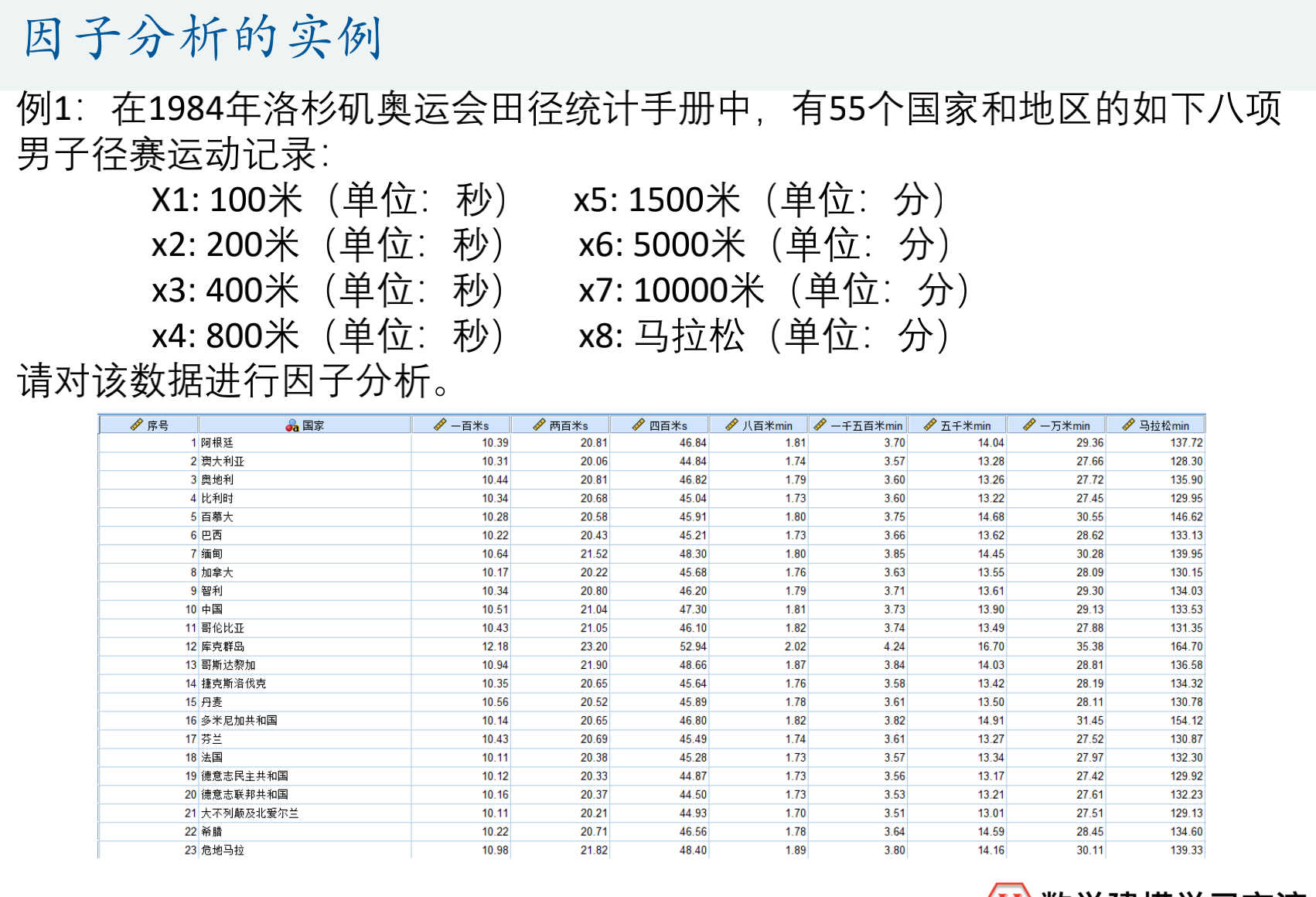
因子旋转方法

• 比赛时用正交旋转一般就够了
• 要使得新公共因子载荷系数绝对值尽可能接近0或1
  • 方便解释公因子，定义公因子

• SPSS中因子旋转方法
  • 最多使用最大方差法就行

因子分析

• 将公共因子表示为原始变量的线性组合

• 看起来像主成分分析，其实不是的，因为我们对因子有很多假设，没有那么简单

• 因子得分实际上就是求公共因子，不要理解复杂了

• 论文中实际上用第三种计算得分方法，是在第二种方法上改进的

SPSS操作实例

具体的操作，比较实用

第一次运行

第一次运行因子分析的结果一般作为参考，首先我们要确定原始数据是否适合进行因子分析，即能否通过KMO检验和巴特利特球形检验。

• 导入数据

• 勾选相关的统计
  • 相关性矩阵包括系数、显著性水平、检验

• 其中KMO检验和巴特利特球形检验
  • KMO检验直接根据SPSS给出的KMO值判断
  • 巴特利特球形检验
    • 原假设为变量间不存在相关性
    • 如果P值<0.05，则拒绝原假设，说明可以做因子分析

• 继续操作

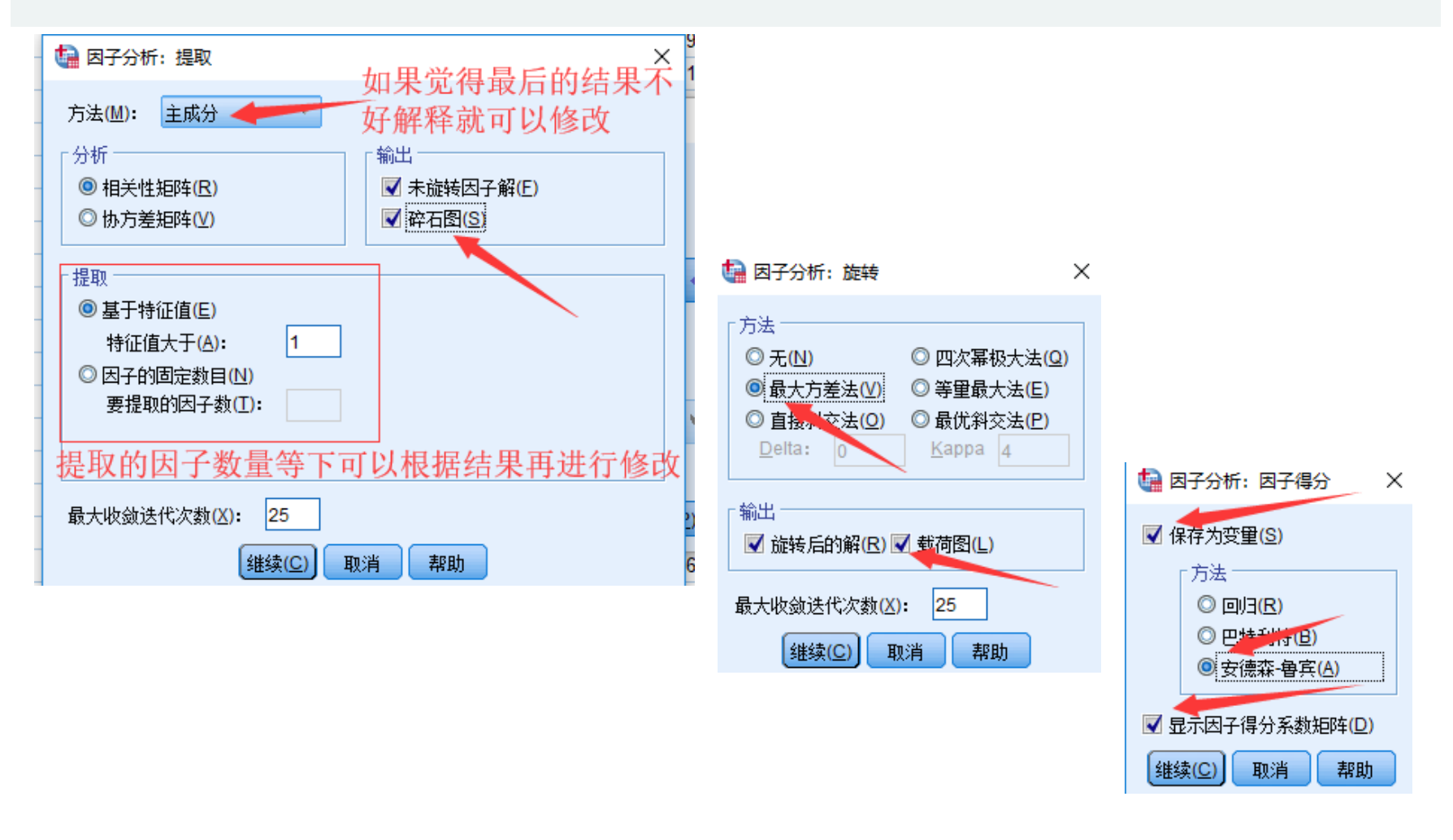
• 这里的主成分方法，如果不对得到的结果进行因子旋转，提取出来的因子跟主成分分析得到的主成分是一样的
• 提取的因子数，可以先不确定，先进行一次分析再确定，所以先勾选上面的基于特征值
• 因子分析一般会运行两遍
• 因子旋转方法
• 因子得分方法

结果分析，能否通过检验，说明一下

确定因子数量

• 跟主成分分析相似
• 后面越平坦说明信息越少
• 这个红框框可以在ppt画

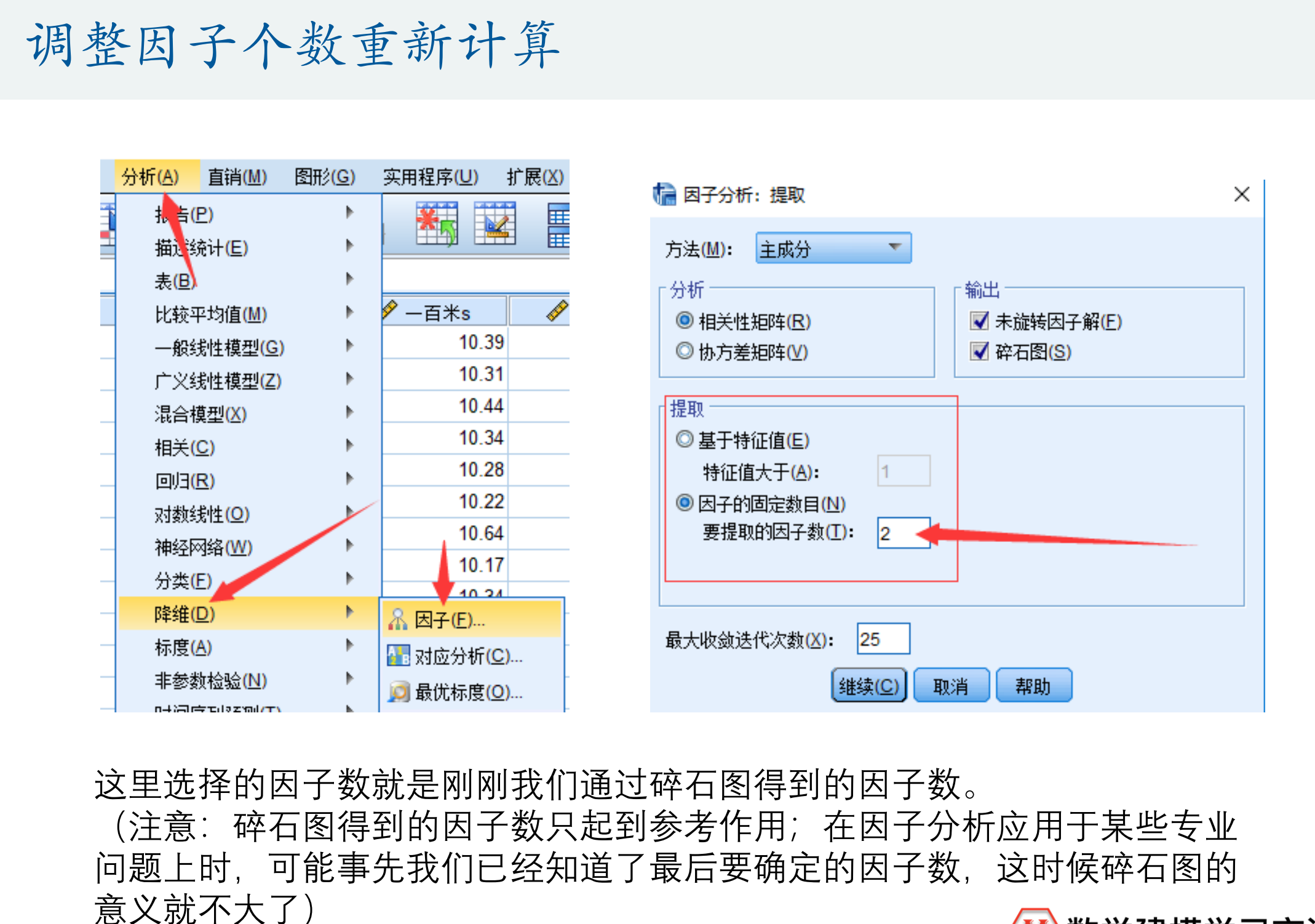
调整因子个数重新计算

对因子分析结果的介绍

• 共性方差

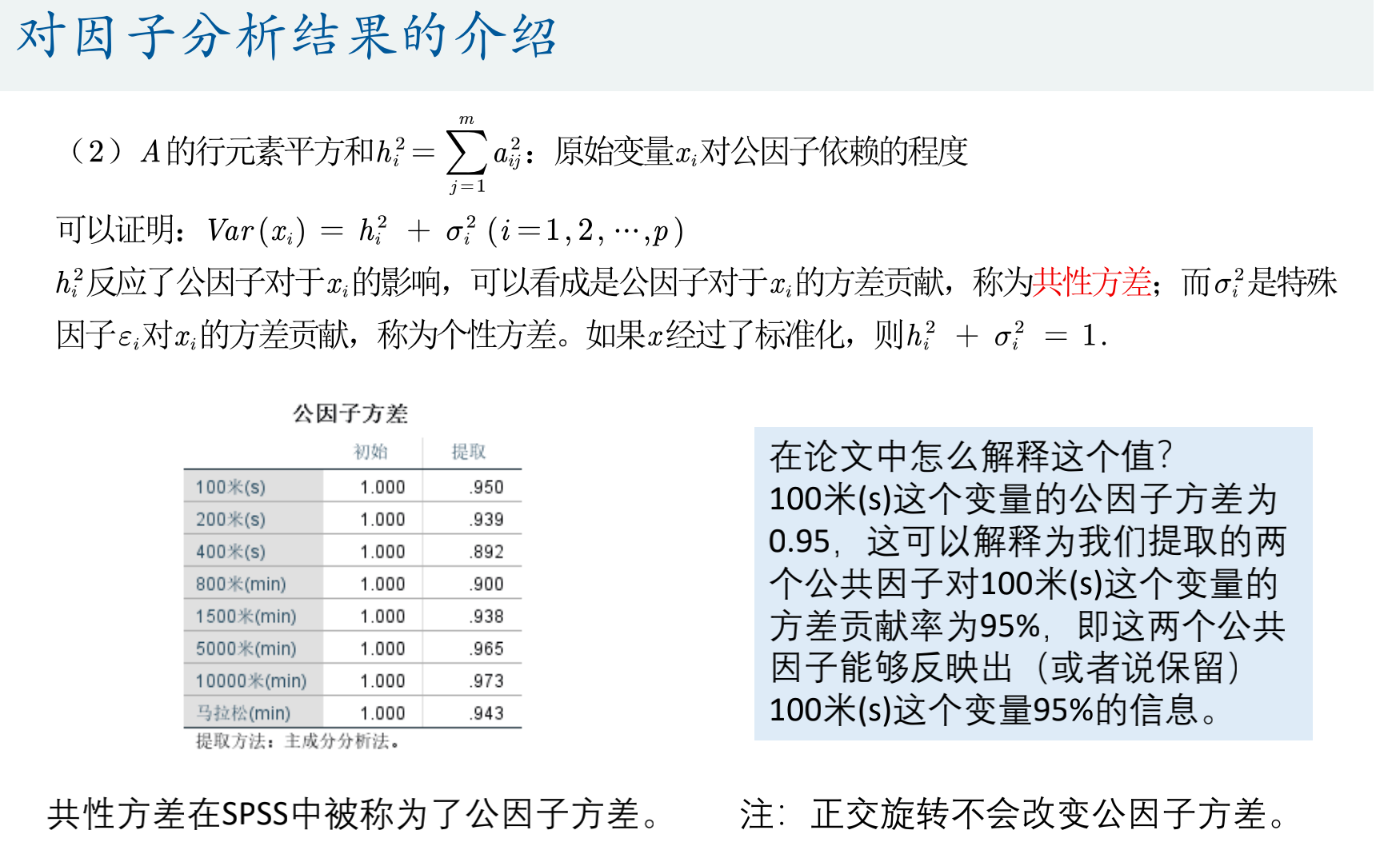
SPSS会默认标准化。

比如100m这里说明，提取的两个公共因子对这个100m的变量贡献率为95%

正交旋转不会改变公因子方差

• 总方差解释表
  • 旋转后的载荷平方和不会改变来及贡献率

• 成分矩阵
  • 成分矩阵就是没旋转的因子载荷矩阵
  • 这里明显可以看出旋转后的更好解释

• 有时候旋转后的也不是很好解释，那我们可以改变提取方法和旋转方法等
• 让结果好解释

因子载荷散点图

因子得分

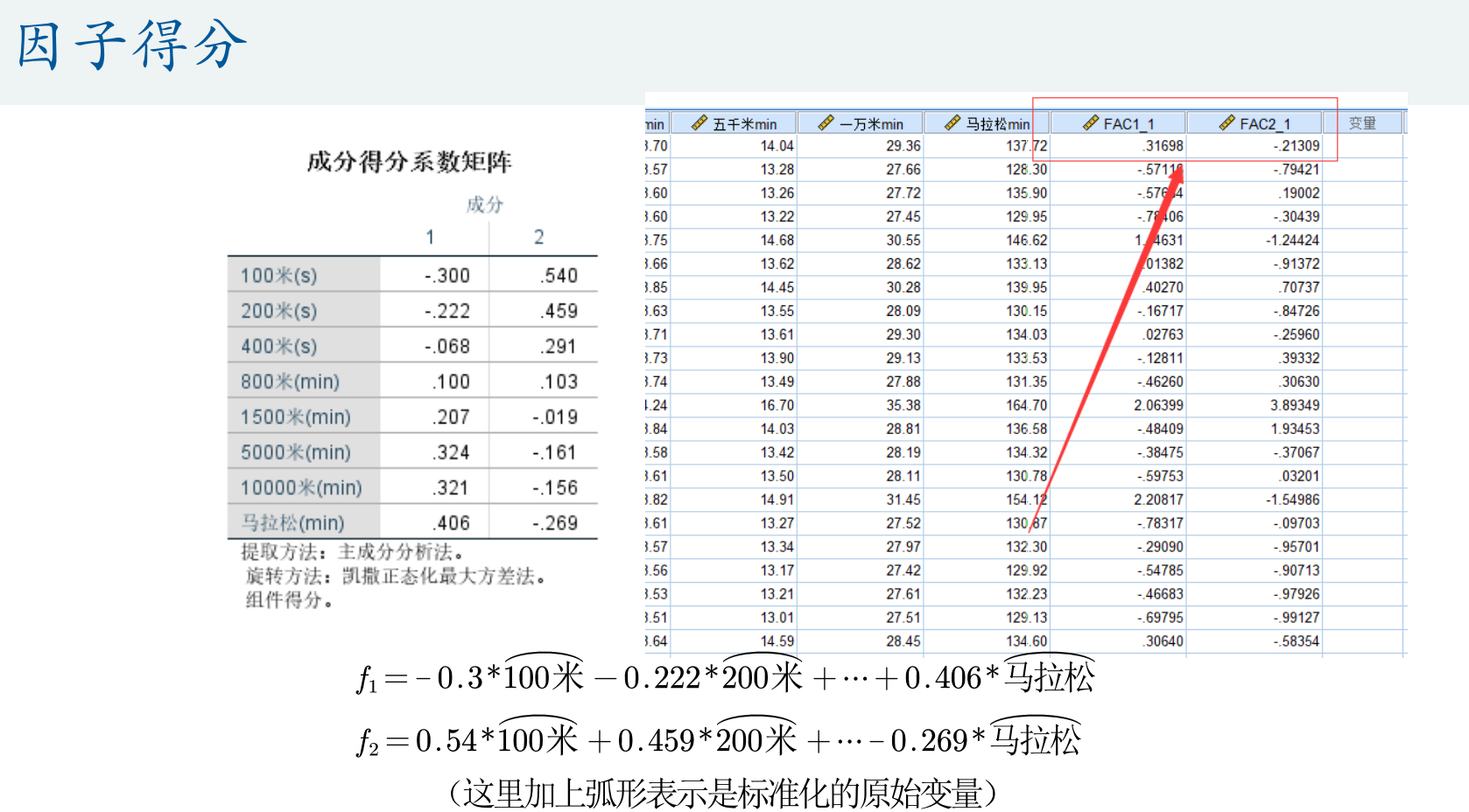
• 实现降维

• 不能用于评价，不能说明得分越高就越好

• 降维后可以用于聚类和回归

要将那两个检验写上去，当检验通过，说明指标间相关性较强，说明因子分析有效