数学表达

详细的数学表达还是建议看这里
马克科夫链是一个随机系统，必须满足两个条件：

• 系统任意时刻可以用有限个可能状态之一来描述
• 系统无后效性，即某阶段的状态一旦确定，则此后过程的演变不再受此前各种状态及决策的影响
  无后效性(附录有详细描述)

条件一 …… 概率向量(状态向量)

$X^{(n)} = (x_{1}^{(n)} \quad x_{2}^{(n)} \quad \dots \quad x_{k}^{(n)})^{T}$

• 概率向量的每个元素都是概率，并且元素之和为1。
• k是系统的可能状态数。
• $x_{i}^{(n)}$表示第n次观测时第i个状态的概率

这个概率向量$X^{(n)}$也被称为Markov的状态向量
$X^{0}$被称为马尔科夫链的初始状态

条件二 …… 转移概率矩阵

$P = \begin{pmatrix} p_{11} && p{12} && \dots && p{1k} \\ p_{21} && p{22} && \dots && p{2k} \\ \vdots && \vdots && \quad && \vdots \\ p_{k1} && p{k2} && \dots && p{kk} \\ \end{pmatrix}$

• $p_{ij} (i,j=1,2,\dots,k)$表示这次观测时状态为j，现在观测是状态为i的概率
• P矩阵元素非负
• 每一列的元素之和都为1

根据无后效性我们可以的到，$X^{(n+1)} = PX^{(n)}$, 进一步有
$\qquad \qquad \qquad \qquad X^{(n)} = P^{n}X^{(0)}$

例子

有一个大的汽车租赁公司，有三家门店，你租的时候可以选择任何一个门店，还的时候也可以选择任何一家门店， 从不同门店借出和归还的概率如下表:

归还\借出	1	2	3
1	0.5	0.3	0.3
2	0.2	0.1	0.6
3	0.3	0.6	0.1

问题: 一辆车出2号门店借出，公司前三次应该从哪家店找最快捷

那么初始状态$X^{(0)} = (0,1,0)^{T}$,转移矩阵

$P = \begin{pmatrix} 0.5 && 0.3 && 0.3 \\ 0.2 && 0.1 && 0.6 \\ 0.3 && 0.6 && 0.1 \\ \end{pmatrix}$

那么为：
$PX^{(0)} = X^{(1)} = (0.3, 0.1, 0.6)^{T}$
$X^{(2)} = (0.35, 0.43,0.21)^{T}$
$X^{(3)} = (0.324,0.239,0.384)^{T}$

所以第一次先从3号门店找，
第二次先从2号门店找
第三次先从3号门店找

这里感觉有些怪怪的,因为按理说第一次找在3号，第二次找在2号，那么第三次就一定去1号找，应该是我没理解X的内涵本质

附录

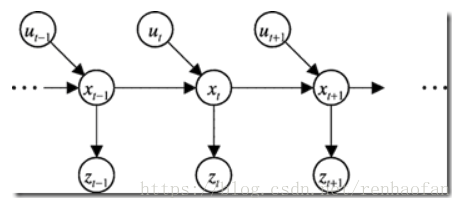
1. 马尔科夫假设的概率理解

t时刻的状态和t-1时刻和t时刻的动作决定。t时刻的观测仅仅同t时刻的状态相关

$$P(z_{t}|x_{0:t},z_{z:t},u_{1:t}) = P(z_{t}|x_{t}) \\ P(x_{t}|x_{1:t-1},z_{1:t},u_{1:t}) = P(x_{t}|x_{t-1},u_{t})$$

2. 参考

1. 线性代数 高等教育出报社
2. 微信公众号：红猴子
3. introduction to Markov chain by Waiyin Wong
4. （一）：细说贝叶斯滤波：Bayes filters