【树的遍历】重建二叉树（已知先序遍历和中序遍历构造一棵二叉树）

题意：

输入一棵二叉树前序遍历和中序遍历的结果，请重建该二叉树。

注意:

二叉树中每个节点的值都互不相同；
输入的前序遍历和中序遍历一定合法；
数据范围
树中节点数量范围 [0,100]。

样例

给定：
前序遍历是：[3, 9, 20, 15, 7]
中序遍历是：[9, 3, 15, 20, 7]

返回：[3, 9, 20, null, null, 15, 7, null, null, null, null]

返回的二叉树如下所示：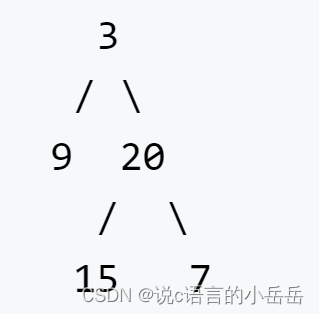

解题思路：

利用：
前序遍历（根左右）：根结点，左子树的前序遍历，右子树的中序遍历
可以知道根节点的值
中序遍历（左右根）：左子树的前序遍历，根节点，右子树的中序遍历
可以知道左子树的结点个数，右子树的结点个数，通过前序遍历中根节点的值在中序遍历中可以知道根节点的位置。

根节点：查找每个点在中序遍历中的位置
左子树：根据左子树的前序遍历和中序遍历递归创建
右子树：根据右子树的前序遍历和中序遍历递归创建

画图理解：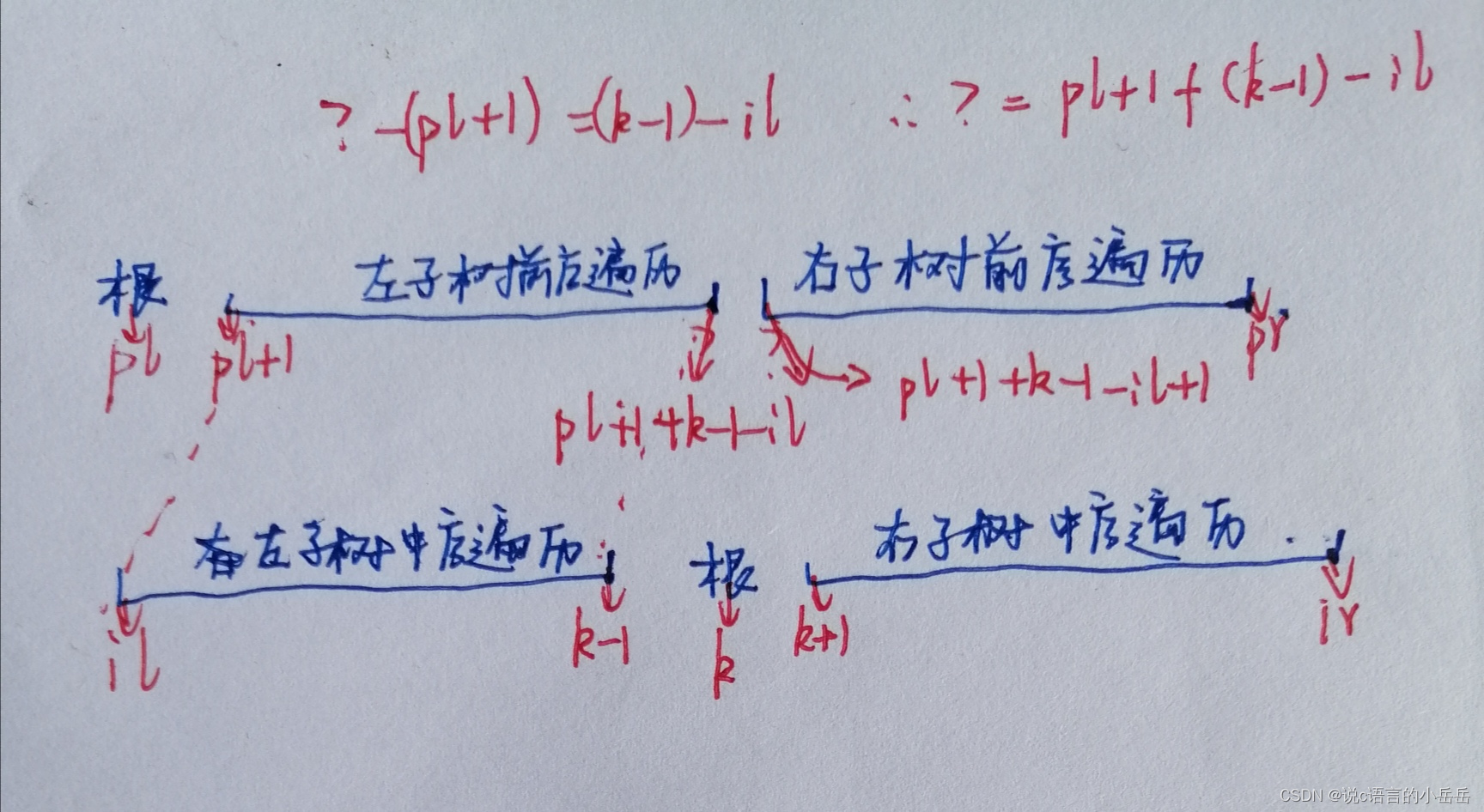

AC代码：

C++：

方法一：利用循环来查找

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:


    vector<int> preorder,inorder;//类似全局数组的作用，赋根节点的值时需要用到
    
    TreeNode *dfs(int pl,int pr,int il,int ir) //（前序遍历的起点，前序遍历的终点，中序遍历的起点，中序遍历的终点）
    {
        if(pl>pr) return NULL;  //递归终止条件
        
        auto root=new TreeNode(preorder[pl]);  //创建结点，把根节点值赋给当前结点
         
        //利用循环，查找根节点在中序遍历序列中的位置O(n)
        int k=-1;
        for(int i=il;i<=ir;i++){
            if(inorder[i]==root->val)
            {
                k=i;
            }
        }
        
        root->left=dfs(pl+1,pl+1+k-1-il,il,k-1);  //根据左子树的前序遍历和中序遍历递归创建左子树
        root->right=dfs(pl+1+k-1-il+1,pr,k+1,ir);//同理，根据右子树的前序遍历和中序遍历递归创建
        
        return root;//返回值是这个结点
        
    }
    
    
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder=_preorder,inorder=_inorder;
        
        
        return dfs(0,preorder.size()-1,0,inorder.size()-1);//递归创建树（前序遍历的起点，前序遍历的终点，中序遍历的起点，中序遍历的终点）
        
    }
};

方法二：利用哈希表来查找

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:

    unordered_map<int,int>hash;  //利用哈希表存储，查找时为O(1)
    vector<int> preorder,inorder;//类似全局数组的作用，赋根节点的值时需要用到
    
    TreeNode *dfs(int pl,int pr,int il,int ir) //（前序遍历的起点，前序遍历的终点，中序遍历的起点，中序遍历的终点）
    {
        if(pl>pr) return NULL;  //递归终止条件
        
        auto root=new TreeNode(preorder[pl]);  //创建结点，把根节点值赋给当前结点
         
        int k=hash[root->val];  //利用哈希表查找根节点在中序遍历序列中的位置
        
        root->left=dfs(pl+1,pl+1+k-1-il,il,k-1);  //根据左子树的前序遍历和中序遍历递归创建左子树
        root->right=dfs(pl+1+k-1-il+1,pr,k+1,ir);//同理，根据右子树的前序遍历和中序遍历递归创建
        
        return root;//返回值是这个结点
        
    }
    
    
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder=_preorder,inorder=_inorder;
        for(int i=0;i<inorder.size();i++)   hash[inorder[i]]=i; //存储每个点在中序遍历中的位置
        
        return dfs(0,preorder.size()-1,0,inorder.size()-1);//递归创建树（前序遍历的起点，前序遍历的终点，中序遍历的起点，中序遍历的终点）
        
    }
};

C语言：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
struct TreeNode* buildTree(int* preorder, int preorder_size, int* inorder, int inorder_size) {
    
    if(preorder==NULL || preorder_size==0||inorder==NULL||inorder_size==0)//判空
        return NULL;
        
    struct TreeNode *root =(struct TreeNode*)malloc(sizeof(struct TreeNode));//创建新节点
    
    root->val=preorder[0];//结点的值，根据先序遍历（根左右）可知是最左边的点
    int i;//记录退出循环后的i所在位置，即当前根节点的位置作为标记
    for(i=0;i<inorder_size;i++)
        if(inorder[i]==root->val)
            break;
    
    root->left=buildTree(&preorder[1],i,&inorder[0],i);//递归遍历左子树（左子树先序遍历序列的起点初始值，左子树先序遍历序列的长度，左子树中序遍历序列的起点初始值，左子树中序遍历序列的长度）
    root->right=buildTree(&preorder[i+1],preorder_size-i-1,&inorder[i+1],inorder_size-i-1);//递归遍历右子树（右子树先序遍历序列的起点初始值，右子树先序遍历序列的长度，右子树中序遍历序列的起点初始值，右子树中序遍历序列的长度）
    
    return root;
    
}