参考文章:https://blog.csdn.net/xyilu/article/details/9569063
特征工程参考文章:
https://www.cnblogs.com/infaraway/p/8645133.htmlwww.cnblogs.com主成分分析流程
主成分分析包含以下流程:
1、原始数据标准化。
2、计算标准化变量间的相关系数矩阵。
3、计算相关系数矩阵的特征值和特征向量。
4、计算主成分变量值。
5、统计结果分析,提取所需的主成分。
实例代码:
data Practice.PCA_Demo;
input num var1 var2 var3 var4;
cards;
1 21 10.7 99.7 9.5
2 9.5 17.9 139.6 18.7
3 21.2 8.4 90 6.8
4 12 22.7 42.5 24.1
5 6.8 21.2 55.2 22.4
6 8.2 22.4 55.6 22.6
7 3.6 29.2 68.3 26.7
8 19.5 15.2 18.8 17.4
9 24.8 5.4 43.7 2.9
10 8.4 18.6 146.2 19.7
11 28.9 4.4 4.9 1.1
12 19.5 15.1 10.2 18.5
13 28.3 4.7 13.3 1.8
14 24.7 12.1 116.8 12.6
15 12.8 23.6 90 23.7
16 23.1 6.8 100.1 3.7
17 15.1 13.7 100.9 14.2
18 2.9 6.2 80.7 2.7
19 18.4 11.8 99.3 13.8
20 22.9 12.3 47.6 13.3
21 5.8 29.4 83.5 27.6
22 18.8 8.6 61.1 8.9
;
run ;
主成分分析代码如下:
proc princomp
data = Practice.PCA_Demo
out = Work.PCA_Demo_out
prefix = comp
outstat = Work.PCA_Demo_stat
;
var var1 var2 var3 var4;
run ;
代码结果:
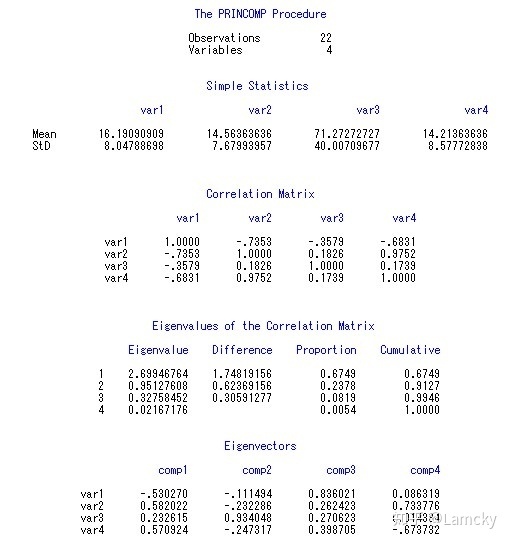
第4部分输出Eigenvalues of the Correlation Matrix,第四列Cumulative显示,第一个特征值分量占比0.6749(67.49%),第1、2个特征值合起来占比91.27%>85%,因此新变量comp1和comp2已经足以替代原有四个变量,它们是源数据集的主成分。
输出结果Work.PCA_Demo_out存放了原始数据集的所有变量以及新变量comp1、comp2、comp3和comp4,分别代表第1至第4主成分,它们对原始变量的解释力度依次减少。
附:
可以使用proc standard过程步来查看数据标准化的结果,代码如下:
proc standard
data = Practice.PCA_Demo
out = Work.PCA_Demo_std
mean = 0
std=1;
var var1 var2 var3 var4;
run ;
我们来验证一下主成分变量之间是否线性无关。使用proc corr过程步可以计算变量之间的相关系数,代码如下:
proc corr
data = Work.PCA_Demo_out
out = Work.PCA_Demo_Comp_Corr
;
var comp1-comp4;
with comp1-comp4;
run ;
可以使用proc corr过程计算相关系数,代码如下:
proc corr
data = Work.PCA_Demo_out
out = Work.PCA_Demo_Corr
;
var comp1-comp4;
with var1-var4;
run ;
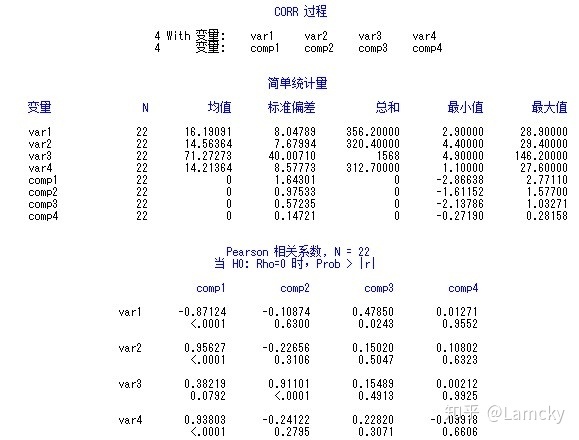
输出结果的第一行表示相关系数的值,第二行表示零假设下的检验概率。这些相关系数有其统计学名字,称为因子载荷量,反映了主成分变量受原始变量影响的程度,其绝对值越大,表示该主成分受该原始变量的影响越大,而值的符号则表示影响的方向。比如,comp1和var1的相关系数为-0.8712,检验概率<0.0001,在0.1水平上显著。
总结
以下概念很容易混淆,值得拎出来做一梳理:
原始变量之间的相关系数矩阵:可以看出原始变量之间的相关性。
原始变量和主成分变量之间的相关系数矩阵:可以看出主成分变量受原始变量影响的程度。
主成分变量之间的相关系数矩阵:主成分变量之间相关系数为零。
特征值:原始变量相关系数矩阵的特征值。
特征向量:原始变量相关系数矩阵的特征向量。