一、格兰杰因果关系定义
对于因变量,找到有助于预测的协变量。
"X is said to Granger-causeY if Y can be better predicted using the histories of bothX and Y than it can by using the history of Y alone."
二、格兰杰因果检验
格兰杰因果检验本质是对VAR模型的参数进行线性约束的检验(一般为检验系数是否为0),它使用Wald检验。Wald检验有效,建立在统计量服从渐进卡方分布的假设下。如果该假设被破坏,则Wald检验非有效,格兰杰检验也非有效。
那么在什么条件下假设会被破坏?比如某些变量是非平稳的;出现非线性约束时;预检验技术效力低...
在这之前,我们回到一般步骤:数据预检验+建模格兰杰检验
首先,数据预检验:单位根检验(ADF PP检验),协整检验(Johansen检验)
其次,建模和格兰杰检验:以下有三种情况
第一种情况:变量们都存在单位根(经济数据一般是一阶单位根,或者是在0~1之间的分数积整),且不存在协整关系,那么做一阶差分处理后,差分数据应用VAR建模,这样在对VAR系数进行检验时,传统渐进理论是有效的。
第二种情况:都存在单位根,存在协整关系,在水平数据(没有经过差分的数据)上应用ECM建模,再进行系数检验。
第三种情况:不管变量是否平稳,不管变量间是否存在协整关系,我们可以直接在水平数据上应用Wald检验来检验线性或非线性约束。这就是Toda Yamamoto 方法,简称TY-Granger方法。
TY方法保证了统计量服从渐进卡方分布,保证了格兰杰因果检验的有效性。
三、TY-granger方法步骤(E-Views)
1、单位根检验:确定积整阶数。尽量进行交叉检验。令变量中最大的积整阶数为m(一般m=1)。
2、确定最佳的VAR滞后阶数:
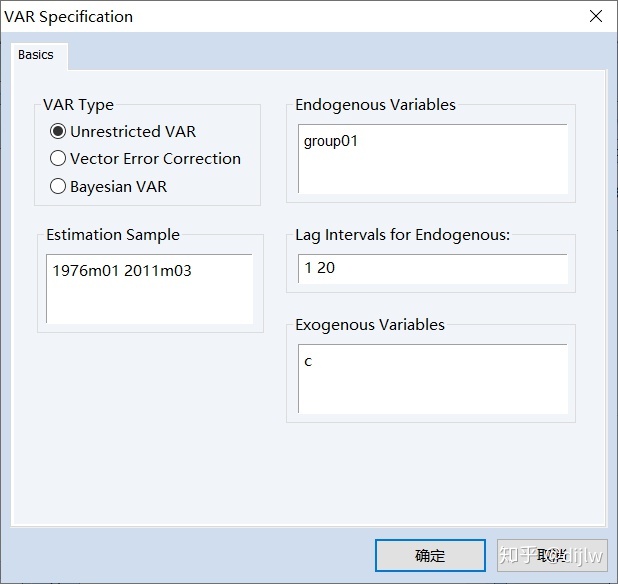
将所有变量划为1组,设定为group01.

在原水平数据上进行VAR建模。滞后阶数设定为20(根据样本数量和变量数量自行设定)。
对刚刚的VAR结构进行最佳阶数确定,其中阶数设定为12
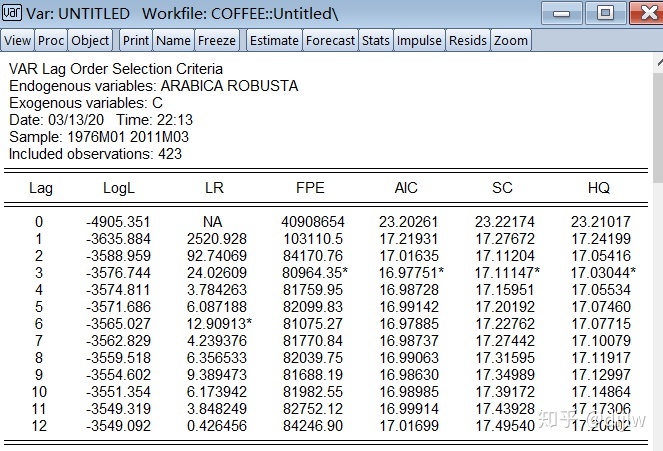
可以看到最佳的阶数在3和6。我们选择3作为暂时的最佳滞后阶数,后续来检验它。
构建VAR使用最佳滞后阶数3。
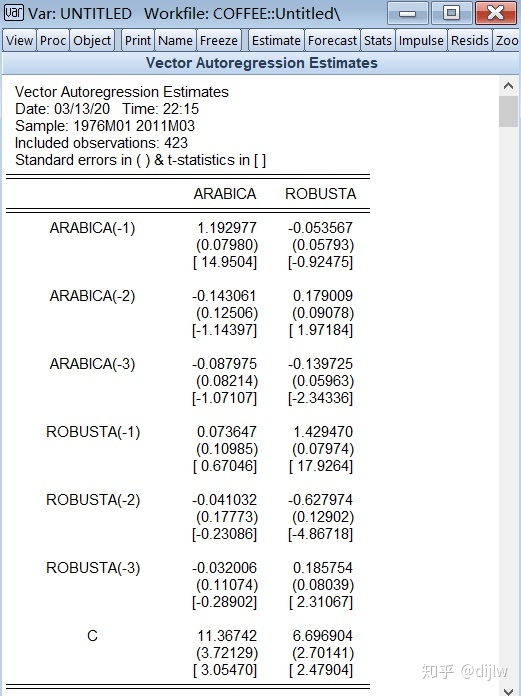
进行模型诊断,主要是残差的自相关检验,我们使用LM 检验。
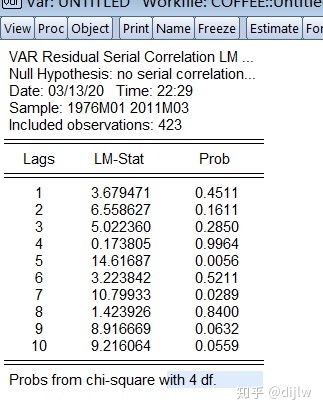
可以看到,在最佳滞后阶数3下,仍然存在自相关(需要所有阶数均不显著才算不存在自相关,可以看到第5阶是显著的)。我们从3开始,增大最佳滞后阶数,并进行VAR建模和模型诊断,发现,在阶数为6时,才不相关。故我们确定最终的最佳滞后阶数为6。
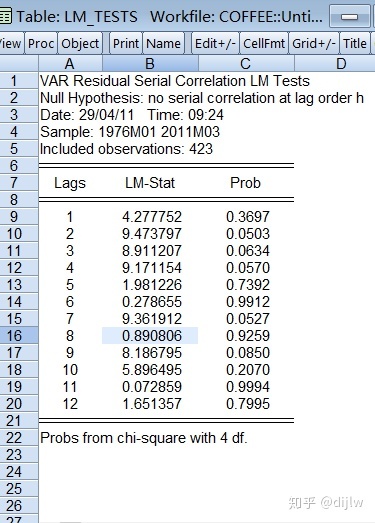
3、重新估计VAR,伴有每个变量的一个额外阶数。
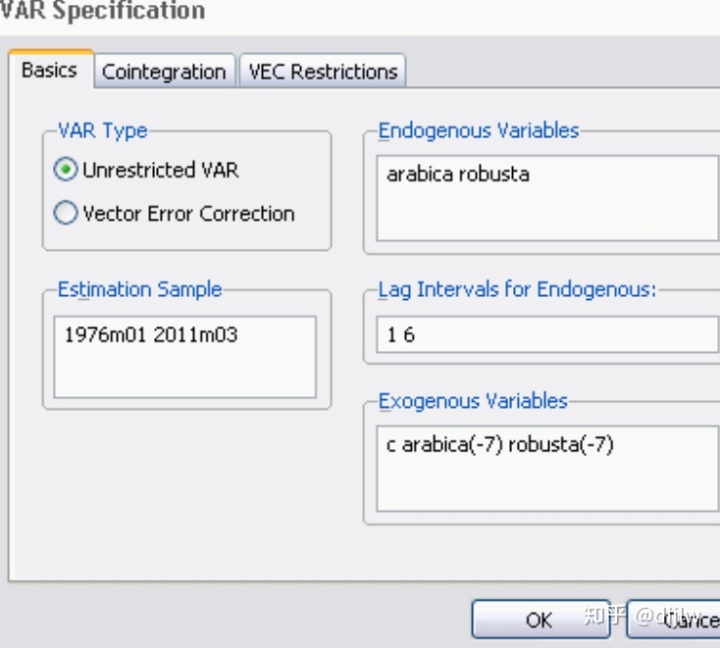
Here is where we need to be careful if we're going to "trick" EViews into doing what we want when we test for causality shortly. Rather than declare the lag interval for the 2 endogenous variables to be from 1 to 7 (the latter being p + m), I'm going to leave the interval at 1 to 6, and declare the extra (7th.) lag of each variable to be an "exogenous" variable. The coefficients of these extra lags will then notbe included when the subsequent Wald tests are conducted. If I just specified the lag interval to be from 1 to 7, then the coefficients of all sevenlags would be included in the Wald tests, and this would be incorrect. If I did that, the the Wald test statistic would not have its usual asymptotic chi-square null distribution.
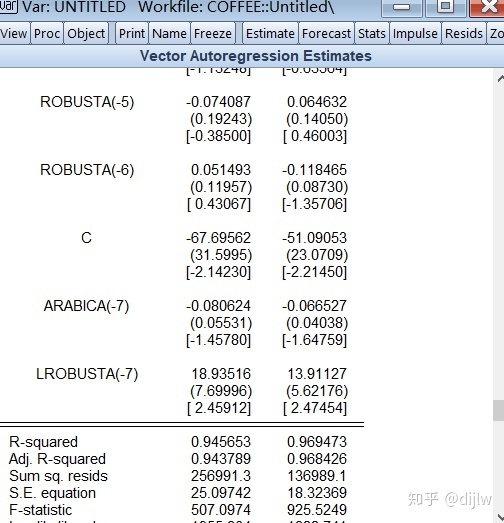
我们确定了最佳滞后阶数6,最大的单位根阶数1,重新构建VAR,所有变量滞后阶数都为7(最佳滞后阶数6+最大的单位根阶数1),区别的是,内生变量是1~6阶数,外生变量是所有变量的第7阶。令VAR(7)为滞后7阶的VAR方程,7阶均内生,令VAR(6)(-7)为滞后7阶的VAR方程,第7阶为外生。那么在EVIEWS估计结果中,VAR(7)和VAR(6)(-7) 并无不同。然而在后续的模型诊断中,即WALD检验中,区别就体现了,VAR(6)(-7)得到的granger检验是有效的。
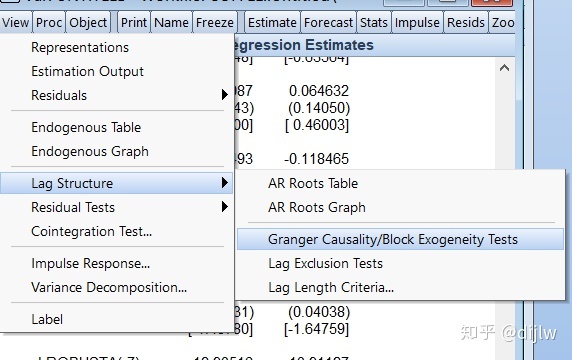
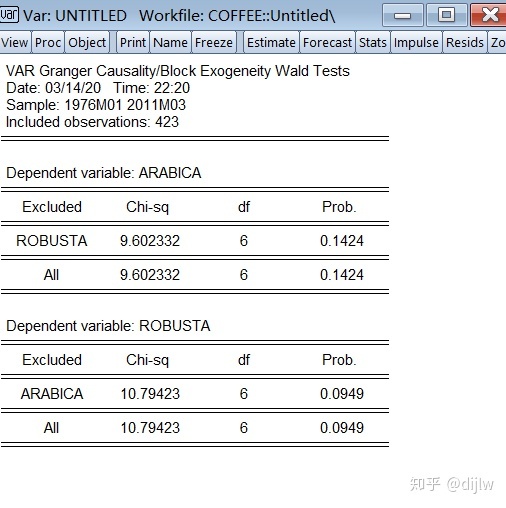
需要注意的一些事项:
在测试Granger非因果关系时,不要使用差分数据去构建VAR。
如果将VAR模型 用于其他目的,则如果序列为I(1)而 不是协整的,则使用差分数据构建VAR。
如果出于测试Granger非因果关系的目的将VAR模型用于其他目的,并且发现该系列是协整的,则可以估算VECM模型。
考虑到作为回归函数进入模型的因变量的滞后性,当测试Granger因果关系时,通常的线性约束F检验无效。
不要使用 t-检验来选择VAR模型的最大滞后。如果数据是不平稳,检验统计量甚至不会渐进服从正态分布,并且还存在会影响真实显着性水平的预测试问题。
如果你没有使用TY办法,或某些等效的程序,只是使用普通的Wald检验,你的因果检验的结果将是毫无意义的。
如果所有时间序列都是平稳的,则 m = 0,您将(正确)以“老式”方式测试非因果关系:估算VAR级并将Wald检验应用于相关系数。 维基百科上当前 有关格兰杰因果关系的条目存在很多问题。
三、后续发展
这三篇都是granger test的进一步改进。

值得一提的是,Bauer & Maynard(2012) 提出了surplus-lag 格兰杰因果检验方法,这个方法更为一般,更为好用,它的优点如下,值得全文阅读。
By extending this surplus lag approach to an infinite order VARX framework, we show that it can provide a highly persistence-robust Granger causality test that accommodates i.a stationary, nonstationary, local-to-unity, long-memory, and certain (unmodelled) structural break processes in the forcing variables within the context of a single χ 2null limiting distribution.
它的方法也非常简洁,但是引用的文章很少,网上没有代码。懂得原理可以轻易实现。它把驱动的协变量x整个当作外生变量,并在其加入了额外阶数,WALD检验即可。需要注意的是,我们不可能像在TY方法一样同时检验许多驱动变量,对于每一个驱动变量,我们要重新构造单个的方程,重新找最佳滞后阶数和进行granger检验。

四、参考文献和代码
- Toda Yamamoto,1995 原文
- https://davegiles.blogspot.com/2011/04/testing-for-granger-causality.html 这篇文章是非常使用eviews详细地重现了TY方法,也是本博文的主要参考,本博文使用了这篇文章的数据来展现eviews过程。
- R软件实现的TY代码:
4、此外还有matlab stata中实现的,没有很大必要。
禁止转载,自用,谢谢,欢迎交流。