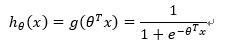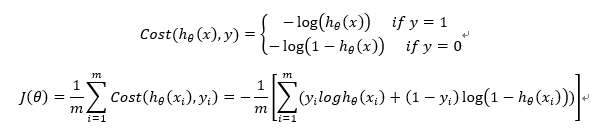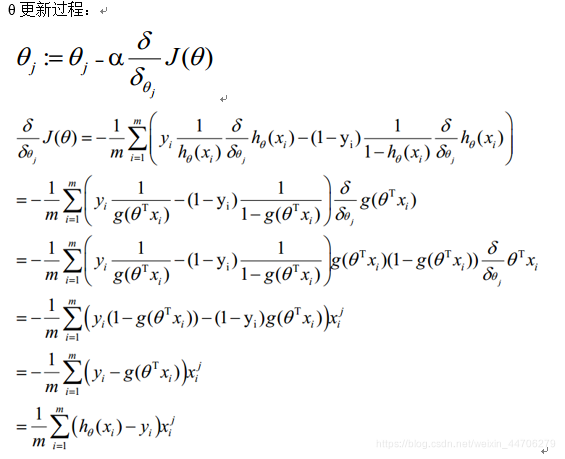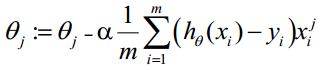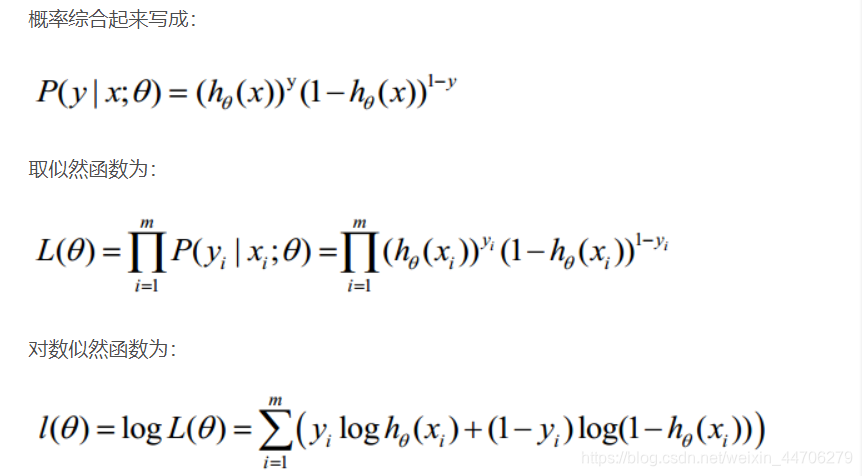初级算法梳理第八期 -Datawhale
【任务2 - 逻辑回归算法梳理】时长:2天
1、逻辑回归与线性回归的联系与区别
2、 逻辑回归的原理
3、逻辑回归损失函数推导及优化
4、 正则化与模型评估指标
5、逻辑回归的优缺点
6、样本不均衡问题解决办法
7、sklearn参数
参考:西瓜书 cs229吴恩达机器学习课程 李航统计学习
谷歌搜索 公式推导参考:http://t.cn/EJ4F9Q0
1.逻辑回归与多重线性回归
logistic回归和线性回归
联系:都是广义线性模型(generalized linear model)
逻辑回归去除Sigmoid映射函数的话就得到一个线性回归。
区别:
线性回归 逻辑回归 目的 预测 分类 函数 拟合函数 预测函数 参数计算方式 最小二乘法 最大似然估计 假设y服从的分布 高斯分布 伯努利分布
2.逻辑回归的原理
定义:逻辑(Logistic Regression)回归是一种用于解决二分类(0 or 1)问题的机器学习算法,用于估计某种事物的可能性。
Exp:如某用户购买某商品的可能性,某病人患有某种疾病的可能性,某广告被用户点击的可能性
建立模型—代价函数—优化—最优模型参数—测试集测试
附:回归常规步骤:
寻找h函数(即预测函数)
构造J函数(损失函数)
想办法使得J函数最小并求得回归参数(θ)
逻辑回归的原理
构造预测函数h:
构造J函数(损失函数):(m个样本,每个样本具有n个特征)
使得J函数最小并求得回归参数(θ)? (使用梯度下降法求最小值)
即:
3.逻辑回归代价函数的推导与优化
4.正则化与模型评估指标
正则化:在训练数据不够多时,或者overtraining时,常常会导致过拟合(over fitting)。正则化即为在此时向原始模型引入额外的信息,以便防止过拟合和提高模型泛化能力性能的一类方法总称。
参数范数惩罚:通过向目标函数中添加一个范数Ω(θ)来降低模型的容量,是一种常用的正则化方法。将正则化后的损失函数极为J_(θ;X,y)=J(θ;X,y) + α ·Ω(θ),α权衡范数惩罚项相对贡献
L2正则化:向目标函数中添加一个正则化项Ω(θ)=1/2· |w|^2,是权重更加接近原点。
L1正则化:向目标函数中添加一个正则化项Ω(θ)=Σ|wi|,即各项参数的绝对值之和。
模型评估指标:
分类问题:1、混淆矩阵2、准确率(Accuracy)3、精确率(Precision)
4、召回率(Recall)5、F1 score 6、ROC曲线 7、AUC 8、PR曲线
回归问题:1. 平均绝对误差(MAE)2. 平均平方误差(MSE)3、均方根误差(RMSE)
4、解释变异 5、决定系数
5.逻辑回归的优缺点
优点:(模型)1.模型清晰,背后概率的推导经得住推敲
(输出)2.输出值落在0-1之间,并具有概率意义
(参数)3.参数代表每个特征输出的影响,可解释性强
(简单高效可扩展)4.实现简单非常高效,可使用online learning方式轻松更新参数缺点:(特征相关状况)1.本质是线性的分类器,处理不好特征之间的相关情况。
(特征空间)2.特征空间很大时,性能不好
(精度)3.容易欠拟合,精度不高
6.样本不均衡性问题解决办法
数据样本不均衡:
很多算法都基于数据分布是均匀的假设
实际数据分布很不均衡,都会存在“长尾效应”
样本不均衡问题如何解决:
基本思路是让正负样本在训练过程中拥有相同话语权
1.采样:通过对训练集进行处理使不平衡的数据集变成平衡的数据集,大部分会对最终结果带来提升。
上采样(over sampling):把样本较少那类复制多份
下采样(under sampling):把样本较多那类剔除一些样本(选部分样本)
2.数据合成:利用已有的样本生成更多样本
3.加权:对不同类别分错的代价不同
4.一分类问题:对于正负样本极不均衡的场景,看作一分类(one class Learning)或异常检测(Novelty Detection)问题