数组
从本质上讲,数组与顺序表、链表、栈和队列一样,都用来存储具有 “一对一” 逻辑关系数据的线性存储结构。只因各编程语言都默认将数组作为基本数据类型,使初学者对数组有了 “只是基本数据类型,不是存储结构” 的误解。
不仅如此,数组和其他线性存储结构不同,顺序表、链表、栈和队列存储的都是不可再分的数据元素(如数字 5、字符 ‘a’ 等),而数组既可以用来存储不可再分的数据元素,也可以用来存储像顺序表、链表这样的数据结构。
public class Demo01 {
public static void main(String[] args) {
/**
* 1、数组的概念:用来存储一组相同数据类型的数
* 2、Java中数组的定义
* 数据类型[] 数组名
* 3、初始化:数据类型[] 数组名 = new int[6];
* 数据类型[] 数组名 = {1,2,3,4,5};
* 4、数组在内存中分配的是连续的空间
*/
String[] fruits = {"apple", "pear", "watermelon", "banana", "Pineapple"};
/* for (int i = 0; i < fruits.length; i++) {
System.out.println(fruits[i]);
}*/
/* Arrays.stream(fruits).forEach(item -> System.out.print(item));
int[] nums = new int[1000];
Random random = new Random();
for (int i = 0; i < 1000; i++) {
nums[i] = random.nextInt(100000);
}
Arrays.stream(nums).map(item -> item + 10).filter(item -> item % 2 > 0).forEach(System.out::println);
*/
// 1、对每个数据+10
// 2、过滤奇数
// Integer.parseInt("".substring(-4));
String str = "ababccddeesss";// 字符串中只包含小写子母
// 统计每个字符出现的次数
int[] counts = new int[26];
for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
counts[c - 'a']++;
}
for (int item : counts) {
System.out.println(item);
}
Map<Character, Integer> map = new HashMap<>();
/* for (int i = 0; i < str.length(); i++) {
char c = str.charAt(i);
if (!map.containsKey(c)) {
map.put(c, 1);
} else {
map.put(c, map.get(c) + 1);
}
}*/
}
}
1、数组基础
<1> 用来存储一组类型相同的数据
<2> 在内存中,分配连续的空间,数组创建时要指定容量(大小)
<3> 数据类型[] 数组名 int[] arr = new int[10] int[] arr2 = {1,2,3,4}
<4>索引—访问数组时通过索引进行操作
<5> 索引从0开始,最大为 arr.length -1
<6> 常见的错误: NullPointException ArrayIndexOutOfBoundsException
<7> 常见的数组: 字符串, 对象数组,哈希表
2、索引
使用数组时,最重要的就是数组的索引,通过索引可以对数组进行改和查操作。
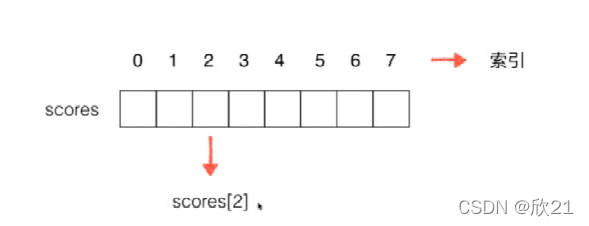
索引:可以有语义,也可以没有语义(理解)。
数组最大的优点:快速查询。
数组最好应用于索引有语义的情况。
并非所有有语义的数字都可以作为数组的索引,例如:610521199610111188
数组也是可以处理“索引没有语义”的情况。
产生的问题
索引没有语意,如何表示没有元素?
如何添加元素?如何删除元素?
3、可变数组
基于Java中的数组,进行二次封装,制作属于我们自己的数组(可变数组)。
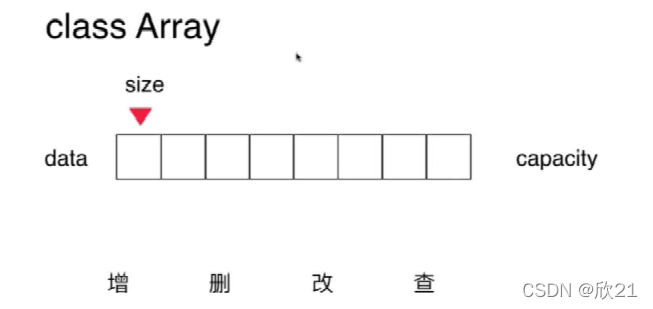
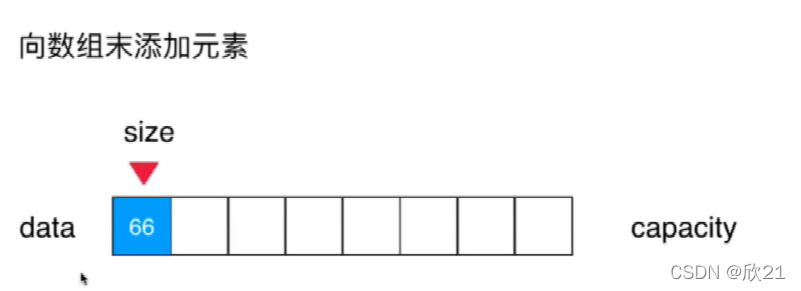
4、向数组中添加元素
5、向指定位置添加元素
向指定位置添加元素
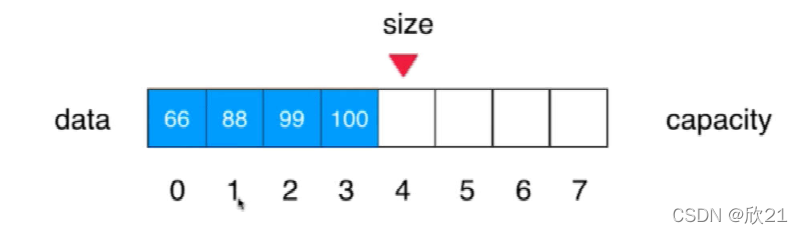
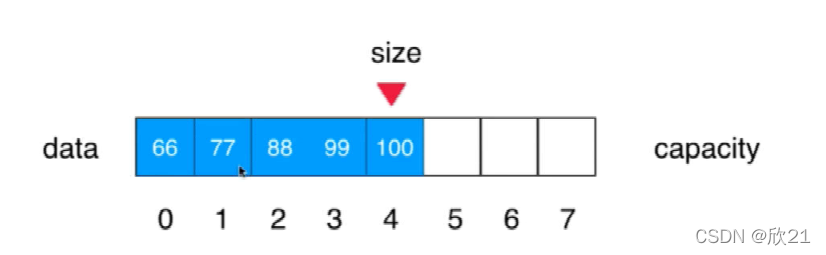
把77插入到索引为1的位置
6、向数组头添加元素
7、获取指定位置的元素和修改指定位置的元素
8、包含、搜索和删除元素
删除指定位置元素
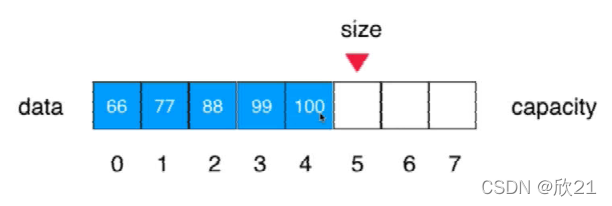
删除索引为1的元素
针对上面的逻辑,我们可以删除指定的元素 public void removeElement(int e);
注意:我们的数组中可能存在重复的元素,此方法只删除第一次找到的元素。
9、使用泛型(“任意”类型的数组)
不可以是基本数据类型,只能是类对象 。
基本数据类型: 8种
byte char boolean int short float double long
每种基本数据类型都有一个对应的包装类。
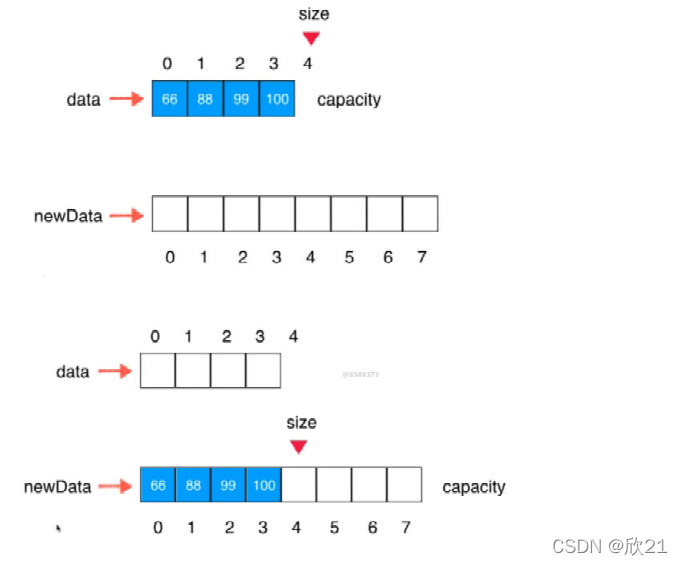
10、动态数组
11、简单的时间复杂度分析
在算法领域,使用复杂度分析的内容来评价你写的代码性能如何。
leetCode、牛客网上的题目不只要求做出来,还要求在指定的时间内完成。
通常情况下我们只需要简单的时间复杂度分析就足够了。
O(1), O(n) , O(Ign) ,O(nlogn) ,O(n^2)
大O描述的是算法的运行时间和输入数据之间的关系
public static int sum(int [] nums){
int sum = 0;
for(int num: nums) sum += num;
return sum;
}
O(n):n是nums中的元素个数,算法和n呈线性关系
为什么要用大0,叫做O(n)?
忽略常数。 实际时间T=c1*n+ c2
T=2n+ 2 O(n)
T = 2000n + 10000 O(n)
T=1nn+0 O(n^2)
渐进时间复杂度,描述n趋近于无穷的情况
12、分析动态数组的时间复杂度
添加操作 O(n)
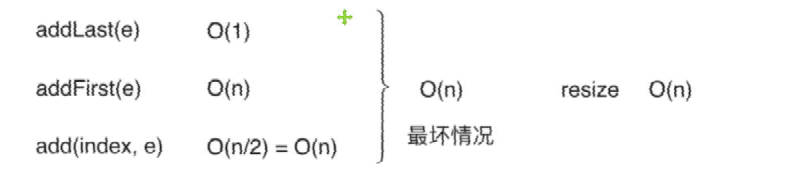
删除操作 O(n)
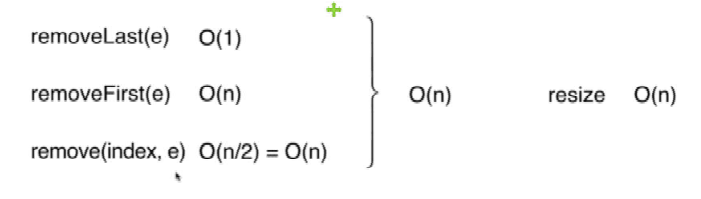
修改操作
set(index,e) O(1)
查找操作
get(index) O(1)
contains(e) O(n)
find(e) O(n)
综合
增 O(n)
删 O(n)
改 已知索引O(1);未知索引O(n)
查 已知索引O(1);未知索引O(n)
13、resize的复杂度分析(均摊复杂度)
resize O(n)
9次addLast操作,触发resize, 总共进行了17次基本操作
平均,每次addLast操作,进行2次基本操作
假设capacity = n,n+1次addLast,触发resize,总共进行2n+1次基本操作
平均,每次addLast操作, 进行2次基本操作
这样均摊计算:时间复杂度为O(1)
14、复杂度的震荡
当我们同时进行addLast和removeLast的操作
出现问题的原因:removeLast 时 resize 过于着急 (Eager)
解决方案:Lazy