神经网络中的各种优化方法

神经网络中的优化方法

在上一章，我们已经讲了参数的初始化，下一步就是通过训练数据集，来寻找使得损失函数值最小的（W,b），在这个过程中，一个好的优化算法往往可以帮助我们更加快速、准确地找到合适的参数。因此，本文就神经网络中的各种优化算法做简要的分析与讨论

长期以来，人们普遍认为，神经网络优化问题困难是因为较大的神经网络中包含很多局部极小值，使得算法容易陷入到其中某些点。后来，人们才发现，在深度学习的寻优过程中，鞍点所造成的困难，远比局部最小值大的多。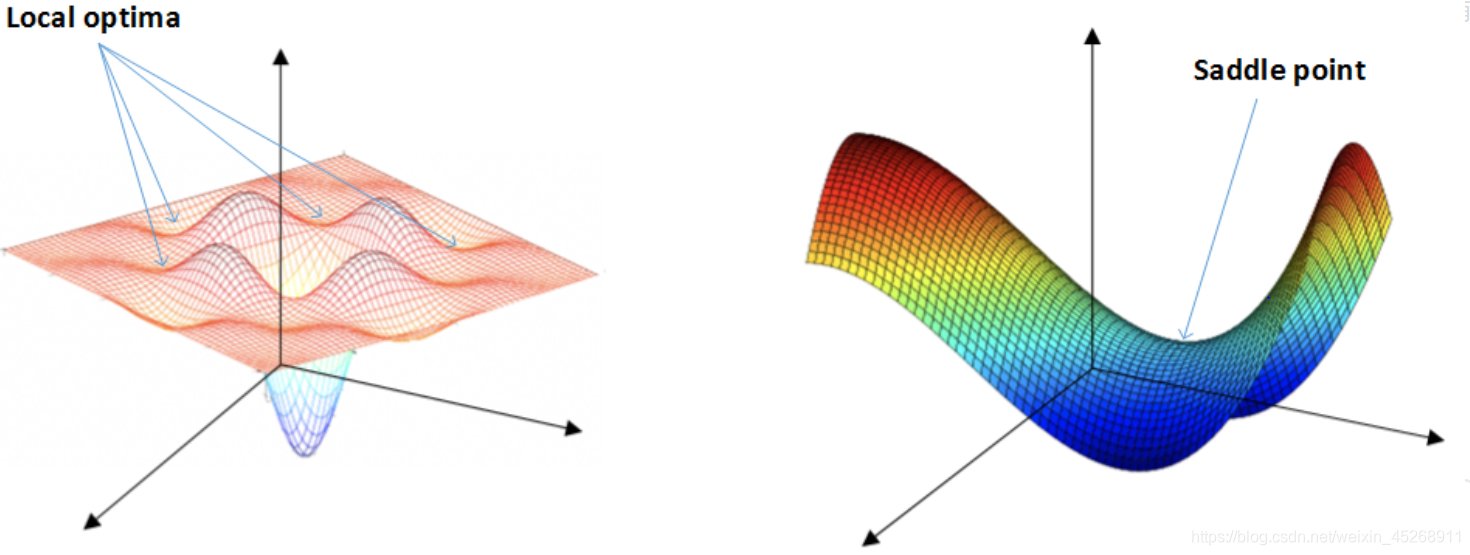

如上图左所示，神经网络只有两个参数时的情况（水平方向分别为两个参数，纵轴代表损失函数），有多个局部最小值，但大多数神经网络具有高维参数，如上图右所示，可看到有鞍点。
鞍点和局部极小值相同的是，在该点处的梯度都等于零，不同在于在鞍点附近Hessian矩阵是不定的(行列式小于0)，而在局部极值附近的Hessian矩阵是正定的。
鞍点处的梯度为零，鞍点通常被相同误差值的平面所包围（这个平面又叫Plateaus，Plateaus是梯度接近于零的平缓区域，会降低神经网络学习速度），在高维的情形，这个鞍点附近的平坦区域范围可能非常大，这使得SGD算法很难脱离区域，即可能会长时间卡在该点附近（因为梯度在所有维度上接近于零）。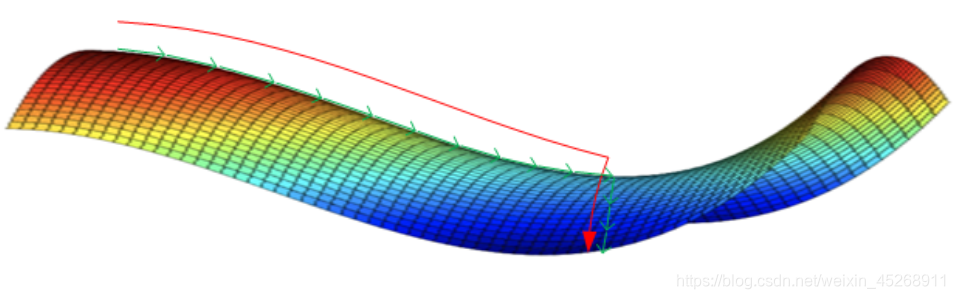

下面我们就来具体地分析一些优化算法，来看它们是如何解决这个问题的。

一、Gradient Descent梯度下降

梯度下降算法工作的方式就是重复计算梯度∇C，然后沿着相反的方向移动，其对于（W,b）的更新公式如下

批量梯度下降每次学习都使用整个训练集，因此其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长。

二、Mini-Batch Gradient descent

当我们的样本数量巨大的时候，如果我们还是使用之前的梯度下降的话，就会使我们的训练效率下降，因此，我们引入了Mini-Batch，Mini-Batch就是把数据分为numbers/min−batch个组，其中numbers代表样本总数目，每组里有min−batch个样本，然后按批次的计算梯度和loss，而不是所有样本处理完再计算，这样会加快训练速度.
这里的前提条件是：我们默认为小样本所得到的梯度均值是和数据集的样本数据梯度均值是差不多。如下：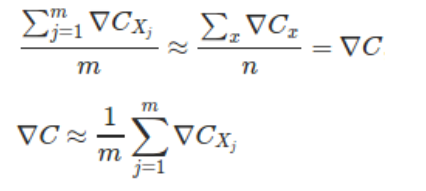

这时我们可以得到（W,b）的更新策略如下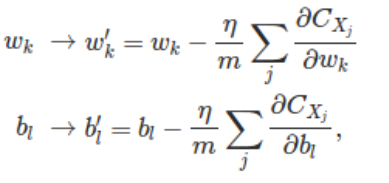

使用mini-batch之后，我们的代价曲线就可以不是单调递减的了，它包含了很多噪声，是一种曲曲折折的样子，但是总体的趋势是下降的，cost曲线这么曲折是因为也许我们取的第一个样本比较好算，可是另一个样本，也许出于偶然，变得比较难算，那么相应的代价也会上升。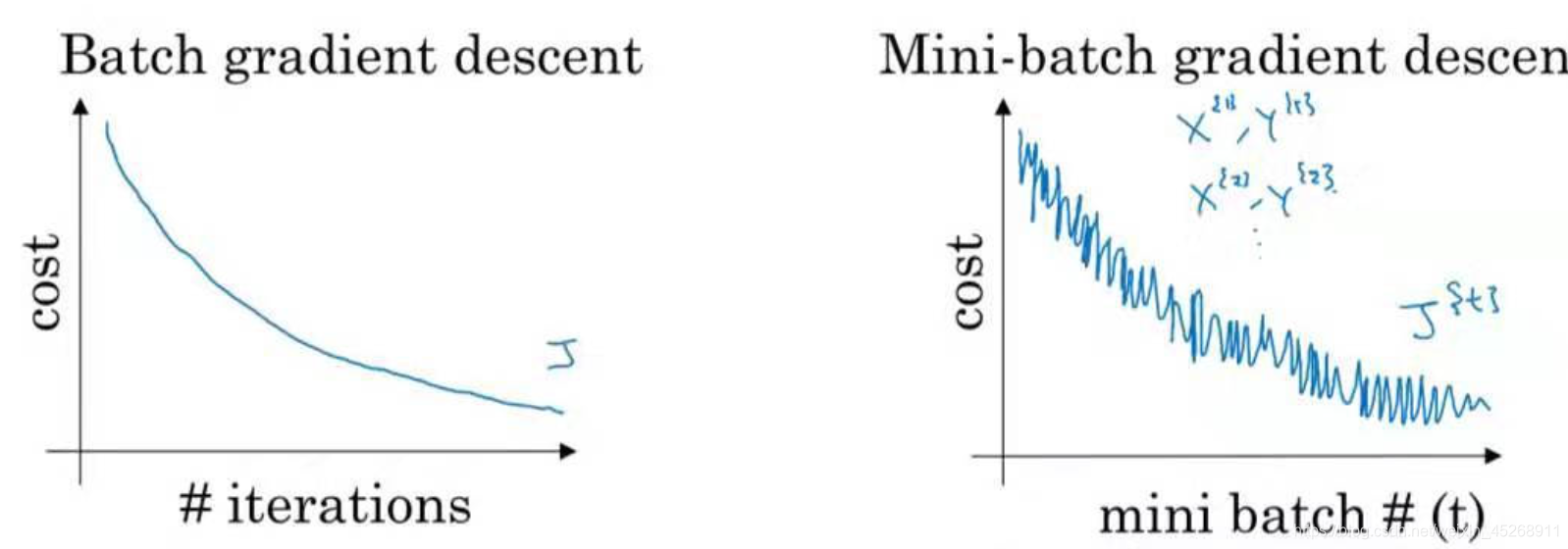

三、SGD随机梯度下降

随机梯度下降就是 min-batch size = 1，每次更新都只用一对样本，计算量小，更新频率高，但容易导致模型不稳定。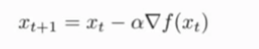

while True:
   dx = compute_gradient(x)
   x += learning_rate * dx

随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，优化的轨迹会如图所示，因为很多函数的梯度方向并不是直接朝向最小值的，所以沿着梯度前进的时候可能会来回反复。这个问题在高维空间中更加普遍。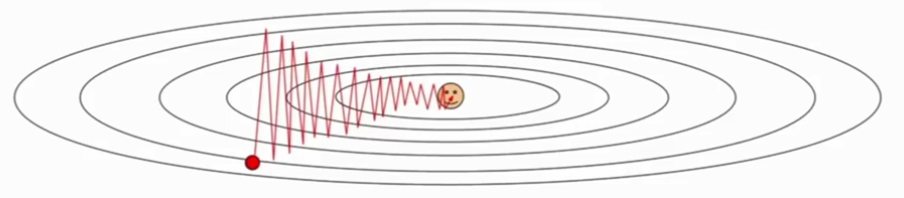

总的来说，梯度下降算法虽效果较好，但它存在以下问题

1. 选择一个合理的学习速率很难。如果学习速率过小，则会导致收敛速度很慢。如果学习速率过大，那么其会阻碍收敛，即在极值点附近会振荡
2. 对于非凸目标函数，容易陷入那些次优的局部极值点中，在神经网络中，最严重的是无法逃离鞍点。

四、SGD+Momentum

动量方法主要是为了解决Hessian矩阵病态条件问题提出的，如图所示，红色为SGD+Momentum。黑色为SGD。可以看到黑色为典型Hessian矩阵病态的情况，相当于大幅度的徘徊着向最低点前进。
而由于动量积攒了历史的梯度，如点P前一刻的梯度与当前的梯度方向几乎相反。因此原本在P点原本要大幅徘徊的梯度，主要受到前一时刻的影响，而导致在当前时刻的梯度幅度减小。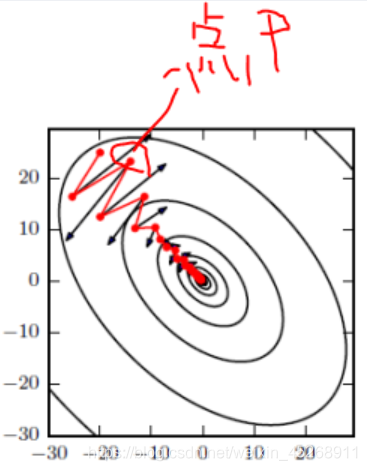

直观上讲就是，加上动量项就像从山顶滚下一个球，求往下滚的时候累积了前面的动量(动量不断增加)，因此速度变得越来越快，直到到达终点。在更新模型参数时，对于那些当前的梯度方向与上一次梯度方向相同的参数，那么进行加强，即这些方向上更快了；对于那些当前的梯度方向与上一次梯度方向不同的参数，那么进行削减，即这些方向上减慢了。因此可以获得更快的收敛速度与减少振荡。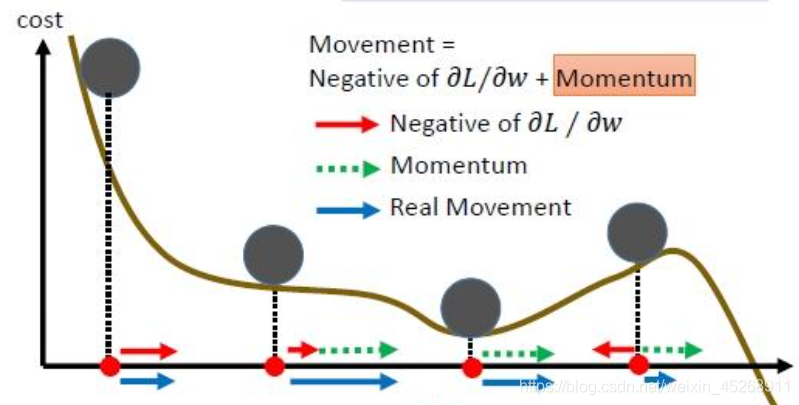
其计算公式为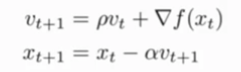

vx = 0
while True:
   dx = compute_gradient(x)
   vx = rho * vx + dx
   x += learning_rate * vx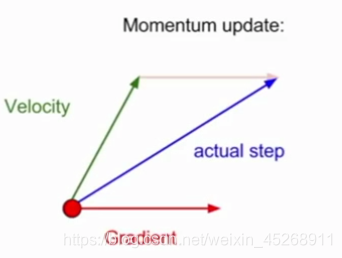

五、Nesterov Momentum

Nesterov 相当于添加了矫正因子的Momentum。与Momentum唯一区别就是，计算梯度的不同，Nesterov先用当前的速度v更新一遍参数，在用更新的临时参数计算梯度。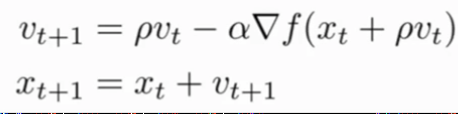

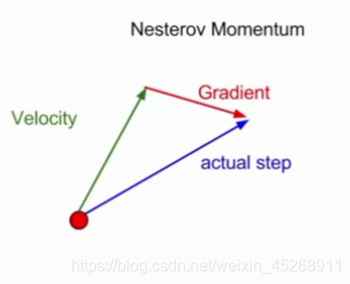
如上图所示，既然我们知道动量将会把我们带到绿色箭头指向的点，我们就不要在原点（红色点）那里计算梯度了。使用Nesterov动量，我们就在这个“向前看”的地方计算梯度。举个通俗的例子就是，你在下坡时，如果在下坡快到底，但又未到底时，动量梯度下降会让你冲到坡的对面去。Nesterov梯度下降会预知你的下一步将会时到坡的对面去，所以会提示你提前刹车，避免过度冲到坡的对面去。
在实际编程时，我们习惯于和SGD+Momentum一样的表示方法，所以公式可变换为下面这样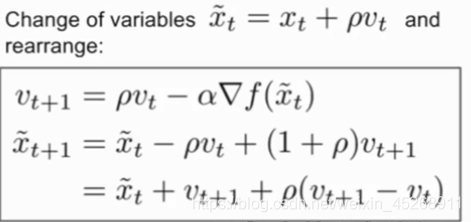

dx = compute_gradient(x)
old_v = v
v = rho * v - learning_rate * dx
x += -rho*old_v +(1+rho) * v

六、Adagrad

AdaGrad的核心思想是，在优化的过程中，需要保持一个在训练过程中每一步的梯度的平方和的持续估计，与速度项不同的是，现在我们有了一个梯度的平方项，在训练时，我们会一直累加当前梯度的平方到这个梯度平方项，当我们在更新我们的参数向量时，我们会除以这个梯度平方项。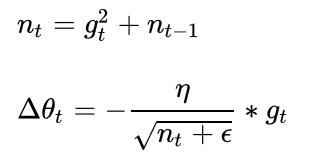

grad_squared = 0
while True:
   dx = compute_gradient(x)
   grad_squared += dx*dx
   x -= learning_rate * dx /(np.sqrt(grad_squared) + 1e-7)

如果我们有两个坐标轴，在一个轴上梯度很大，在另一个轴上梯度很小，通过我们不断地累加这个小梯度，会加速在小梯度维度上的学习速度；在另一个梯度很大的轴上，我们会除以一个非常大的数，所以我们会降低这个维度方向上的训练速度；
需要说明的是，使用AdaGrad时，随着时间的增加，步长会越来越小，因为我们一直在随时间更新梯度平方的估计值，这个估计值一直随时间单调递增，导致我们的步长随时间越来越小。

七、RMSprop

RMSprop优化器的原理类似于动量梯度下降算法。RMSprop优化器限制了垂直方向上的振荡，使我们的算法可以在水平方向上采取更大的步，进行更快地收敛。

对于上面的这个椭圆形的抛物面（图中的椭圆代表等高线），沿着横轴收敛速度是最快的，所以我们希望在横轴（假设记为w1）方向步长大一些，在纵轴（假设记为w2）方向步长小一些。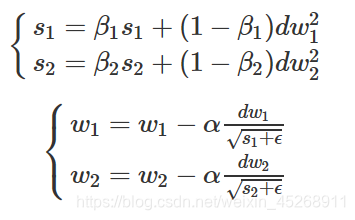

s是对梯度的平方做了一次平滑。在更新w时，先用梯度除以根号下s1+ϵ，相当于对梯度做了一次归一化。如果某个方向上梯度震荡很大，应该减小其步长；而震荡大，则这个方向的s也较大，除完之后，归一化的梯度就小了；如果某个方向上梯度震荡很小，应该增大其步长；而震荡小，则这个方向的s也较小，归一化的梯度就大了。因此，通过RMSprop，我们可以调整不同维度上的步长，加快收敛速度。把上式合并后，RMSprop迭代更新公式如下：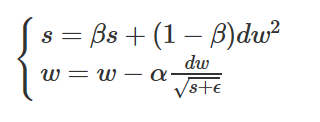

grad_squared = 0
while True:
   dx = compute_gradient(x)
   grad_squared = decay_rate * grad_squared + (1 - decay_rate) *dx *dx
   x -= learning_rate * dx / (np.sqrt(grad_squared) + 1e-7)

八、Adam

Adam 是结合了 Momentum 和 RMSProp 的算法。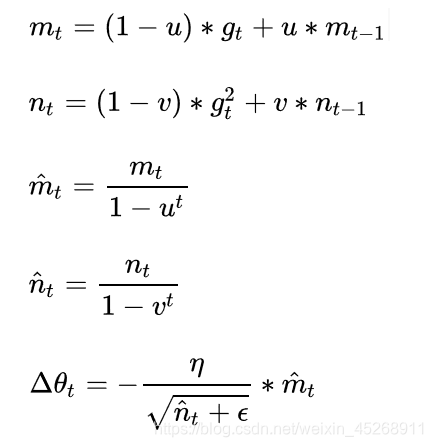

first_moment = 0
second_moment = 0
for t in range(num_iterations):
   dx = compute_gradient(x)
   first_moment = beta1 * first_moment +(1-beta1) * dx
   second_moment = beta2 * second_moment + (1-beta2) * dx * dx
   first_unbias = first_moment / (1 - beta1**t)
   second_unbias = second_moment / (1-beta2**t)
   x -= learning_rate * first_unbias / (np.sqrt(second_unbias) + 1e-7)

Adam算法表现非常好，基本能够解决任何问题，beta1=0.9，beta2=0.999，learning_rate=1e-3 or 5e-4，这样的参数设定对于任何结构的都比较好