阅读了一些博客和论文,发现内容很多,比较繁杂。本文力图用最简洁的话语从另一个角度概括Xgboost,主要参考内容见:
1.原文:https://arxiv.org/pdf/1603.02754v1.pdf
2.陈天奇 PPT:https://pan.baidu.com/s/10NWfRM9qimswGxPsF9VlDw 密码:v3y6
3.介绍详细的blog:https://blog.csdn.net/v_JULY_v/article/details/81410574
Xgboost是一个很有名梯度提升树方法,由陈天奇老师于2016年提出,是在梯度提升决策树(GBDT)的基础上改进得到。其主要区别在于xgboost的目标函数泰勒展开时保留了二阶项。xgboost的核心思想在于:不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。
1 回首决策树
其实可以看到上述问题的关键在于如何根据残差构建每一个决策树,使得整体效果达到最好。在此之前我们先回首一下决策树的构建过程。所谓决策树就是在各个节点上利用一些指标(衡量划分的准确性,类似loss),递归地构建树。比如对于未划分的样本,可以视为都处于根节点。基于某一个特征,可以对样本划分,可以根据上述的指标遍历搜索何种划分使得模型达到最后,这样就划分出了一个简单的二叉树。接着递归划分就可以构造出整个树。
在决策树的构建过程中,一般使用基于信息论中的熵的一些指标,包括基尼系数,信息增益等。这里以信息增益做简要介绍。首先熵的定义如下:H ( X ) = − ∑ i = 1 n p i log p i H(X)=-\sum_{i=1}^{n}p_{i}\log p_{i}H(X)=−i=1∑npilogpi其中X是一个离散随机变量,p i p_{i}pi可以看作是第i个取值的概率。这个要怎么理解呢?可以类比物理中的定义,熵越大,随机变量的不确定性越大。然后举个例子验证一下,随机变量是确定的,即一个取值的概率为1,则熵为0.
此外另一个概念是条件熵,其定义为X给定条件下,Y的条件概率分布的熵对X的数学期望,即:H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y|X)=\sum_{i=1}^{n}p_{i}H(Y|X=x_{i})H(Y∣X)=i=1∑npiH(Y∣X=xi)条件熵表示已知随机变量X的条件下随机变量Y的不确定性。
进而我们可以定义出信息增益,即在已知A划分之后随机变量Y的不确定性的变化。即为:g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D,A)=H(D)-H(D|A)g(D,A)=H(D)−H(D∣A)其中D可以看为是根节点上的所有样本,A是一个特征。一般地,上H(Y)与条件上H(Y|X)之差成为互信息,决策数学习中地信息增益可以看作训练数据集中类与特征地互信息。
通过决策树地构建过程,我们可以发现构建树地关键在于根据信息增益选取特征。而XGBOOST作为树地一个集成,是如何构建树地呢?
2 Xgboost 树地构建
Xgboost 通过boost的方法集成了很多树,不同于随机森林所使用的bagging的方法。boost的方法强调树与树之间的关联性。比较著名的算法还有Adaboost,GBDT。本文要介绍的Xgboost 通过Additive training的方式进行树的构建,简单说就是:不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数,去拟合上次预测的残差。
公式表示如下:

其中y ^ i ( t ) \hat{y}_{i}^{(t)}y^i(t)视为前t棵树对第i个样本的输出,f t ( x i ) f_{t}(x_{i})ft(xi)是第t棵树的输出。所以我们只需关注这个f t ( x i ) f_{t}(x_{i})ft(xi)是怎么构建的,进而就可以累计构建出整个“森林”。
2.1 f t f_{t}ft通过求解一个优化问题构建

其中y i y_{i}yi是真实标签,y ^ i ( t − 1 ) \hat{y}_{i}^{(t-1)}y^i(t−1)视为之前构建的“森林”预测的结果,Ω ( f t ) \Omega(f_{t})Ω(ft)是用来衡量第t棵树f t f_{t}ft的复杂度,理解为正则项。Ω ( f t ) \Omega(f_{t})Ω(ft)前面的求和项是多个样本加上要构建的第t树后得到的模型总的预测结果loss求和。这里的loss函数可以是多种loss。
2.2 优化问题求解
那么上式如何优化呢?显然这种树的结构不可以常规的优化算法求解。但基本的逻辑类似,总得来说是先通过泰勒展开化简,再通过求导计算极值。但是因为树的结构比较特殊,变量不是一个向量,所以要进行一个变形。这里就要回到决策树构建的思路上。下面细细讲解:
2.2.1 泰勒展开

这里都是标准化的东西,没有非常tricky的操作。
2.2.2 树的复杂度
树的复杂度定义如下: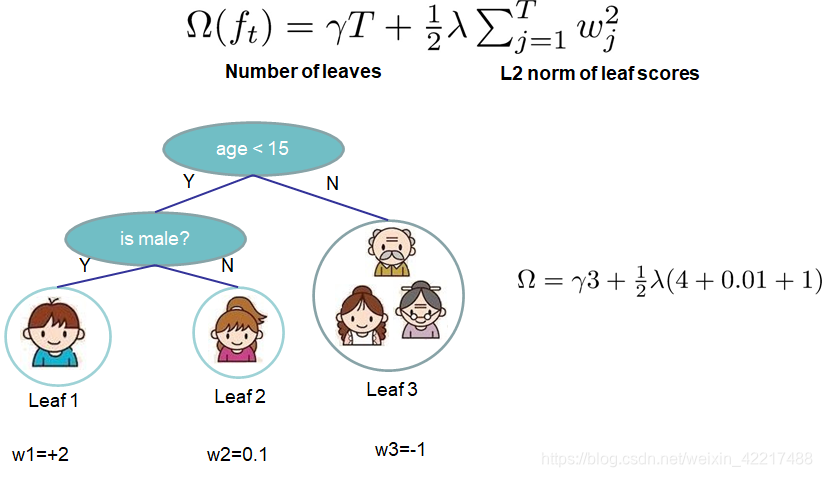
其中j是不同叶节点的标号,T是叶节点的个数,ω j \omega_{j}ωj是这个叶节点上的值,γ \gammaγ是一个调节复杂度的常数。这里需要的注意的是,每个叶节点中的样本的个数可能不是1个。
2.2.3 Object function的进一步化简及求解

这里I j I_{j}Ij定义了第j个叶节点中的样本的标号。

整个求解过程如上,我们求解得到了当树的结构固定的时候(即q(x)固定),最优的节点的值,以及最小的Obj。所以现在主要的问题是确定树的结构了。
这时就要回到第一节中决策树的构建方法中去,我们要通过第一节的那种方式来最小化这个Obj。实践中常采用贪心算法如下:
类比第一节,这也是一种递归算法,不同之处在于选择特征的指标发生了变化。
树的构建与剪枝。
总结,对于Xgboost也是一种tree-based方法,所以在学习过程中一定要紧扣树的构建。类比普通的决策树方法,或许会更容易理解。