一个连通图的生成树是一个极小的连通子图，它含有图中全部的顶点，但只有足以构成一棵树（不存在回路）的n-1条边。将生成树的各边的权值相加，就是代价，我们将连通网的最小代价生成树称为最小生成树。

查找无向连通网的最小生成树，有两种经典算法—普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法，本文介绍普里姆算法。

理解本文需要先了解图的一些构造方法，参考【数据结构】图的创建与遍历

一、定义

普利姆算法定义如下：

假设$N=(V,E)$是连通网，$TE$是$N$上最小生成树中边的集合。算法从$U=\{u_0\}(u_0\in V),TE=\{\}$开始。重复执行以下操作：在所有$u\in U,v\in V-U$的边$(u,v)\in E$中找到一条代价最小的边$(u_0,v_0)$并入集合$TE$，同时$v_0$并入$U$，直至$U=V$为止。此时$TE$中必有$n-1$条边，则$T=(V,TE)$为$N$的最小生成树。

二、实现思路

下图是一个连通网，我们以此来介绍普利姆算法的实现过程。

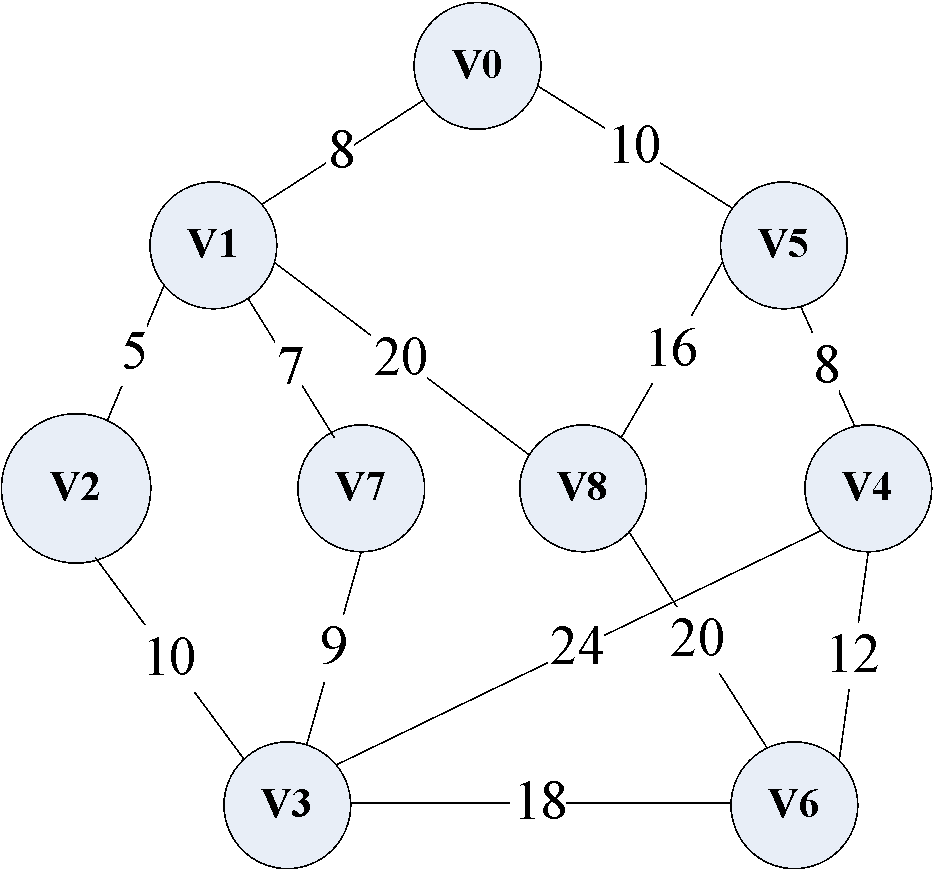
此连通网$N=(V,E)$，V是所有顶点的集合，E是所有边的集合。

$U=\{v_0\}(v_0\in V)$，$U$是生成树的点集合，以$v_0$为起点，开始寻找最短路径。

$TE=\{\}$是生成树的边集合，初始为空。

每次寻找离生成树最近的顶点，将其纳入生成树中，直至包含所有顶点：

（1）

$U=\{v_0,v_1\}$，$TE=\{(v_0,v_1)\}$。

（2）

$U=\{v_0,v_1,v_2\}$，$TE=\{(v_0,v_1),(v_1,v_2)\}$。

（3）

$U=\{v_0,v_1,v_2,v_7\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7)\}$。

（4）

$U=\{v_0,v_1,v_2,v_7,v_3\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7),(v_7,v_3)\}$。

（5）

$U=\{v_0,v_1,v_2,v_7,v_3,v_5\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7),(v_7,v_3),(v_0,v_5)\}$。

（6）

$U=\{v_0,v_1,v_2,v_7,v_3,v_5,v_4\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7),(v_7,v_3),(v_0,v_5),(v_5,v_4)\}$。

（7）

$U=\{v_0,v_1,v_2,v_7,v_3,v_5,v_4,v_6\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7),(v_7,v_3),(v_0,v_5),(v_5,v_4),(v_4,v_6)\}$。

（8）

$U=\{v_0,v_1,v_2,v_7,v_3,v_5,v_4,v_6,v_8\}$，$TE=\{(v_0,v_1),(v_1,v_2),(v_1,v_7),(v_7,v_3),(v_0,v_5),(v_5,v_4),(v_4,v_6),(v_5,v_8)\}$。

三、实现程序

程序解析：

（1）我们知道树中除了根结点没有父结点以外，其他的结点均有且只有一个父结点，那么结点与其父结点之间的边也只有一条。

（2）定义adjvex数组，其下标表示0-n的全部结点，adjvex[i]的值表示生成树中结点i的父结点下标。

（3）定义lowcost数组，其下标表示0-n的全部结点，lowcost[i]的值表示结点i与当前生成树的最短直接距离（若结点i已经在生成树中，则对应的值为0，若结点i与生成树没有边直接相连，则对应的值为$\infty$）。

（4）11行：当前生成树只有$v_0$，临接矩阵arc的第0行赋给lowcost。

（5）12行：以$v_0$为根结点开始建立生成树，因为根结点没有父结点，因此adjvex数组初始化都为v_0的下标，表示其他结点还未加入生成树。

（6）22-33行：寻找离当前生成树的距离最短的结点，并打印此结点与生成树之间的最短边，lowcost[k] = 0将此结点加入到生成树中。

（7）35-41行：更新lowcost数组，因为生成树新添加了一个结点k，重新计算各结点与生成树的距离。并更新adjvex数组，将结点k添加在可能的子结点的位置中。

生成树添加结点1后，lowcost的更新：

生成树中结点1可能的子结点有结点2、7、8：

（8）重复步骤（6）、（7），生成树每次添加一个结点，重复n-1次，生成树包含网的所有顶点，即为最小生成树。

void MinSpanTree_Prim(MGraph G)
{
    int min, i, j, k;
    int adjvex[MAXVEX]; //生成树中子结点与其父结点的对应关系，MAXVEX为最大的顶点数量
    int lowcost[MAXVEX]; //图中各顶点与生成树的最短直接距离
    lowcost[0] = 0; //V0加入生成树
    adjvex[0] = 0; //第一个顶点下标为0

    for (i = 1; i < G.numVertexes; i++)
    {
        lowcost[i] = G.arc[0][i]; //将V0顶点与之有边的权值存入数组
        adjvex[i] = 0; //初始化都为V0的下标
    }

    for (i = 1; i < G.numVertexes; i++) //向生成树中添加G.numVertexes-1次顶点
    {
        min = INFINITY; //初始化最小权值为无穷大

        j = 1;
        k = 0;

        while(j < G.numVertexes) //循环全部顶点
        {
            if (lowcost[j] != 0 && lowcost[j] < min) //权值不为0且权值小于min
            {
                min = lowcost[j]; //则让当前权值成为最小值
                k = j; //将当前最小值的下标存入k
            }
            j++;
        }

        printf(" (%d, %d) ", adjvex[k], k); //打印当前顶点边中权值最小边
        lowcost[k] = 0; //将当前顶点的权值设置为0，表示此顶点已经完成任务

        for (j = 1; j < G.numVertexes; j++)
        {
            if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) //若下标为k顶点各权值小于此前这些顶点未被加入生成树权值
            {
                lowcost[j] = G.arc[k][j]; //将较小权值存入lowcost
                adjvex[j] = k; //将下标为k的顶点存入adjvex
            }
        }
    }
}

我们来计算上文中连通网的最小生成树：

#include "CreateGraph.h"
#include "prim.h"

int main()
{
    MGraph G;
    CreateMgraph(&G);
    MinSpanTree_Prim(G);
    
    return 0;
}

注：CreateMgraph函数参考【数据结构】图的创建与遍历。

打印输出：

四、总结

普利姆算法是以某顶点为起点，逐步查找各顶点上最小权值的边来构建最小生成树的，对于边数非常多的稠密图计算效率较高，两个for循环嵌套可知，时间复杂度为$O(n^2)$。