制定一条最短的路径,要你旅行31个城市,每个城市只能经过一次并且最后要回到起点
MATLAB代码
tic
clear all;
close all;
clc;
C = [1304 2312; % 城市坐标
3639 1315;
4177 2244;
3712 1399;
3488 1535;
3326 1556;
3238 1229;
4196 1044;
4312 790;
4386 570;
3007 1970;
2562 1756;
2788 1491;
2381 1676;
1332 695;
3715 1678;
3918 2179;
4061 2370;
3780 2212;
3676 2578;
4029 2838;
4263 2931;
3429 1980;
3507 2376;
3394 2643;
3439 3201;
2935 3240;
3140 3550;
2545 2357;
2778 2826;
2370 2975];
% figure(1);
% scatter(C(:,1),C(:,2),'k','d');
% title('城市分布图');
[M,N] = size(C);
% M为问题的规模 M个城市
distance = zeros(M,M); % 用来记录任意两个城市之间的距离
% 求任意两个城市之间的距离
for m=1:M
for n=1:M
distance(m,n) = sqrt(sum((C(m,:)-C(n,:)).^2));
end
end
m = 50; % 蚂蚁的个数 一般取10-50
alpha = 1; % 信息素的重要程度 一般取【1,4】
beta = 5; % 启发式英子的重要程度 一般取【3,5】
rho = 0.25; % 信息素蒸发系数
G = 150;
Q = 100; % 信息素增加系数
Eta = 1./distance; % 启发式因子
Tau = ones(M,M); % 信息素矩阵 存储着每两个城市之间的信息素的数值
Tabu = zeros(m,M); % 禁忌表,记录每只蚂蚁走过的路程
gen = 1;
R_best = zeros(G,M); % 各代的最佳路线
L_best = inf.*ones(G,1); % 每一代的最佳路径的长度 初始假设为无穷大
% 开始迭代计算
while gen<G
% 将m只蚂蚁放到n个城市上
random_pos = [];
for i=1:(ceil(m/M)) % m只蚂蚁随即放到M座城市
random_pos = [random_pos,randperm(M)]; % random_pos=[1~31 + 1~31] 将每只蚂蚁放到随机的城市 在random_pos 中随机选择m个数,代表蚂蚁的初始城市
end
Tabu(:,1) = (random_pos(1,1:m))'; % 第一次迭代每只蚂蚁的禁忌表
for i=2:M % 从第二个城市开始
for j=1:m % 每只蚂蚁
visited = Tabu(j,1:(i-1)); % 在访问第i个城市的时候,第j个蚂蚁访问过的城市
% visited=visited(1,:);
unvisited = zeros(1,(M+1-i)); % 待访问的城市
visit_P = unvisited; % 蚂蚁j访问剩下的城市的概率
count = 1;
for k=1:M % 这个循环是找出未访问的城市
if isempty(find(visited==k)) %还没有访问过的城市 如果成立。则证明第k个城市没有访问过
unvisited(count) = k;
count = count+1;
end
end
% 计算待选择城市的概率
for k=1:length(unvisited) % Tau(visited(end),unvisited(k))访问过的城市的最后一个与所有未访问的城市之间的信息素
visit_P(k) = ((Tau(visited(end),unvisited(k)))^alpha)*(Eta(visited(end),unvisited(k))^beta);
end
visit_P = visit_P/sum(visit_P); % 访问每条路径的概率的大小
% 按照概率选择下一个要访问的城市
% 这里运用轮盘赌选择方法 这里也可以选择选择概率最大的路径去走, 这里采用轮盘赌选择法。
Pcum = cumsum(visit_P);
selected = find(Pcum>=rand);
to_visited = unvisited(selected(1));
Tabu(j,i) = to_visited; % 添加到禁忌表
end
end
if gen>=2
Tabu(1,:) = R_best(gen-1,:);
end
% 记录m只蚂蚁迭代的最佳路线
L = zeros(1,m);
for i=1:m
R = Tabu(i,:);
L(i) = distance(R(M),R(1)); % 因为要走一周回到原来的地点
for j=1:(M-1)
L(i) = L(i)+distance(R(j),R(j+1));
end
end
L_best(gen) = min(L); % 记录每一代中路径的最短值
pos = find(L==L_best(gen));
R_best(gen,:) = Tabu(pos(1),:); % 最优的路径
% 更新信息素的值
Delta_Tau = zeros(M,M);
for i=1:m % m只蚂蚁
for j=1:(M-1) % M座城市
Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = Delta_Tau(Tabu(i,j),Tabu(i,j+1)) + Q/L(i); % m只蚂蚁的信息素累加 这里采用的是论文中ant-cycle模型
end
Delta_Tau(Tabu(i,M),Tabu(i,1)) = Delta_Tau(Tabu(i,M),Tabu(i,1)) + Q/L(i);
end
Tau = (1-rho).*Tau+Delta_Tau; % 更新路径上的信息素含量
% 禁忌表清零
Tabu = zeros(m,M);
for i=1:(M-1)
plot([C(R_best(gen,i),1),C(R_best(gen,i+1),1)],[C(R_best(gen,i),2),C(R_best(gen,i+1),2)],'bo-');
hold on;
end
plot([C(R_best(gen,n),1),C(R_best(gen,1),1)],[C(R_best(gen,n),2),C(R_best(gen,1),2)],'ro-');
title(['最短路径:',num2str(L_best(gen))]);
hold off;
pause(0.05);
gen = gen+1;
end
figure(2);
plot(L_best);
title('路径长度变化曲线');
xlabel('迭代次数');
ylabel('路径长度数值');
toc
计算结果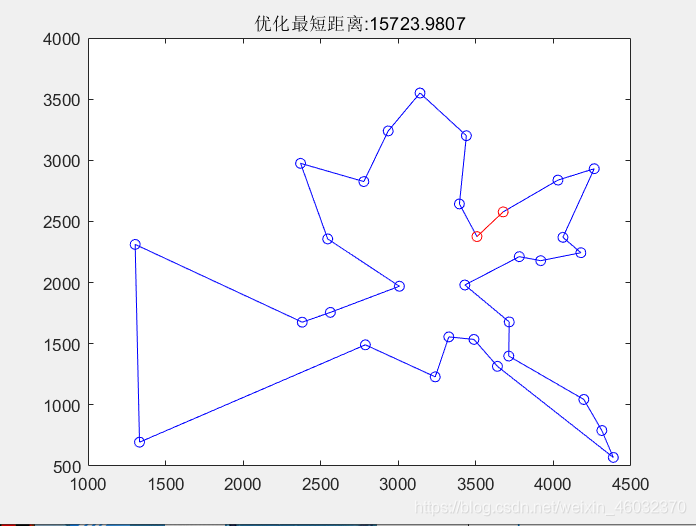
版权声明:本文为weixin_46032370原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。