数字信号处理:研究时域离散的模拟信号
一、离散信号与系统
1.离散的基本概念
模拟信号与数字信号从纵轴幅值上分析
连续信号与离散信号从横轴时间上分析
狭义模拟信号:时间连续,幅值连续
时域离散信号:时间离散,幅值连续(t\特殊模拟信号)
狭义数字信号:时间离散,幅值离散
幅度离散信号:时间连续,幅值离散(特殊数字信号)
系统的目的就是对信号进行变换、处理的
连续系统:由加法器、乘法器、积分器组成,信号波形发送变化
离散系统:由加法器、乘法器、延时器组成,信号序列发送变化
2.频谱基本概念
信号的频谱(or频谱密度函数)
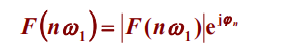
F ( n w 1 ) 频 谱 F(nw1)频谱F(nw1)频谱
∣ F ( n w 1 ) ∣ 幅 频 特 性 ( 幅 度 频 率 特 性 ) 、 幅 度 谱 ( 幅 度 频 谱 图 ) |F(nw1)|幅频特性(幅度频率特性)、幅度谱(幅度频谱图)∣F(nw1)∣幅频特性(幅度频率特性)、幅度谱(幅度频谱图)
φ n 相 频 特 性 ( 相 位 频 率 特 性 ) 、 相 位 谱 ( 相 位 频 谱 图 ) \varphi_n相频特性(相位频率特性)、相位谱(相位频谱图)φn相频特性(相位频率特性)、相位谱(相位频谱图)
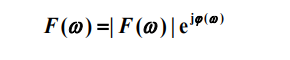
F ( w ) 频 谱 密 度 函 数 , 简 称 频 谱 函 数 F(w)频谱密度函数,简称频谱函数F(w)频谱密度函数,简称频谱函数
∣ F ( w ) ∣ 幅 频 特 性 ( 幅 度 频 率 特 性 ) 、 幅 度 谱 ( 幅 度 频 谱 图 ) |F(w)|幅频特性(幅度频率特性)、幅度谱(幅度频谱图)∣F(w)∣幅频特性(幅度频率特性)、幅度谱(幅度频谱图)
φ ( w ) 相 频 特 性 ( 相 位 频 率 特 性 ) 、 相 位 谱 ( 相 位 频 谱 图 ) \varphi(w)相频特性(相位频率特性)、相位谱(相位频谱图)φ(w)相频特性(相位频率特性)、相位谱(相位频谱图)
系统频谱
单位冲击响应h(t)或h(n)
连续信号的系统函数H ( s ) H(s)H(s)
频率响应特性(函数)H ( j w ) H(jw)H(jw)
H ( j w ) = ∣ H ( j w ) ∣ φ ( w ) H(jw)=|H(jw)|\varphi(w)H(jw)=∣H(jw)∣φ(w)
∣ H ( j w ) ∣ 幅 频 特 性 , φ ( w ) 相 频 特 性 |H(jw)|幅频特性,\varphi(w)相频特性∣H(jw)∣幅频特性,φ(w)相频特性
离散信号的系统函数H ( z ) H(z)H(z)
频率响应特性(函数)H ( e j w ) H(e^{jw})H(ejw)
H ( e j w ) = H g ( w ) e j θ ( w ) H(e^{jw})=H_g(w)e^{j\theta(w)}H(ejw)=Hg(w)ejθ(w)
H g ( w ) 幅 度 特 性 ( 振 幅 响 应 ) , θ ( w ) 相 位 特 性 ( 相 位 响 应 ) H_g(w)幅度特性(振幅响应),\theta(w)相位特性(相位响应)Hg(w)幅度特性(振幅响应),θ(w)相位特性(相位响应)

3.卷积
连续卷积
理解卷积:
f(τ \tauτ)是τ \tauτ时刻吃到肚子里面的东西
h(t-τ \tauτ),τ \tauτ时刻吃的东西在t时刻剩余的比例
f(τ \tauτ)h(t-τ \tauτ),τ \tauτ时刻吃的东西在t时刻剩余的量
f(t)卷积h(t):在t时刻肚子里食物量
h(t)是一个系统函数,0时刻吃的东西,在肚子里t时刻剩余函数的比例
计算卷积:
交叉相乘:先翻转,再平移t后乘积的积分
离散线性卷积(卷积和)

离散循环卷积(圆周卷积)




二、离散傅里叶变换
1.理想采样信号的傅里叶变换(FT)
1.1 原模拟信号:傅里叶变换结果的横坐标Ω 或 f \Omega 或fΩ或f
模拟角频率Ω = 2 π f \Omega=2 \pi fΩ=2πf——信号带限频率Ω c \Omega_cΩc
模拟频率(线频率)f ff——信号带限频率f c f_cfc或f m a x f_{max}fmax
注:数字信号没有线频率
1.2 模拟周期冲击信号:
采样周期T s T_sTs(或T)——周期冲击信号的周期
采样角频率Ω s = 2 π T s \Omega_s=\frac{2\pi}{T_s}Ωs=Ts2π——周期冲击信号模拟角频率
采样频率f s 或 F s = 1 T s f_s或F_s=\frac{1}{T_s}fs或Fs=Ts1——周期冲击信号的模拟频率。
注:F s / 2 F_s/2Fs/2折叠频率
1.3 理想采样信号:一般模拟信号,只能FT得到横轴Ω 或 f \Omega或fΩ或f
理想采样信号=原模拟信号乘以周期冲击信号
理想采样信号x a ( t ) − \overset{-}{x_a(t)}xa(t)−是对连续模拟信号采样: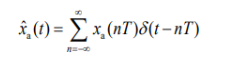
1.4 周期冲击信号的FT与理想采样信号的FT
利用时域相乘频域卷积的方法求理想采样信号的傅里叶变换
1.5 时域离散信号的FT(横轴换成w即DTFT)
时域离散信号:特殊模拟信号
这里采样直接对时域离散信号傅里叶变换

结论:理想采样信号FT与时域离散信号DTFT 等价
上一讲得到理想采样信号的连续傅里叶变换(FT)的频谱是模拟信号频谱周期性延拓
这一讲得到时域离散信号的离散傅里叶变换(DTFT)的频谱也是模拟信号频谱周期性延拓
2.离散非周期信号的离散时间傅里叶变换(DTFT)
 时域离散信号x ( n ) x(n)x(n):
时域离散信号x ( n ) x(n)x(n):
横轴为nT省略成n,纵轴为x(nT)省略成x(n)
数字域频率w = Ω T s = Ω F s = 2 π f f s w= \Omega T_s=\frac{\Omega}{F_s}=2 \pi\frac{ f}{f_s}w=ΩTs=FsΩ=2πfsf,归一化频率范围【 0 , 2 π 】 【0,2\pi】【0,2π】
时域离散信号的周期为N NN,满足x ( n ) = x ( n + N ) x(n)=x(n+N)x(n)=x(n+N)
即 x ( w 0 n ) = x ( w 0 ( n + N ) ) 即x(w_0n)=x(w_0(n+N))即x(w0n)=x(w0(n+N))
w 0 N 是 2 π 的 整 数 倍 , w 0 N = 2 π k w_0N是2\pi的整数倍,w_0N=2\pi kw0N是2π的整数倍,w0N=2πk
即 N T = 2 π Ω k 即NT=\frac{2\pi}{\Omega}k即NT=Ω2πk
采 样 信 号 的 模 拟 周 期 是 原 模 拟 信 号 周 期 的 k 倍 采样信号的模拟周期是原模拟信号周期的k倍采样信号的模拟周期是原模拟信号周期的k倍
过 了 N 个 点 波 形 重 复 过了N个点波形重复过了N个点波形重复
3.离散周期信号的傅里叶级数(DFS)

4.离散周期信号离散时间傅里叶变换(DTFT)

4.1基本序列的傅里叶变换

4.2复指数信号的离散时间傅里叶变换

5.离散傅里叶变换(DFT):与DFS密切相关

5.1 时域采样定理(奈奎斯特采样定理或奈奎斯特定理)
| 横轴 | 横轴起点 | 检测的最高频率成分 | 一个周期终点 | 信号实际包含的最高成分 |
|---|---|---|---|---|
| 模 拟 角 频 率 Ω = 2 π f 模拟角频率\Omega=2\pi f模拟角频率Ω=2πf | 0 | Ω s / 2 \Omega_s/2Ωs/2 | Ω s = 2 π T s \Omega_s=\frac{2\pi}{T_s}Ωs=Ts2π | 信 号 带 限 频 率 Ω c 信号带限频率\Omega_c信号带限频率Ωc |
| 模 拟 频 率 f = Ω 2 π 模拟频率f=\frac{\Omega}{2\pi}模拟频率f=2πΩ | 0 | f s / 2 , 折 叠 频 率 f_s/2,折叠频率fs/2,折叠频率 | f s = 1 T s f_s=\frac{1}{T_s}fs=Ts1 | 信 号 带 限 频 率 f c 信号带限频率\ f _c信号带限频率 fc |
| 数 字 域 频 率 w = Ω T s = 2 π f f s 数字域频率w=\Omega T_s=2\pi\frac{f}{f_s}数字域频率w=ΩTs=2πfsf | 0 | π \piπ | 2π \piπ | 2 π f c f s 2\pi \frac{f_c}{f_s}2πfsfc |
| 归 一 化 数 字 频 率 归一化数字频率归一化数字频率 | 0 | 1 11 | 2 22 | 2 f c f s 2 \frac{f_c}{f_s}2fsfc |
原理:
时域连续非周期的信号x ( t ) x(t)x(t)通过FT得到频域非周期连续F ( j Ω ) F(j\Omega)F(jΩ)
时域离散非周期的理想采样信号x ( t ) ′ x(t)'x(t)′通过FT得到频域周期连续的X ( j Ω ) ′ X(j\Omega)'X(jΩ)′
时域离散非周期的时域离散信号x ( n ) x(n)x(n)通过DTFT得到频域周期连续X ( e j w ) X(e^{jw})X(ejw)
理解:
研究能否通过采样后的x ( t ) ′ x(t)'x(t)′或x ( n ) x(n)x(n)恢复x(t)
即研究能不能通过周期连续的频谱X ( j Ω ) ′ X(j\Omega)'X(jΩ)′或X ( e j w ) X(e^{jw})X(ejw)恢复非周期连续的频谱F ( j Ω ) F(j\Omega)F(jΩ)
即研究x ( t ) ′ x(t)'x(t)′或x ( n ) x(n)x(n)通过低通滤波器能否恢复成x(t)
结论:
如果采样点数少,可能发生频谱混叠,x(n)无法恢复x(t)
条件如下:
连续非周期信号的持续时间T p T_pTp一定
采样间隔T s T_sTs越小,采样点数M越多,采样频率f s f_sfs越高
采样周期T s T_sTs足够小
采样频率足够大F s 2 > f m a x \frac{F_s}{2}>f_{max}2Fs>fmax即f s > 2 f c f_s>2f_cfs>2fc
采样角频率足够大Ω s ≥ 2 Ω c \Omega_s\ge2\Omega_cΩs≥2Ωc
时域采样定理的内插公式:
频域通过乘以低通滤波器恢复
即时域通过卷积低通滤波器时域表达式sa函数恢复
5.2 频域采样定理:
原理:
时域连续非周期的信号x ( t ) x(t)x(t)通过FT得到频域非周期连续F ( j Ω ) F(j\Omega)F(jΩ)
时域离散非周期的理想采样信号x ( t ) ′ x(t)'x(t)′通过FT得到频域周期连续的X ( j Ω ) ′ X(j\Omega)'X(jΩ)′
时域离散非周期的时域离散信号M点x ( n ) x(n)x(n)通过DTFT得到频域周期连续X ( e j w ) X(e^{jw})X(ejw),周期2 π ( 归 一 化 ) 2\pi(归一化)2π(归一化)
M点时域离散x ( n ) x(n)x(n)以N为周期延拓x N ( n ) x_N(n)xN(n),DFS得到以N为周期的频域离散X N ( k ) X_N(k)XN(k)
时域离散非周期的M点x ( n ) x(n)x(n)通过N点DFT得到频域非周期离散N点X ( k ) X(k)X(k)
——DFT由DFS截取N点主值序列
——X ( k ) X(k)X(k)是对连续频谱X ( e j w ) X(e^{jw})X(ejw)一个2 π 2\pi2π周期做N点等间隔采样得到
理解:
研究能否通过采样后的X ( k ) X(k)X(k)恢复连续的频谱X ( e j w ) X(e^{jw})X(ejw)一个2 π 2\pi2π区间
即研究能否通过采样后的X N ( k ) X_N(k)XN(k)恢复连续的频谱X ( e j w ) X(e^{jw})X(ejw)全区间
即研究能否通过x N ( n ) x_N(n)xN(n)恢复M点x ( n ) x(n)x(n)
即研究x N ( n ) x_N(n)xN(n)的截取N点主值序列是不是M点x ( n ) x(n)x(n)
结论:
如果发生时域混叠,则X ( k ) X(k)X(k)无法恢复频谱X ( e j w ) X(e^{jw})X(ejw)
条件如下:
连续非周期信号的采样时间T p T_pTp一定,频率分辨率一定,同时采样间隔一定即采样点数就为M点,
进行DFT的点数N越多,在频域上的采样点数N越多
DFT点数N>=信号有效点数M——IDFT的结果即X N ( k ) ′ X_N(k)'XN(k)′主值序列就是x(n),无时域混叠
频域采样定理的内插公式:
时域通过截取主值序列恢复
即时域通过乘以矩形窗恢复,频域通过卷积sa函数进行恢复
5.3 为什么有DFT?
连续非周期信号x ( t ) x(t)x(t):FT连续非周期的频谱密度函数F ( w ) F(w)F(w)
问题1:FT不行,计算机无法输入的连续时域信号
——计算机可以输入采样的非周期离散信号x ( n ) : x(n):x(n):DTFT是F(w)周期延拓或DTFT得到连续周期频谱密度函数X ( e j w ) X(e^{jw})X(ejw)
问题2:x(n)可以无失真恢复x(t)吗?
——可以,满足时域采样定理
问题3:FT/DTFT不行,计算机依然无法输出周期连续的频谱
——非周期离散信号周期延拓得到x ˇ ( n ) \check x(n)xˇ(n):DFS离散周期的频谱密度函数X ˇ ( k ) \check X(k)Xˇ(k)
注:DFS的傅里叶级数没有1/N,X(k)是频谱密度函数不是频谱,就是让X(k)直接变成连续信号的采样)
问题4:X ˇ ( k ) \check X(k)Xˇ(k)能够恢复出X ( e j w ) X(e^{jw})X(ejw)吗?
——可以,频域采样定理
问题5:DFS不行,计算机无法输入输出都是无限长的
——非周期离散信号周期傅里叶级数时域和频域截取主值序列即DFT
DFS是对DTFT的在每个2 π 2\pi2π区间上的N点等间隔采样
DFT是对DFS的时域和频域取主值序列N个点
5.4 DFT误差分析
5.4.1 有效采样点数M
1.时域信号长度T p TpTp一定,只缩短采样周期来增加原信号有效采样点数M
——T p TpTp一定,即频率分辨率不变
——采样频率不够大,频域混叠
——理想采样信号频谱延拓,Ω s 、 f s \Omega_s、f_sΩs、fs持续增加,检测信号的不同的频率成分越多,信号的真实频谱范围增加DFT低频信号带宽占0 到 2 π 0到2\pi0到2π范围减小,0 到 2 π 0到2\pi0到2π反映的信号频率成分更全面(归一化反映不是真实的信号频率)
2.采样频率不变,增加信号持续时间T p T_pTp增加原信号有效采样点数M
——信号截断效应缓解,信号M大则截止频率越小
——采样频率一定,频域延拓周期一样,信号越长频域采样点数越多,频率分辨率自然高
有效采样点数M = T p T s = T p f s M=\frac{T_p}{T_s}=T_pf_sM=TsTp=Tpfs
频率分辨率F ( 单 位 H z ) = f s M = 1 M T s = 1 T p F(单位Hz)=\frac{f_s}{M}=\frac{1}{MT_s}=\frac{1}{T_p}F(单位Hz)=Mfs=MTs1=Tp1
注:
时间分辨率高是采样周期小
频率分辨率F是对模拟信号频谱的采样间隔,只和T p T_pTp有关,越接近真实频谱,频率分辨率越高
5.4.2 频域采样点数N
1.N不够大,时域混叠
时域采样周期不变,给信号补零来增加信号DFT在频域采样点数N
2.采样间隔T不变,理想采样信号频谱不搬移,没有让反映信号的频率成分更全面。
3.DFT连续频谱频域N点等间隔采样,即补零的周期延拓使得N越大,这一段频率更靠近连续谱了,减小栅栏效应,增加了观察分辨率。
4.频率分辨率有没有提高不一定。若数据在补零位置就是0确实提高了频率分辨率,但数据在补零位置不是零,我们的频谱逼近的是在补零位置为0的连续频谱,故频率分辨率没有提高,即也许出现截断效应那么频率无法完善。补零点得到的是高密度频谱,并不能得到高分辨率谱,要提高频率分辨率,则要通过增加数据记录长度来提高物理分辨率。
5.4.3 频谱混叠、截断效应、栅栏效应:
时域抽样——频谱混叠:
进行预滤波(抗混叠滤波器)
增加采样频率,f s > = 2 f c f_s>=2f_cfs>=2fc,增加频谱搬移程度
时域截断——截断效应(频谱泄露、干扰):
增大窗函数长度M
增大截取的有效采样点数M
增大截取信号长度Tp
增大频率分辨率F
频谱变宽拖尾振荡
非周期信号很长,就需要窗函数截取非周期信号的一段
频域卷积窗函数,时域乘以sa函数,sa函数要用窗截取
窗有矩形窗、三角窗、二阶升余弦窗、汉明窗、海宁窗、布莱克曼窗
频域抽样——时域混叠:
增大频域采样点数N使满足:
频域采样点数N>截取的信号点数M
频域抽样——栅栏效应
非周期信号当成周期信号,频域从连续谱变成离散谱,肯定存在栅栏效应
补零使得频域采样点数N越大,观察分辨率越高
减小截断效应,即增大窗函数长度增大频率分辨率
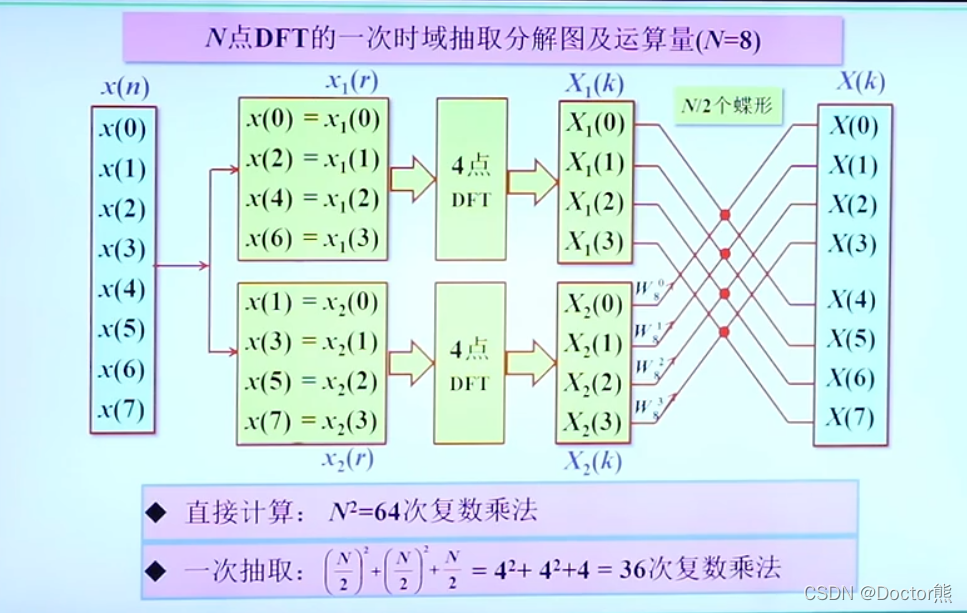
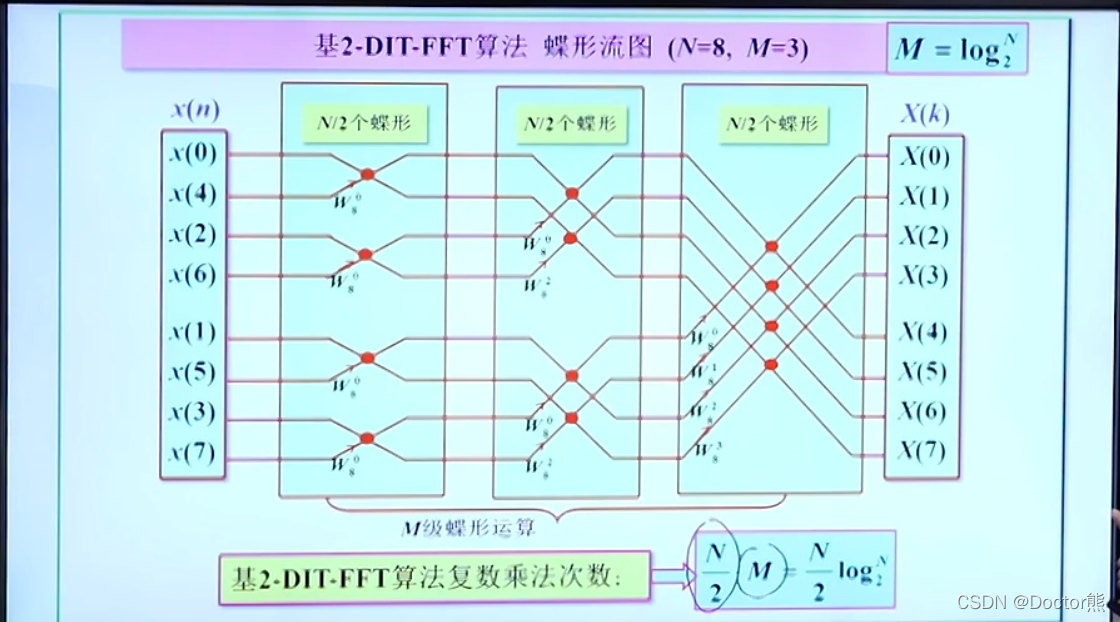
6. 快速傅里叶变换(FFT与IFFT)
matlab应用:FFT与IFFT
N点DFT的运算量: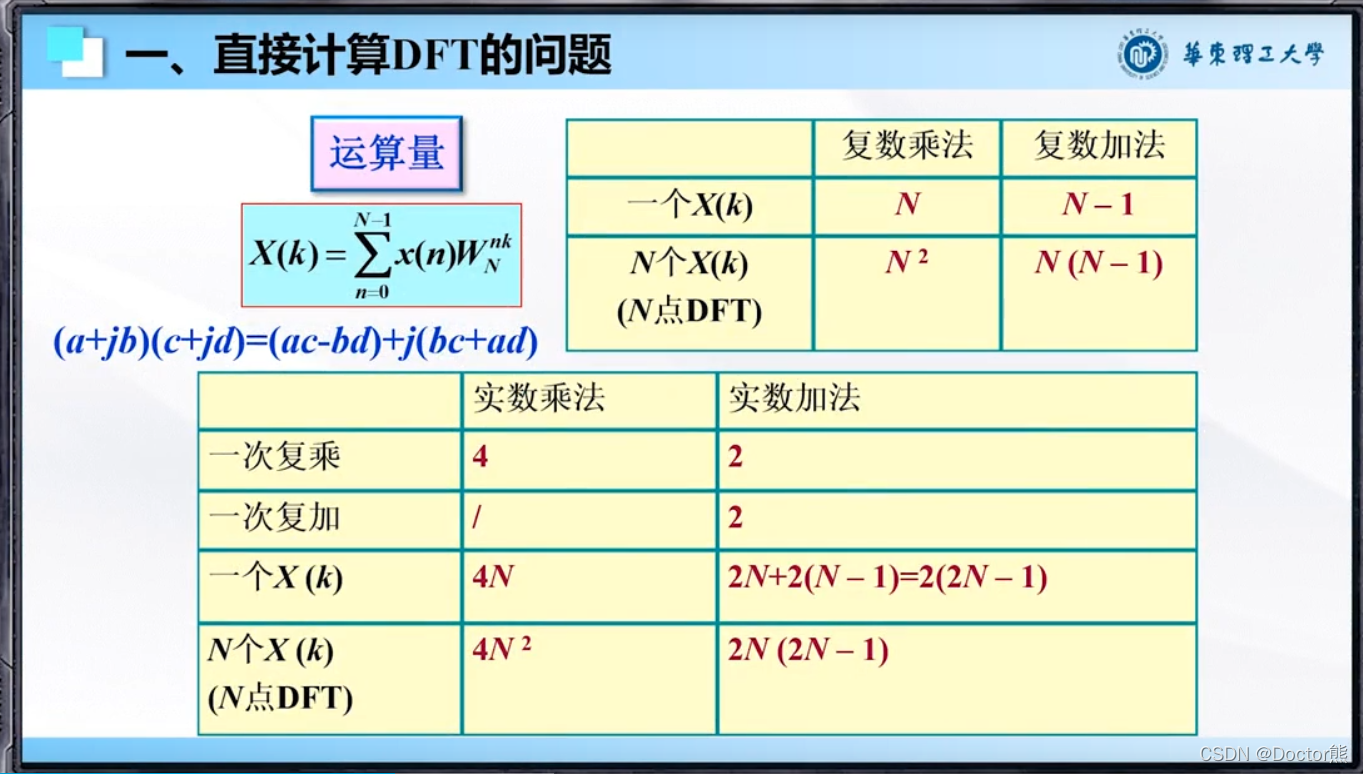


三、z变换
z变换是将信号做不同常数级衰减之后再进行离散时间傅里叶变换
在单位圆外说明需要衰减,在单位圆内说明扩大都没事!
DTFT傅里叶变换与z变换

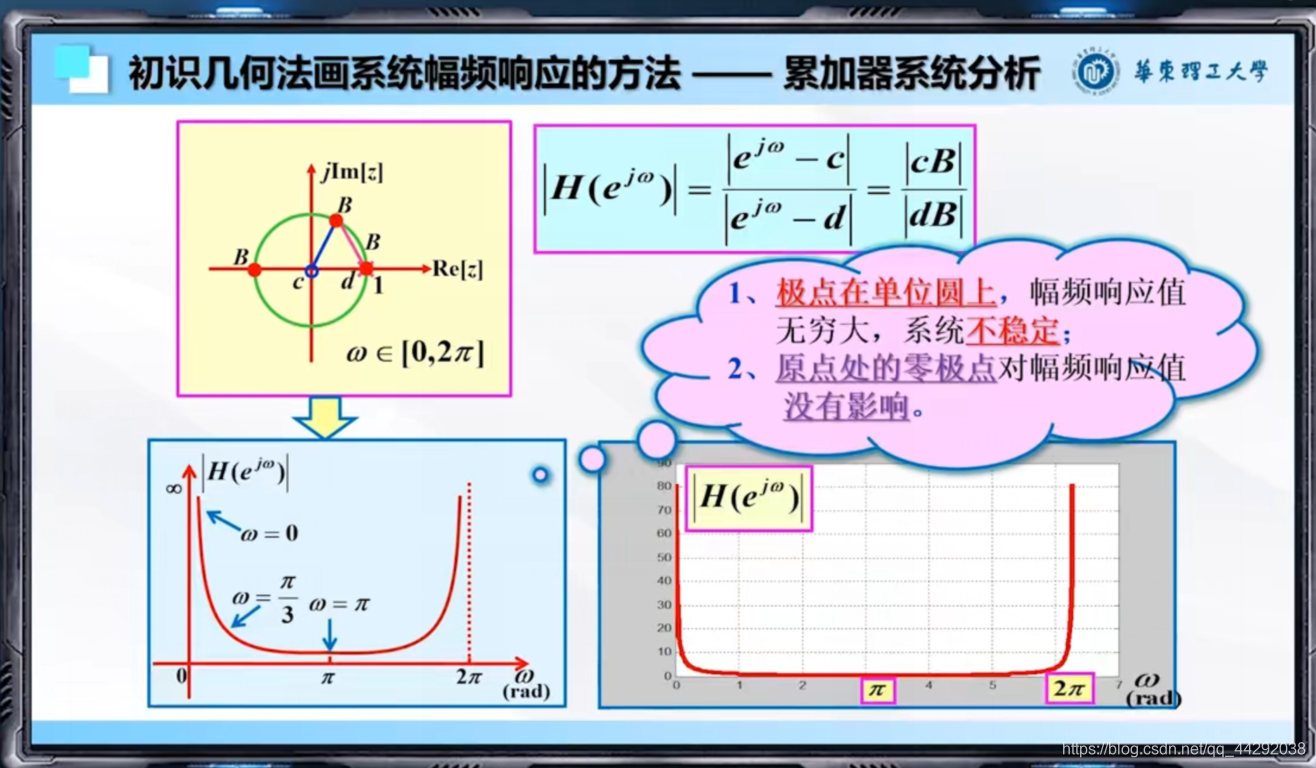
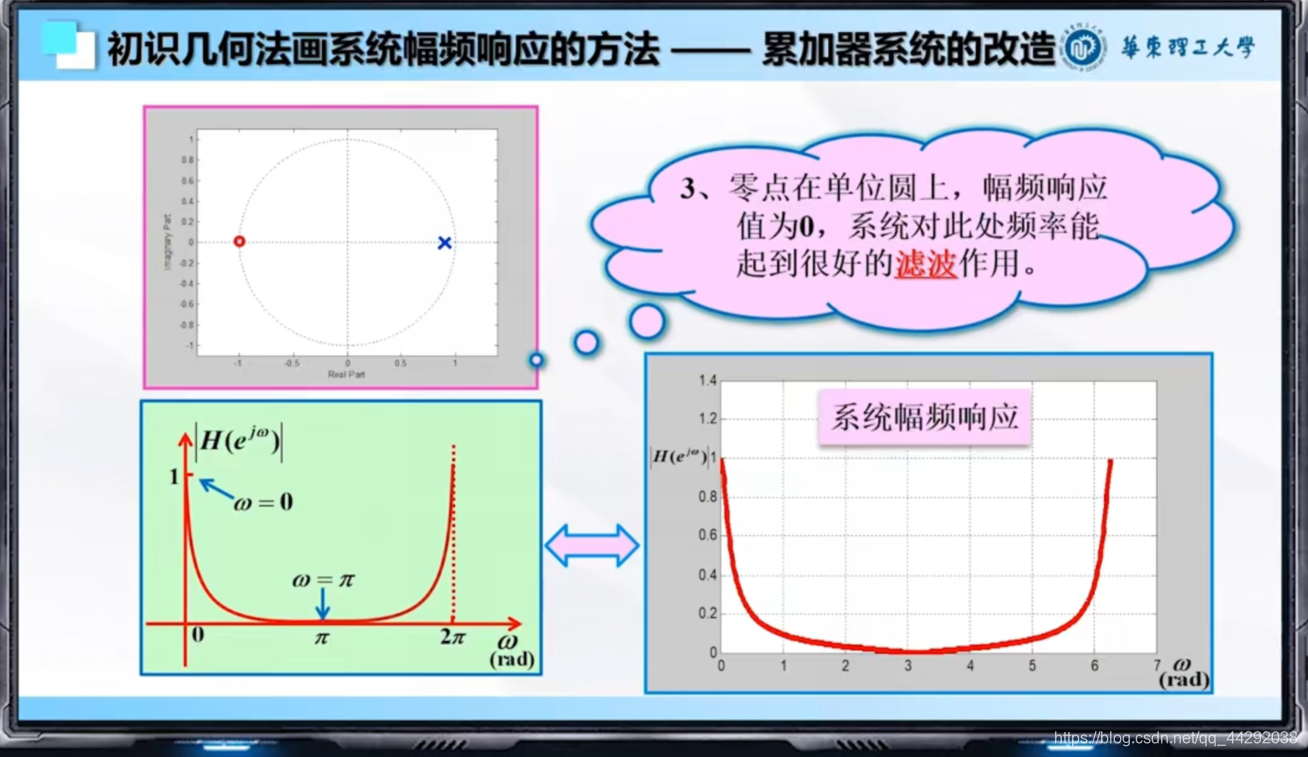
零极点分布与幅频特性
H ( e j w ) H(e^{jw})H(ejw)变换成零极点类型,根据零极点大致判断H ( e j w ) H(e^{jw})H(ejw)的幅频特性曲线
e j w e^{jw}ejw是在复平面单位圆上移动的点,从0到2 π 一 次 循 环 2\pi一次循环2π一次循环
分子变成零点矢量,由零点指向单位圆上的点
分母变成极点矢量,由极点指向单位圆上的点

线性相位FIR零极点分布的特点
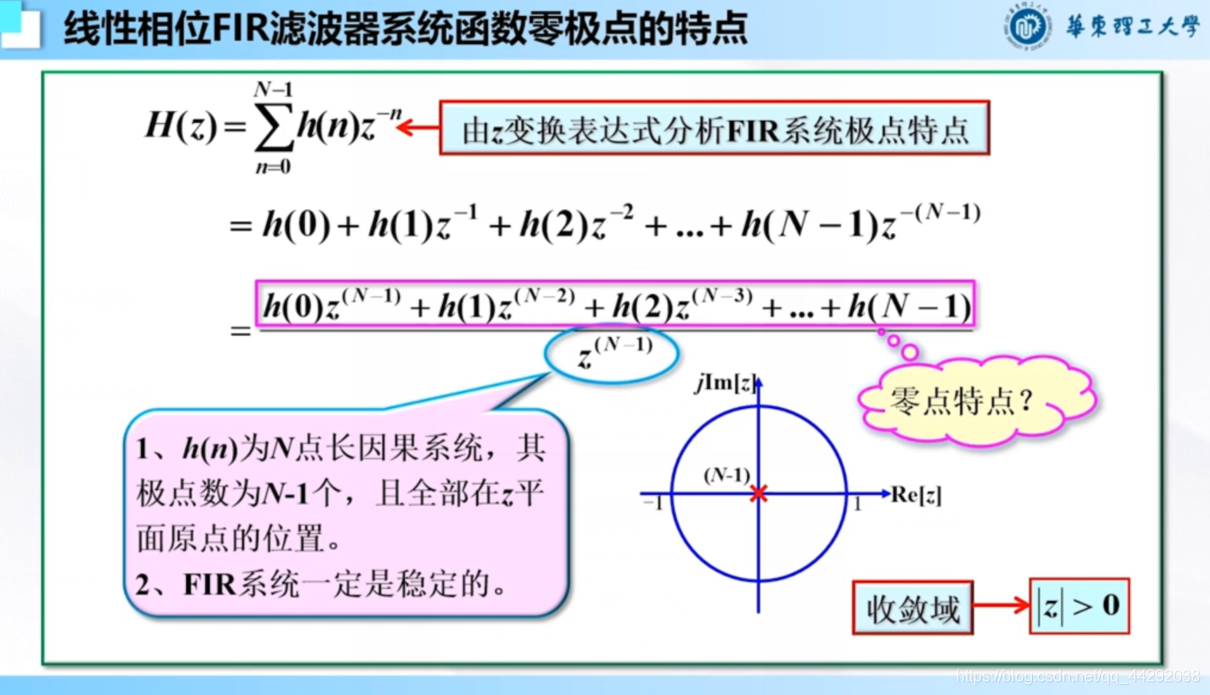

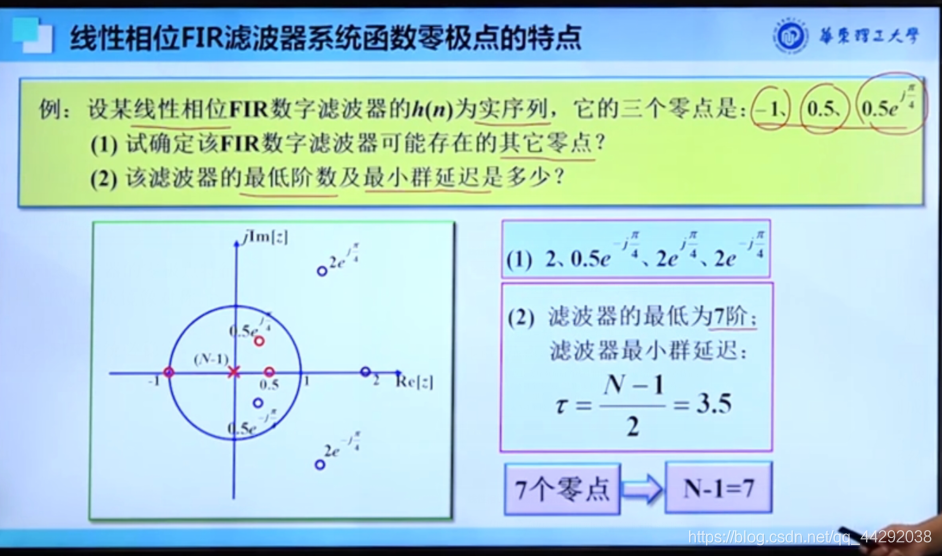
四、手工滤波器设计
模拟滤波器、数字滤波器
低通滤波器、高通滤波器、带通滤波器、带阻滤波器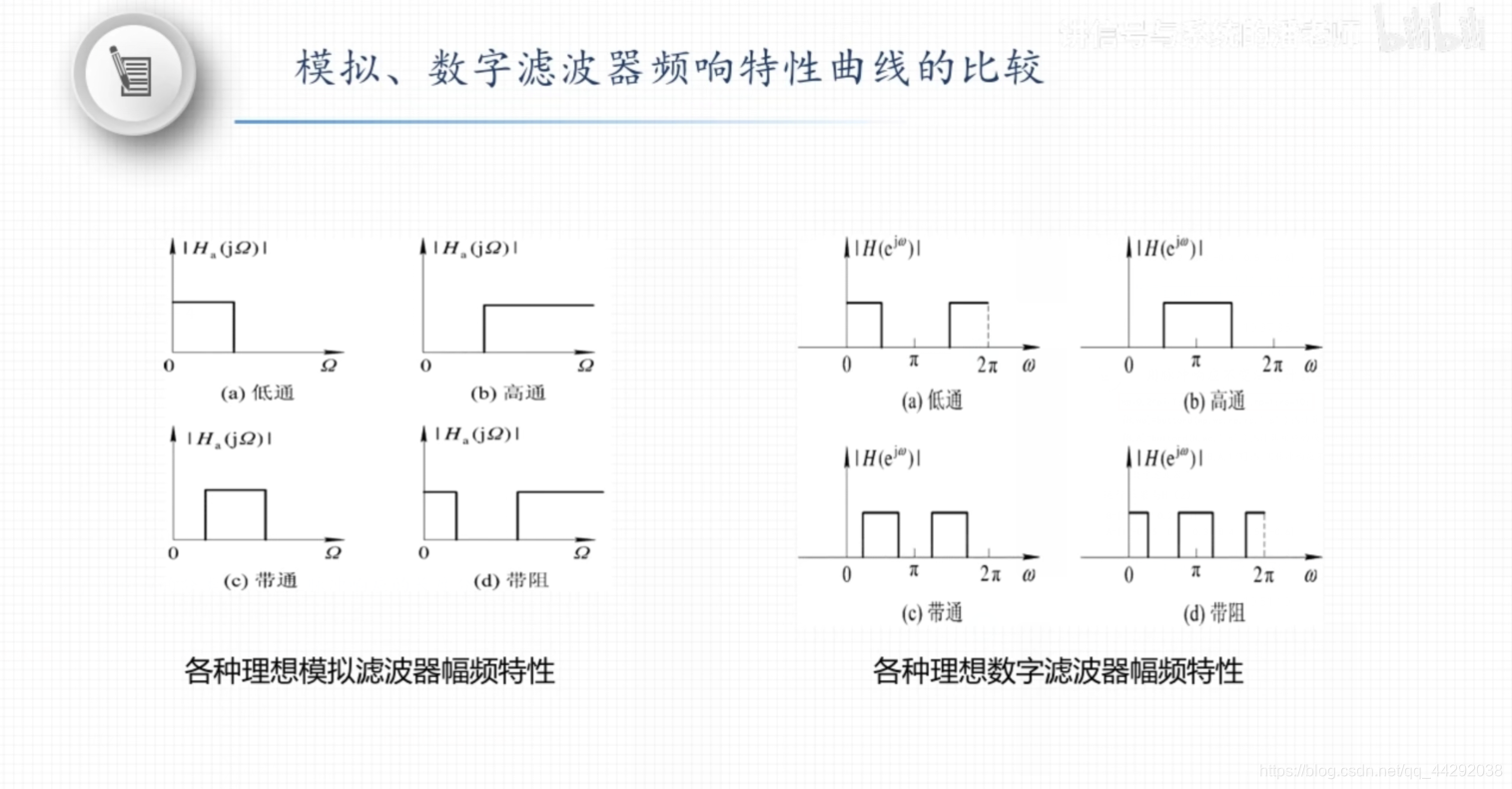
1.模拟滤波器设计
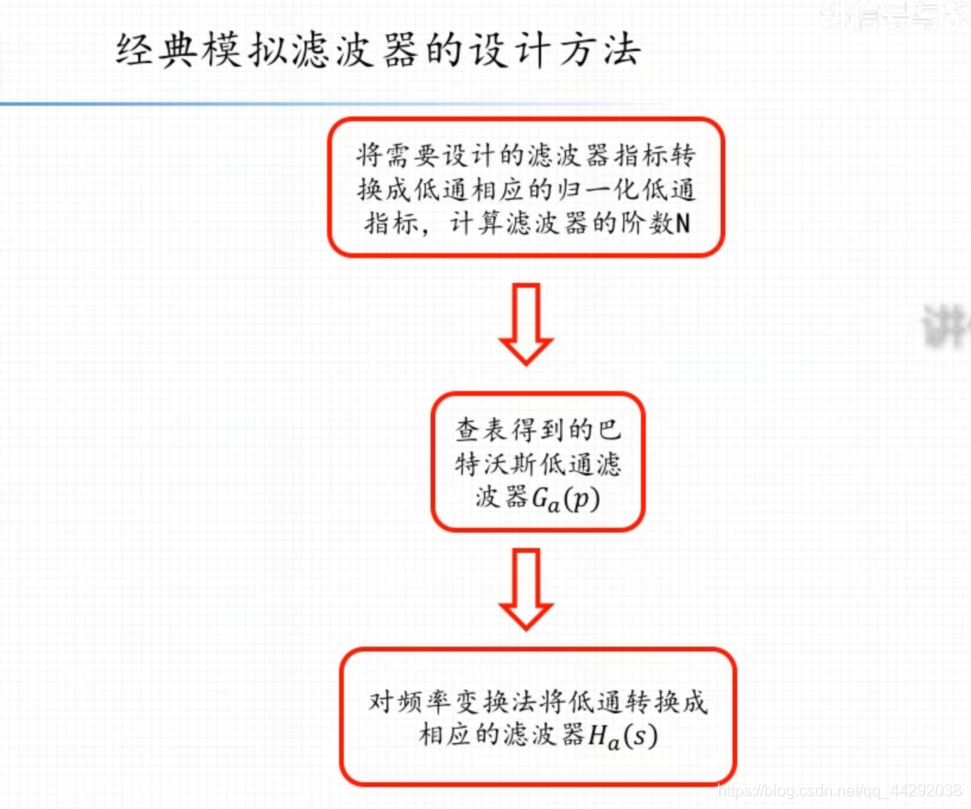
模拟滤波器设计方法:
巴特沃斯滤波器:通带平坦,单调下降的幅频特性
切比雪夫滤波器:通带或阻带具有等波纹特性
椭圆滤波器:通带具有等波纹特性
贝塞尔滤波器:通带具有线性相位特性
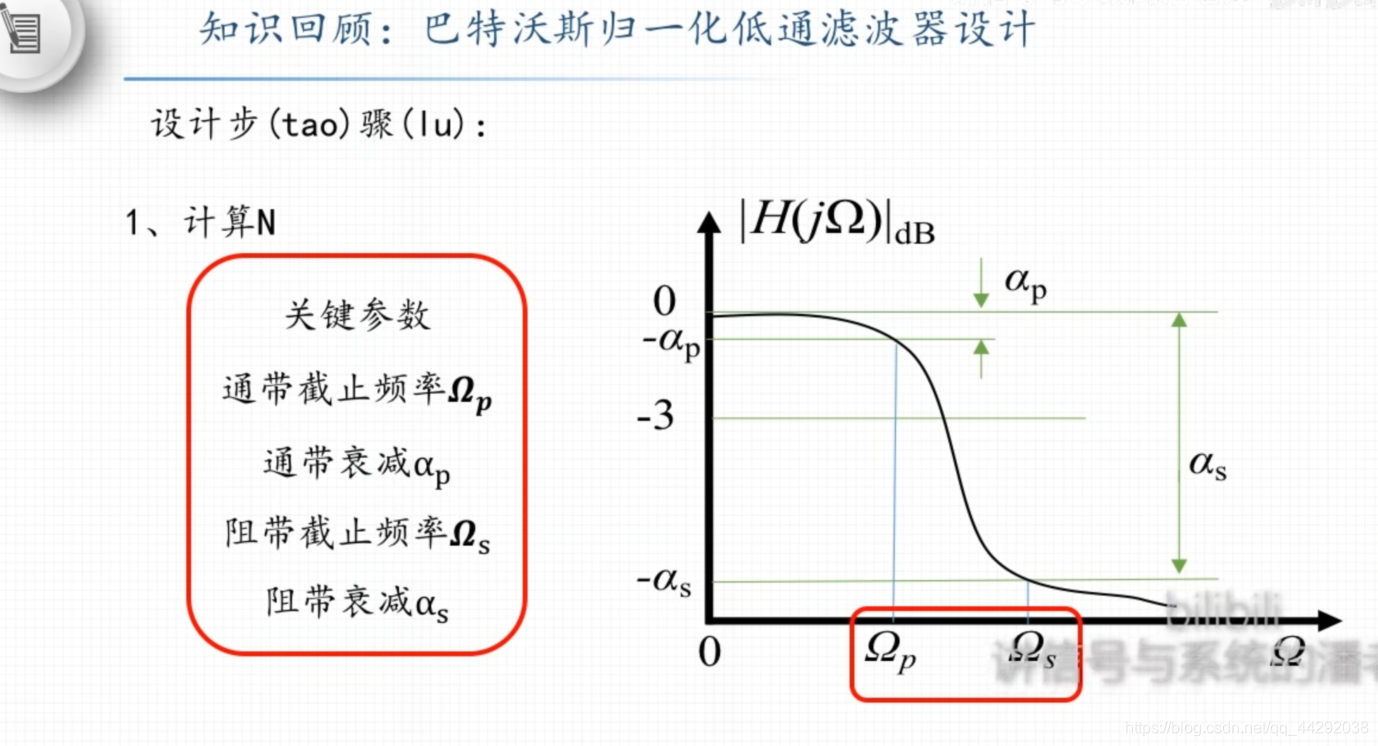
设计指标
Ω p 通 带 边 界 频 率 \Omega_p通带边界频率Ωp通带边界频率,α p 通 带 最 大 衰 减 , 即 幅 度 下 降 α p \alpha_p通带最大衰减,即幅度下降\alpha_pαp通带最大衰减,即幅度下降αp
——通带衰减不能超过这个指标
Ω s 阻 带 截 止 频 率 \Omega_s阻带截止频率Ωs阻带截止频率,α s 阻 带 最 小 衰 减 , 即 幅 度 下 降 α s \alpha_s阻带最小衰减,即幅度下降\alpha_sαs阻带最小衰减,即幅度下降αs
——阻带衰减必须超过这个指标
Ω c 是 3 d B 频 率 , 幅 度 下 降 到 2 2 , 功 率 下 降 了 一 半 \Omega_c 是3dB频率,幅度下降到\frac{\sqrt[]{2}}{2},功率下降了一半Ωc是3dB频率,幅度下降到22,功率下降了一半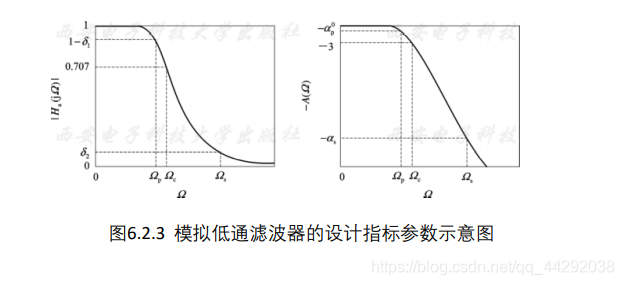

设计巴特沃斯低通滤波器的一般步骤与实例





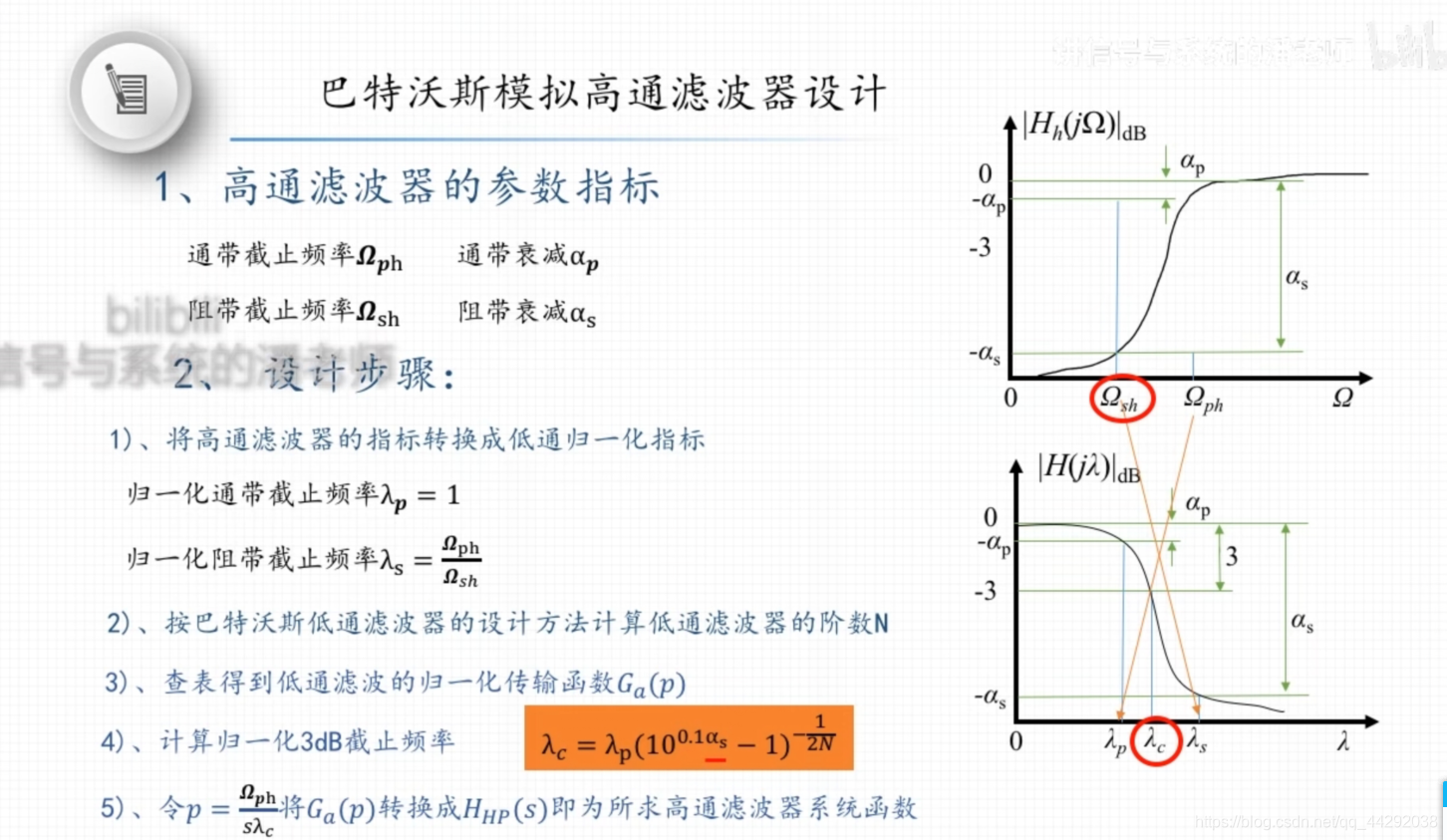
利用巴特沃斯模拟低通滤波器设计模拟高通滤波器



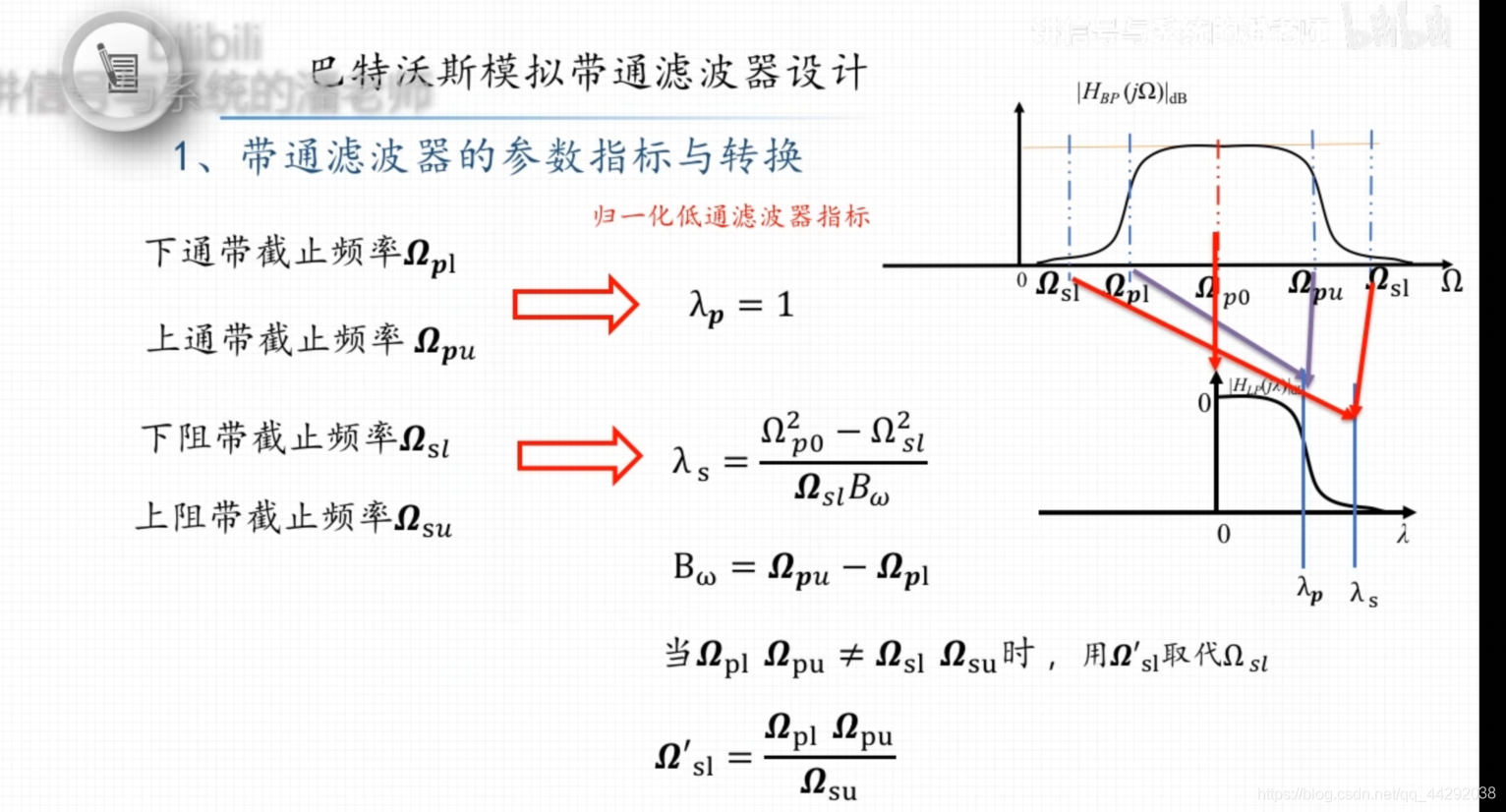
利用巴特沃斯模拟低通滤波器设计模拟带通滤波器






2.数字滤波器设计
数字滤波器设计方法:
无限长单位脉冲响应IIR滤波器、有限长单位脉冲响应FIR滤波器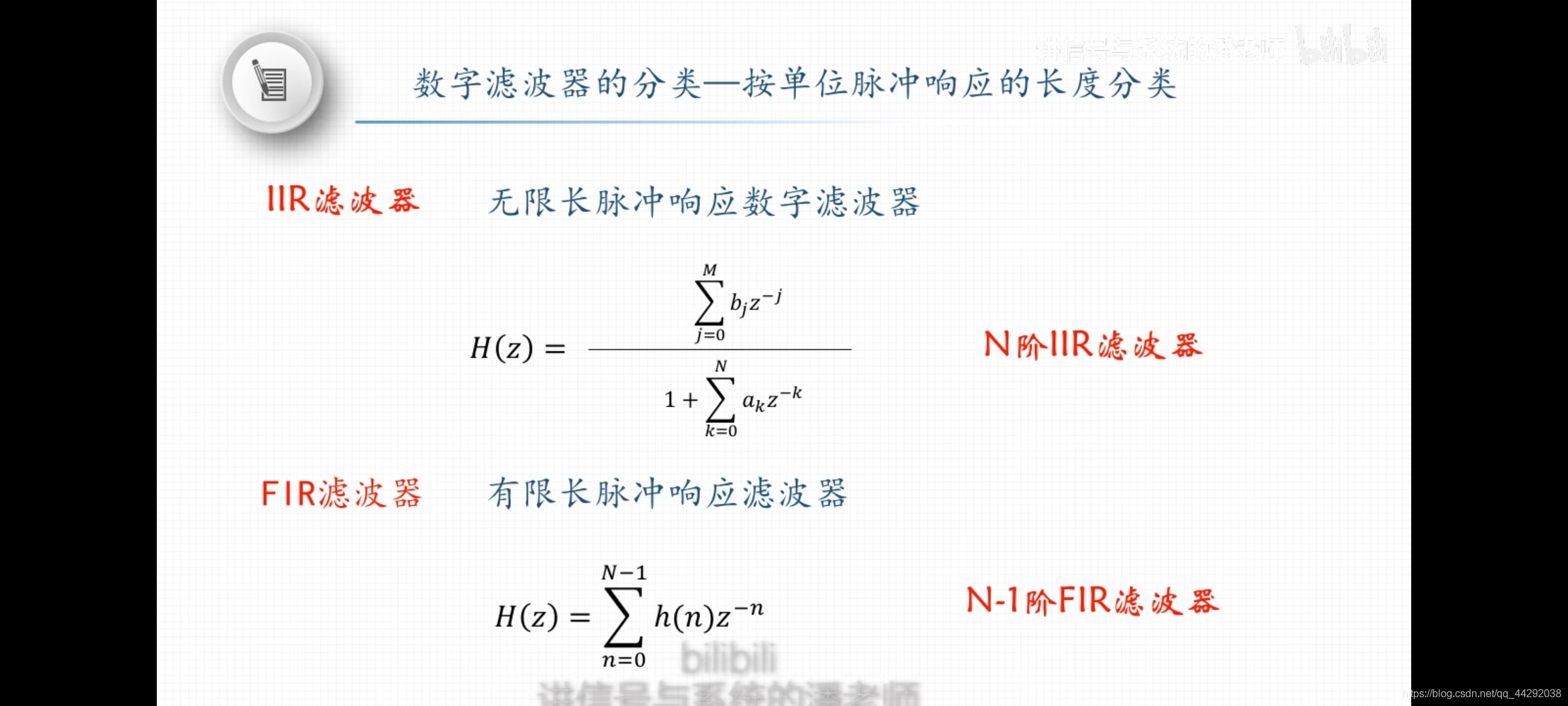

2.1 IIR滤波器设计(典型设计需要变换)

例1:设计IIR数字低通滤波器-脉冲响应不变法
脉冲响应不变法是利用z变换与拉普拉斯变换之间的对应关系,但是要转换为零极点增益模型



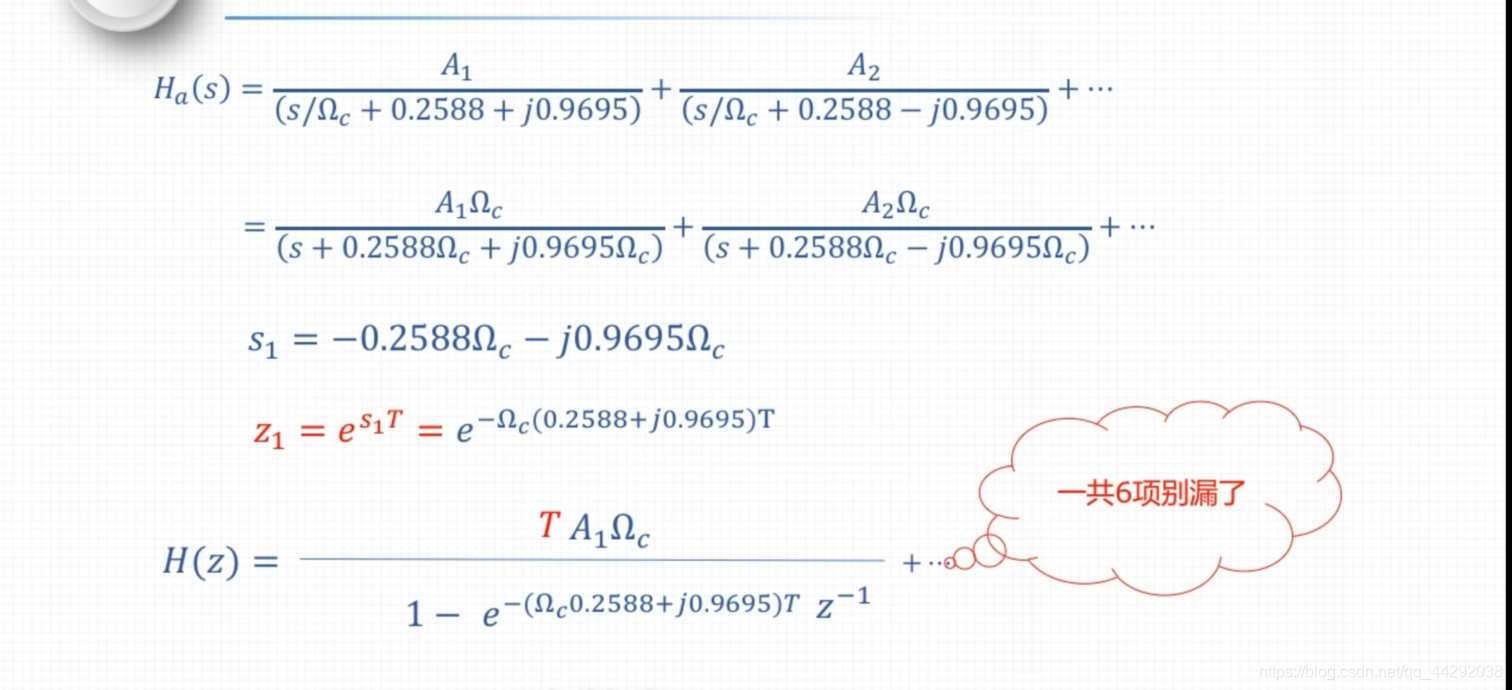
简单实例:
例2:设计IIR数字低通滤波器-双线性变换法


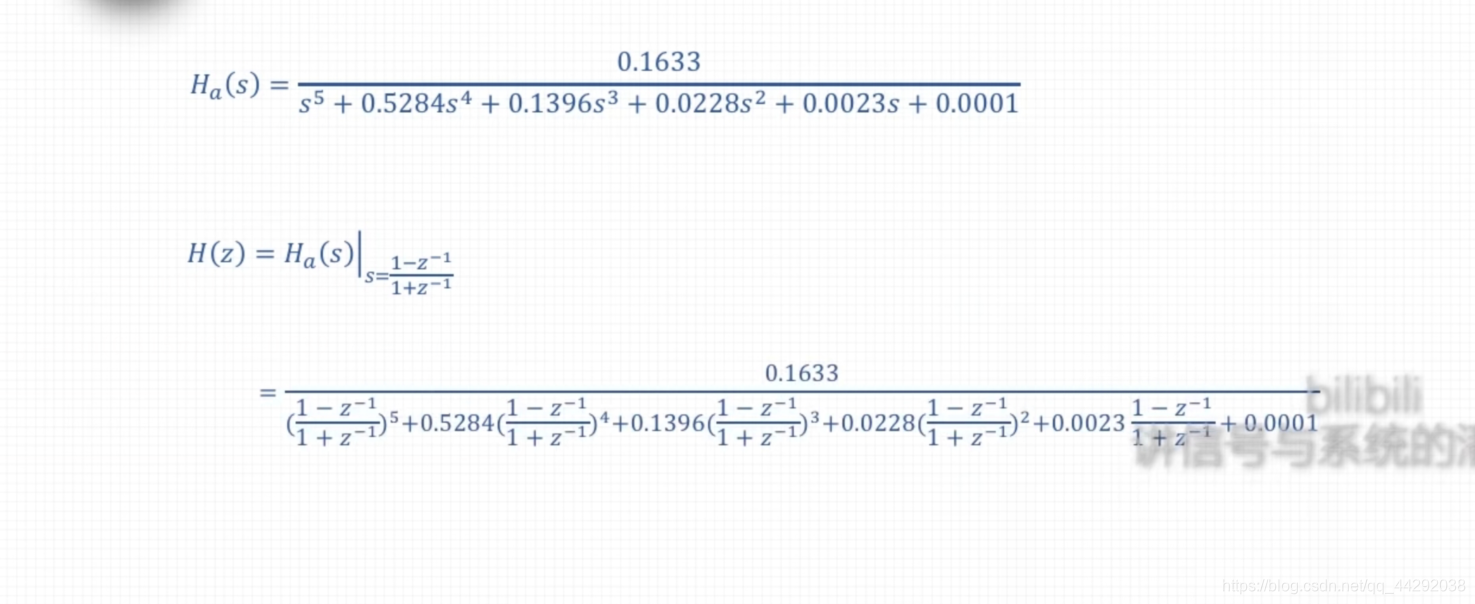
例3:设计IIR数字高通滤波器-双线性变换法(不能用脉冲响应不变法)




2.2 FIR滤波器设计
第一类线性相位:h(n)偶对称
频域特点:θ ( w ) = − τ w \theta(w)=-\tau wθ(w)=−τw
时域特点:h ( n ) 以 τ 为 中 心 偶 对 称 , τ = N − 1 2 , 即 h ( n ) = h ( N − 1 − n ) h(n)以\tau 为中心偶对称,\tau=\frac{N-1}{2},即h(n)=h(N-1-n)h(n)以τ为中心偶对称,τ=2N−1,即h(n)=h(N−1−n)
N为奇数时,对称轴有数值;N为偶数时,对称轴可以没有数值的小数
第二类线性相位:h(n)奇对称
频域特点:θ ( w ) = − π 2 − τ w \theta(w)=-\frac{\pi}{2}-\tau wθ(w)=−2π−τw
时域特点:h ( n ) 以 τ 为 中 心 奇 对 称 , τ = N − 1 2 , 即 h ( n ) = − h ( N − 1 − n ) h(n)以\tau 为中心奇对称,\tau=\frac{N-1}{2},即h(n)=-h(N-1-n)h(n)以τ为中心奇对称,τ=2N−1,即h(n)=−h(N−1−n)
N为奇数时,对称轴有数值且数值必须为0;N为偶数时,对称轴可以没有数值的小数
线性相位FIR滤波器幅度响应的特点(三角函数形式的傅里叶变换)
一类线性相位h(n)偶对称,N为奇数

一类线性相位h(n)偶对称,N为偶数(H ( π ) = 0 H(\pi)=0H(π)=0,不能高通、带阻)

二类线性相位h(n)奇对称,N为偶数 (H ( 0 ) = H ( π ) = 0 H(0)=H(\pi)=0H(0)=H(π)=0,不能低通、带阻、高通)
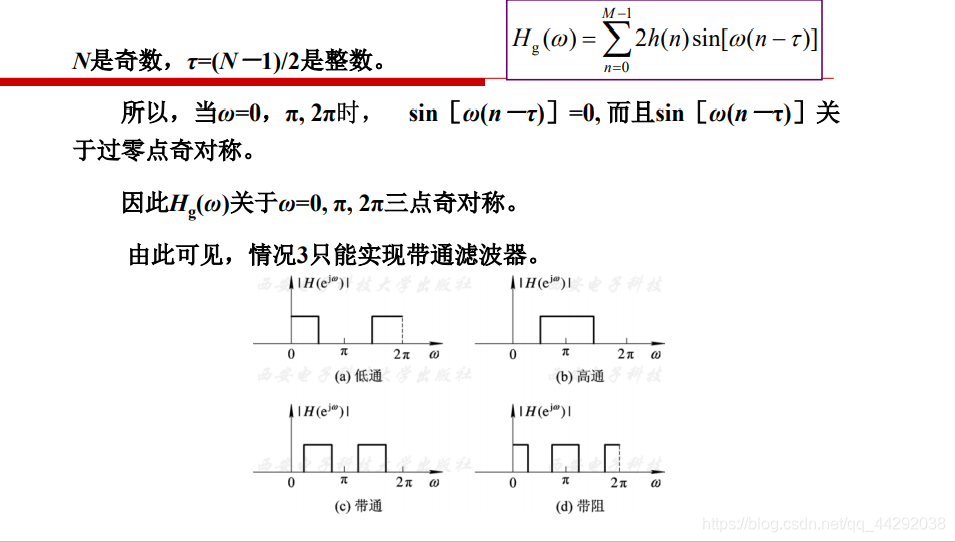
二类线性相位h(n)奇对称,N为奇数 (H ( 0 ) = 0 H(0)=0H(0)=0,不能低通、带阻)

窗函数法
目标滤波器的频域特性H d ( w ) H_d(w)Hd(w),对应目标滤波器的时域特性h d ( n ) h_d(n)hd(n)
对目标滤波器的时域特性做怎样的处理(选取怎样的窗函数w ( n ) w(n)w(n))
实际能实现滤波器的时域特性h ( n ) h(n)h(n),实际能实现滤波器的频域特性H ( w ) H(w)H(w)
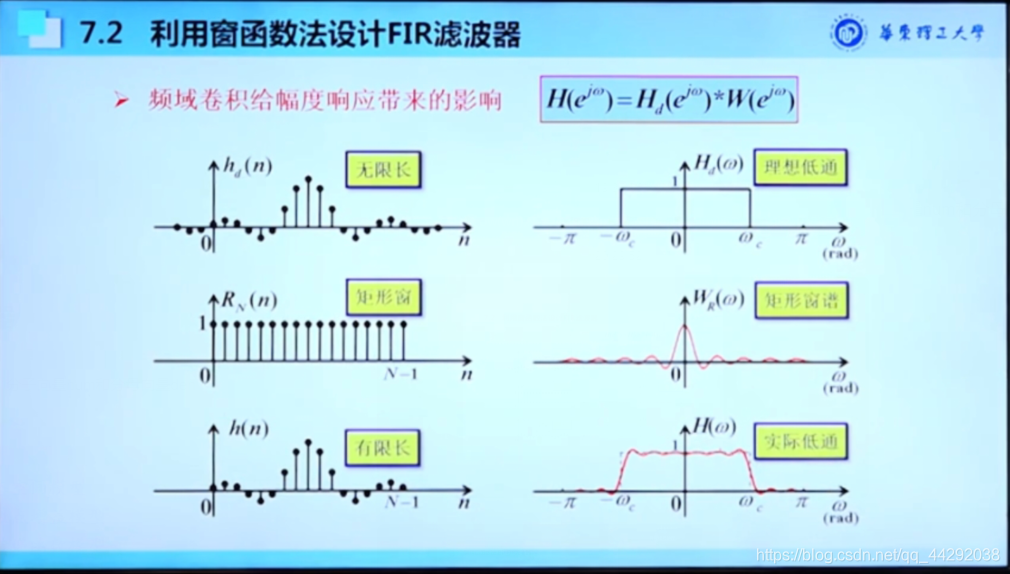
使用矩形窗的滤波器实际频域H(w)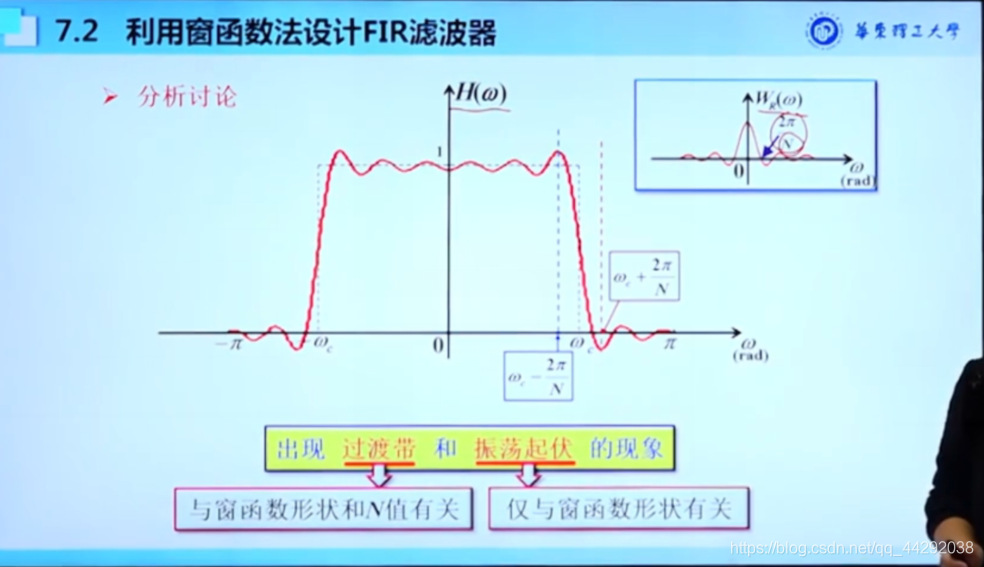
其他窗函数的时域w ( n ) w(n)w(n)表达式与频域H(w)图像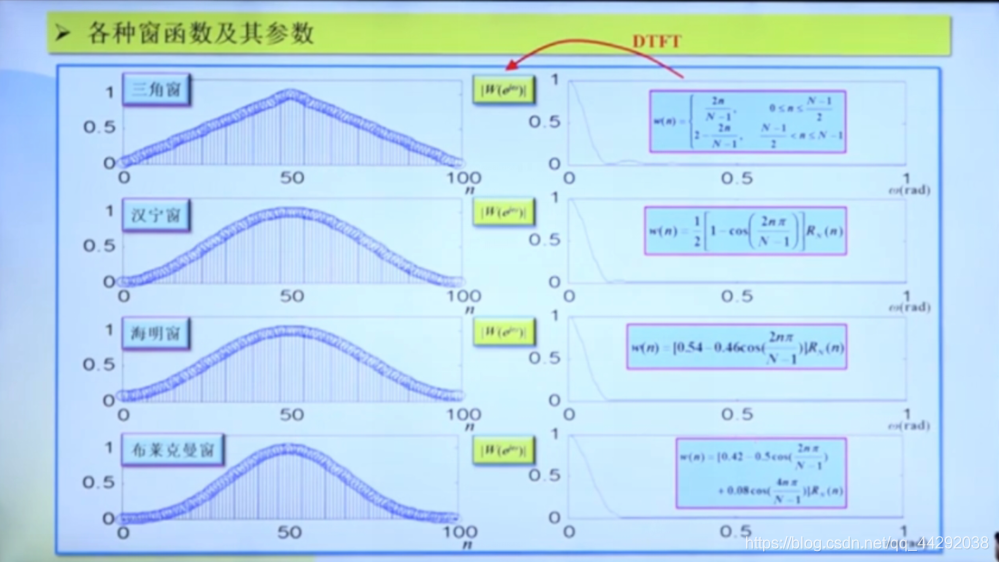
窗函数的技术指标:N越大W ( w ) 与 H ( w ) W(w)与H(w)W(w)与H(w)过渡带越窄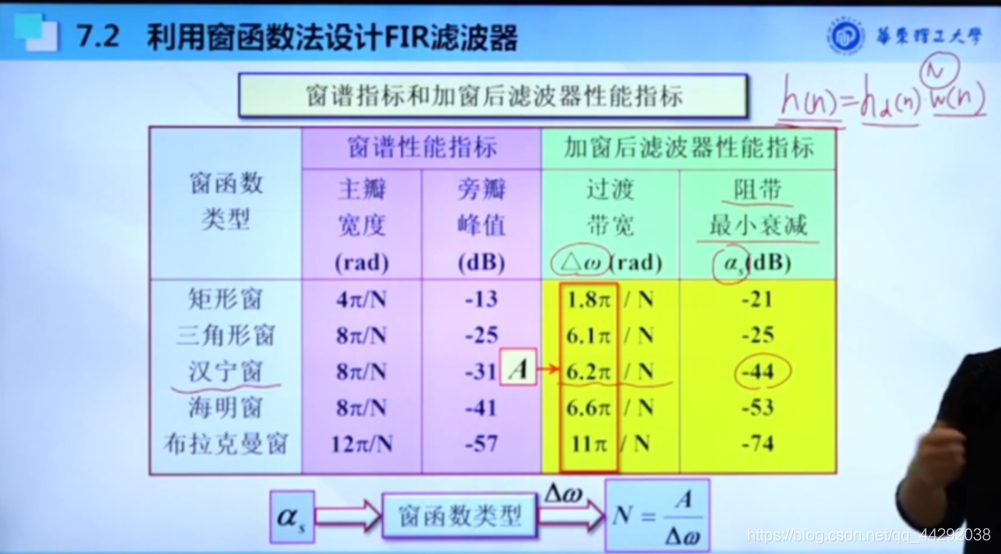
给定指标阻带最小衰减α s \alpha_sαs,找到衰减更厉害一些满足条件的窗的A
给定指标过渡带宽Δ w \Delta wΔw(通过条件计算出来)
N = A Δ w N=\frac{A}{\Delta w}N=ΔwA