贝塞尔曲线是在计算机图形学和相关领域内常用的一种参数曲线,它的主要应用有
生成光滑的曲线
动画
圆滑的字体,比如TrueType
它由一系列控制点P0到PN组成(n=1时是一阶,n=2时是2阶,etc),第一个和最后一个控制点总是曲线的终端节点,而中间的控制点通常不会出现在曲线上。
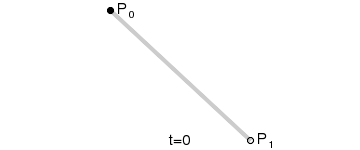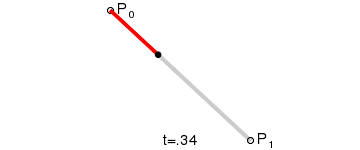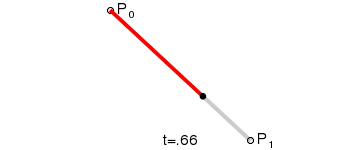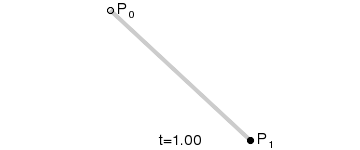
一阶贝塞尔曲线

它表示的点B随着t变化的位置如图所示:
二阶贝塞尔曲线
计算后得到:
它表示的点B随着t变化的位置如图所示
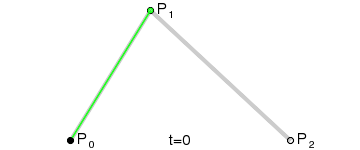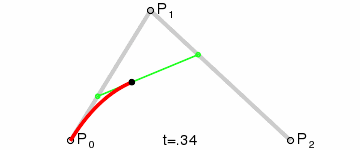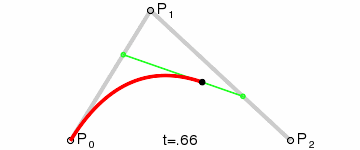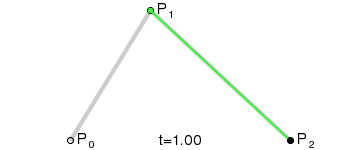
三阶贝塞尔曲线
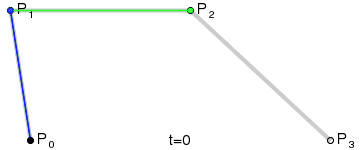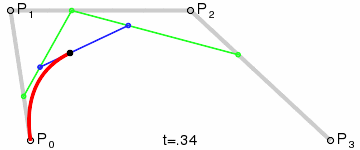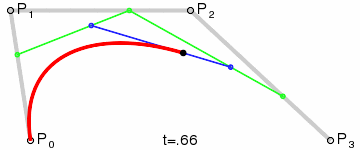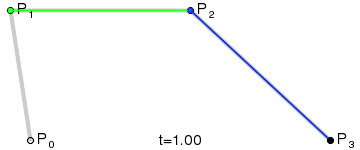
Android 中的Path类可以直接绘制一阶到三阶的贝塞尔曲线,在onDraw(Canvas canvas) 方法中使用,其中start,endpoint分别表示起始点和终点,一般也叫做数据点,controlPoint则是中间的控制点:
绘制一阶贝塞尔曲线:
1canvas.drawLine(start.x,start.y,end.x,end.y);
绘制二阶贝塞尔曲线:
1
2
3mPath.moveTo(startPoint.x, startPoint.y);//起点
mPath.quadTo(controlPoint1.x, controlPoint1.y, endPoint.x, endPoint.y);
canvas.drawPath(mPath, mPaint);
绘制三阶贝塞尔曲线:
1
2
3mPath.moveTo(startPoint.x, startPoint.y);//起点
mPath.cubicTo(controlPoint1.x, controlPoint1.y, controlPoint2.x, controlPoint2.y, endPoint.x, endPoint.y);
canvas.drawPath(mPath, mPaint);
当我们知道不在一条直线上的三个或者以上固定的点的时候,就可以利用api绘制出一条曲线,不过大多数的情况下,这三个点的坐标通常不是固定的,因此就可以不断地绘制一段一段连接起来的光滑的曲线,连续绘制的时候,quadTo或者cubicTo的终点就是下一段的起点。
因为网上已经有很多的例子了,这次先看这里,建议下载源码到Android Studio里面去看,这里主要是分析一下源码
二阶模拟和三阶模拟 :
没什么好说的,主要是基于控制点坐标的变化不断的重新绘制曲线,可以理解一下基础的变化。
圆滑绘图 :
里面的一段关键代码:
case MotionEvent.ACTION_MOVE:
float x1 = event.getX();
float y1 = event.getY();
float preX = mX;
float preY = mY;
float dx = Math.abs(x1 - preX);
float dy = Math.abs(y1 - preY);
if (dx >= offset || dy >= offset) {
// 贝塞尔曲线的控制点为起点和终点的中点
float cX = (x1 + preX) / 2;
float cY = (y1 + preY) / 2;
mPath.quadTo(preX, preY, cX, cY);
mX = x1;
mY = y1;
}
刚开始看的时候不是很理解为什么是mPath.quadTo(preX, preY, cX, cY),明明注释里面说控制点是(cX, cY),我们假设在绘图的时候有下面这种情形

mPath.quadTo(preX, preY, cX, cY) 第一次调用是时候,起始点控制点终点分别是AAD,这样子画出来是AD直线,第二次调用的时候起始点控制点终点则变成了DBE,然后就是ECF,实际上是以各个线段的中点作为数据点绘制的,这样子就把折线的角度改成了圆滑的曲线。
曲线变形
这里用到了属性动画
1
2
3
4
5
6
7
8
9
10
11mAnimator = ValueAnimator.ofFloat(mStartPointY, (float) h);
mAnimator.setInterpolator(new BounceInterpolator());
mAnimator.setDuration(1000);
mAnimator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() {
@Override
public void onAnimationUpdate(ValueAnimator valueAnimator) {
mAuxiliaryOneY = (float) valueAnimator.getAnimatedValue();
mAuxiliaryTwoY = (float) valueAnimator.getAnimatedValue();
invalidate();
}
});
从起点mStartPointY到屏幕底部h的一段属性动画,利用动画中y值的变化更新控制点的坐标
波浪动画
这里有个更详细的版本,对于
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
mPath.reset();
mPath.moveTo(-mWaveLength + mOffset, mCenterY);
for (int i = 0; i < mWaveCount; i++) {
// + (i * mWaveLength)
// + mOffset
mPath.quadTo((-mWaveLength * 3 / 4) + (i * mWaveLength) + mOffset, mCenterY + 60, (-mWaveLength / 2) + (i * mWaveLength) + mOffset, mCenterY);
mPath.quadTo((-mWaveLength / 4) + (i * mWaveLength) + mOffset, mCenterY - 60, i * mWaveLength + mOffset, mCenterY);
}
mPath.lineTo(mScreenWidth, mScreenHeight);
mPath.lineTo(0, mScreenHeight);
mPath.close();
canvas.drawPath(mPath, mPaint);
}
mPath.quadTo这个方法里面,需要明确的是虽然i是变化的,但实际上offset不变的时候,绘制出来的就是一条固定形状的曲线。从屏幕外面的左边一直绘制到屏幕外面的右边,当offset随着属性动画变化的时候,mPath.quadTo绘制的所需要的起始点控制点终点的x坐标都在以相同的大小增加,这样绘制出来的曲线也会随着平移,去除掉屏幕外面的部分,屏幕内显示的就是波浪动画了。
路径动画
这里算是真真正正用到了上面所提到的B(t)的求值公式。主要是重写了估值器,
1
2
3
4
5
6
7
8
9
10
11
12
13public class BezierEvaluator implements TypeEvaluator {
private PointF mControlPoint;
public BezierEvaluator(PointF controlPoint) {
this.mControlPoint = controlPoint;
}
@Override
public PointF evaluate(float t, PointF startValue, PointF endValue) {
return BezierUtil.CalculateBezierPointForQuadratic(t, startValue, mControlPoint, endValue);
}
}
其中3个控制点都固定了位置,正好插值器传过来的t的值[0,1],根据上面所提到的二阶贝塞尔的公式,就可以得到曲线上的点B(t)的值,然后返回给valueAnimator.getAnimatedValue(),把这个点变化的过程绘制出来就是贝塞尔曲线了。当把固定的小球,曲线都不绘制出来的时候,视觉效果就出来了。
切线拟合
纯数学。两个圆通过属性动画已经画出来,主要是一个圆的坐标变化导致的连接块的范围变化。
实现了两个简单的动画效果:

这个动画主要用到的知识是用四段三阶贝塞尔曲线去画一个圆,在这里和这里给出了绘制的思路,圆画出来之后,就是常规的改变控制点的位置来重绘曲线了,虽然这个动画挺简单的,不过三阶曲线去拟合一个圆,这个思路在后面很多的地方都会用到。
然后是这样一个心型上升动画
用来练练手。其实就是一个起点固定,两个控制点和终点都不固定的三阶贝塞尔曲线,不过需要注意的是因为添加了view,动画结束后需要remove掉。
代码上传到了github
感谢: