高斯函数曲线及简单积分

高斯函数曲线及简单积分

一、高斯函数的分布曲线

1. 高斯函数形式
   
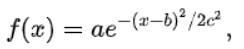
   其中a、b与c为实数常数，且a> 0。

2. 在统计学与概率论中，高斯函数是**正态分布**的密度函数；
   
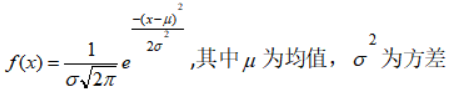
   服从N（μ，σ^2），期望值μ决定了其位置，标准差σ决定了分布的幅度；
   μ=0，σ^2=1为标准正态分布。

3.高斯函数的曲线图
function [out] = gauss(mean,sigma)
% gauss1 高斯函数曲线
% mean 均值， sigma方差
x=-10:0.0001:10;
y=(1/((sqrt(2*pi))*sigma))*exp(-((x-mean).^2)/(2*sigma.^2));
out=y;
plot(x,y,'LineWidth',1);
title('正态随机过程一维概率密度函数(高斯曲线)');
% legend(['均值=' num2str(mean)  ',标准差=' num2str(sigma)]);
 %num2str()应该是用来将数字类型转换成字符串的
 %中括号[]用来拼串
hold on
--------------------------------
gauss(0,1);
gauss(1,1);
gauss(1,2);
legend(['均值=0' ',标准差=1'],['均值=1' ',标准差=1'],['均值=1' ',标准差=2']);

（1）期望值μ决定了其位置，标准差σ决定了分布的幅度，随着μ增大，图的位置向右偏移；随着标准差σ增大，图的幅度降低。

（2）σ越小，分布越集中在μ附近，σ越大，分布越分散。

（3）关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。

（4）中间高两边低，图像是一条位于x轴上方的钟形曲线。

（5）曲线与横轴间的面积总等于1，相当于概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。

二、简单积分直角坐标系转换为极坐标系：
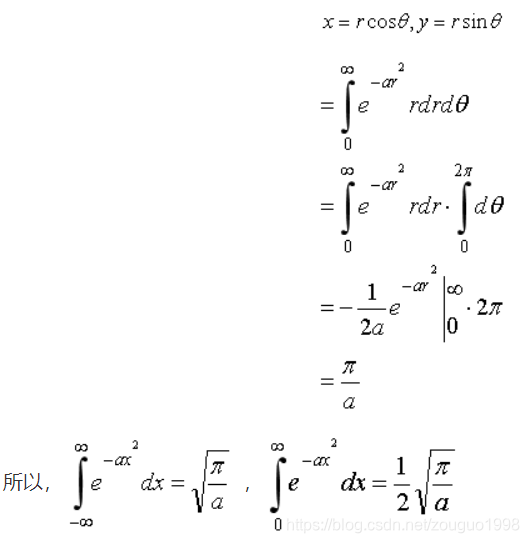
分析：坐标转换后有 r

参考： 正态分布曲线_百度百科 (baidu.com)

(1条消息) 推导为什么笛卡尔坐标与极坐标转换时，积分变量转换为 dxdy=ρdρdθ_Nancy_fairy的博客-CSDN博客